图
1.学习总结
1.1图的思维导图
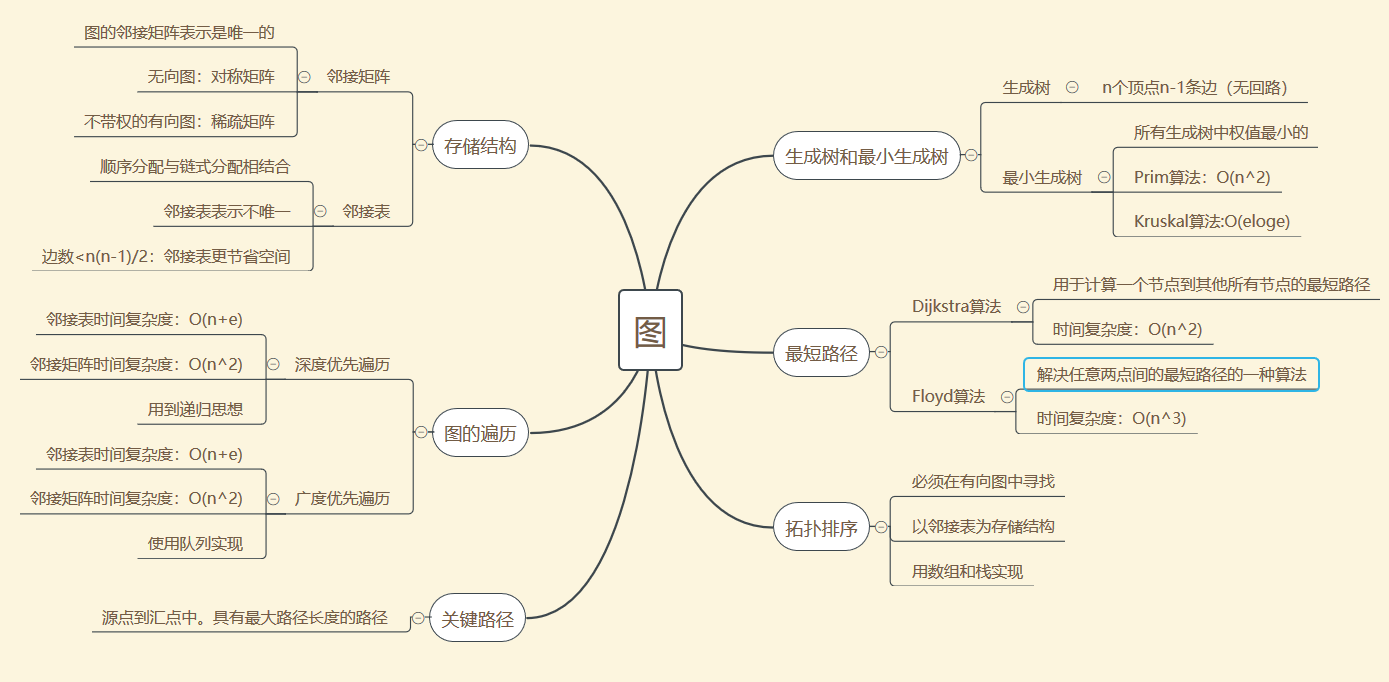
1.2 图结构学习体会
图的深度遍历算法是一个递归过程,广度遍历算法需用到队列操作
Prim和Kruscal算法都是求最小生成树的经典算法,Prim算法要多次寻找邻边的权重最小值,而Kruskal是先对权重排序后再进行查找。在算法效率上Kruskal要优于Prim,且代码更为简洁。
Dijkstra算法用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层扩展,直到扩展到终点为止。
拓扑排序算法用于在有向图中寻找拓扑序列,采用邻接表为存储结构。
2.PTA实验作业
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
使用图的邻接表存储结构,再顶点信息和边信息中加上一个变量存储颜色信息 先建图,完善图的信息 输入顶点颜色种类时,通过循环判断之前是否出现过相同颜色来计算颜色数量 若颜色数量与题目要求一致,再判断相邻顶点颜色是否相同 判断方法为:若头节点颜色与其某一nextarc节点颜色一致,则是非解 反之,若每一个头节点都与其所有的nextarc节点颜色不同,则是解
2.3 代码截图
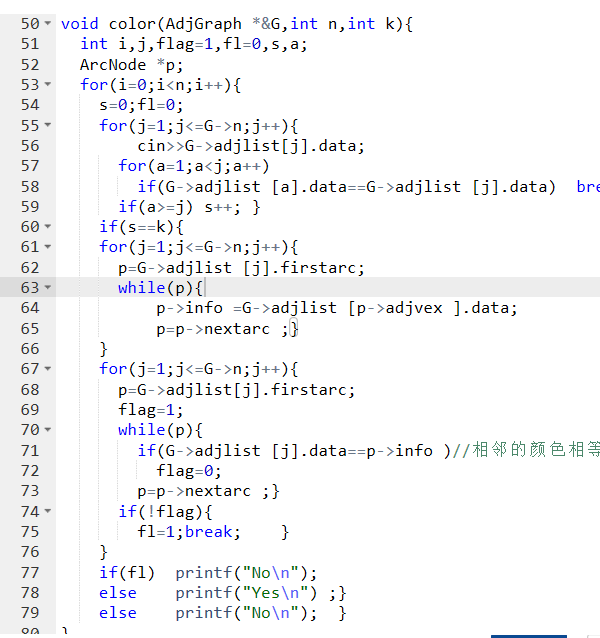
2.4 PTA提交列表说明。

第一次提交错误是因为输出的时候没有按题目要求,忽略了大小写的问题,还有就是最大图运行错误,设定的邻接表数组大小不够,第二次提交修正了大小写,第三次提交把数组最大值改大。
2.1 题目3:7-3 六度空间
2.2 设计思路(伪代码或流程图)
本题使用邻接表的存储方式和广度优先遍历算法 先建无向图,通过循环把每个节点都作为广度优先遍历的开始节点调用算法 定义变量计算广度遍历层数和节点数,每当遍历到每层的最后一个节点时,层数+1 遍历层数达到六层跳出循环并返回节点数
2.3 代码截图
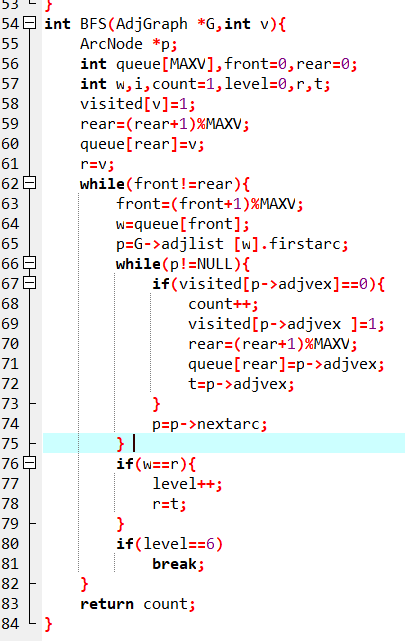
2.4 PTA提交列表说明
第一次输出的时候没有%,需要打%%才能输出,然后邻接表数组不够大,修改了一下MAXV值
2.1 题目2:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
本题主要是对最小生成树的简单应用
直接用数组实现,再对Prim算法稍加修改就行了
void prim(int cost[][MAXV],int n,int v){
定义lowcost数组和closest数组存放权值和顶点序号
给lowcost和closest数组置初值
for(i=1 to n-1){
min=inf;
for(j=1 to n-1){//找离v最近的顶点
if(边存在且权值小于min){
保存权值和终结点
count++;生成树边数+1
}
}
s=s+min;
lowcost[k]=0标记k已加入
修改lowcost和closest数组
}
if count<n 输出-1
else 输出s
}
2.3 代码截图
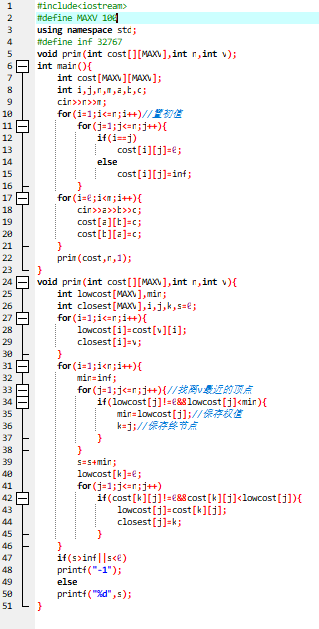
2.4 PTA提交列表说明。
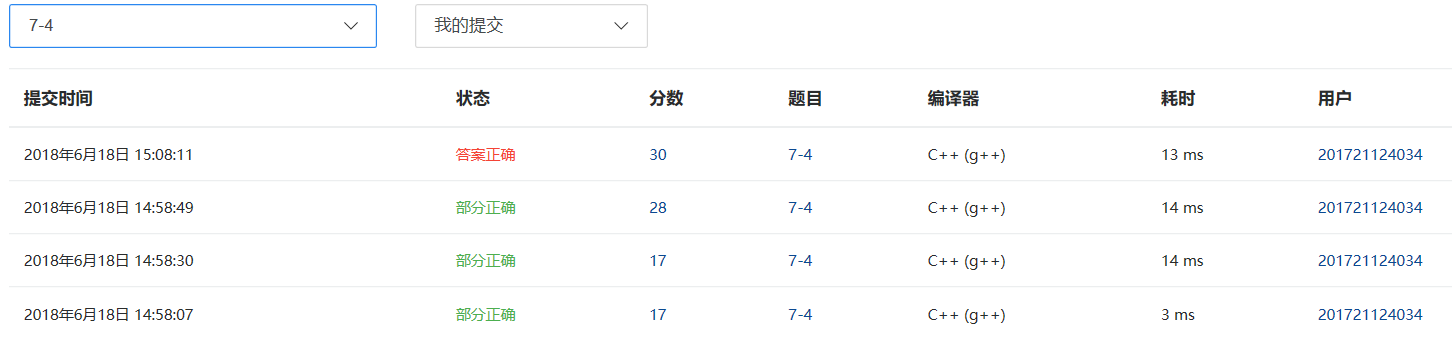
第一次和第二次提交都是因为最大N和M错误,数组范围不够大,然后是没有生成树时输出-1,忘了加上。
再定义一个变量统计已连通的边是否等于节点个数减1即可。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:250
4. 阅读代码
关键活动
假定一个工程项目由一组子任务构成,子任务之间有的可以并行执行,有的必须在完成了其它一些子任务后才能执行。“任务调度”包括一组子任务、以及每个子任务可以执行所依赖的子任务集。
比如完成一个专业的所有课程学习和毕业设计可以看成一个本科生要完成的一项工程,各门课程可以看成是子任务。有些课程可以同时开设,比如英语和C程序设计,它们没有必须先修哪门的约束;有些课程则不可以同时开设,因为它们有先后的依赖关系,比如C程序设计和数据结构两门课,必须先学习前者。
但是需要注意的是,对一组子任务,并不是任意的任务调度都是一个可行的方案。比如方案中存在“子任务A依赖于子任务B,子任务B依赖于子任务C,子任务C又依赖于子任务A”,那么这三个任务哪个都不能先执行,这就是一个不可行的方案。
任务调度问题中,如果还给出了完成每个子任务需要的时间,则我们可以算出完成整个工程需要的最短时间。在这些子任务中,有些任务即使推迟几天完成,也不会影响全局的工期;但是有些任务必须准时完成,否则整个项目的工期就要因此延误,这种任务就叫“关键活动”。
请编写程序判定一个给定的工程项目的任务调度是否可行;如果该调度方案可行,则计算完成整个工程项目需要的最短时间,并输出所有的关键活动。
输入格式:
输入第1行给出两个正整数N(≤100≤100)和M,其中N是任务交接点(即衔接相互依赖的两个子任务的节点,例如:若任务2要在任务1完成后才开始,则两任务之间必有一个交接点)的数量。交接点按1~N编号,M是子任务的数量,依次编号为1~M。随后M行,每行给出了3个正整数,分别是该任务开始和完成涉及的交接点编号以及该任务所需的时间,整数间用空格分隔。
输出格式:
如果任务调度不可行,则输出0;否则第1行输出完成整个工程项目需要的时间,第2行开始输出所有关键活动,每个关键活动占一行,按格式“V->W”输出,其中V和W为该任务开始和完成涉及的交接点编号。关键活动输出的顺序规则是:任务开始的交接点编号小者优先,起点编号相同时,与输入时任务的顺序相反。
输入样例:
7 8
1 2 4
1 3 3
2 4 5
3 4 3
4 5 1
4 6 6
5 7 5
6 7 2
输出样例:
17
1->2
2->4
4->6
6->7
#include <stdio.h>
#include<stdlib.h>
struct data
{
int b,lenth;
};
typedef struct node *Node;
struct node
{
struct data Next[101];
int Output,O;
struct data From[101];
int Input,I;
};
int TopSort(Node V,int n);
int* ImportantRode(Node,int,int );
int main()
{
struct node V[101];
int n,m;
scanf("%d%d",&n,&m);
for(int i=1; i<=n; i++)
{
V[i].Input =0;
V[i].Output =0;
}
while(m--)
{
int disk1,disk2,lenth;
scanf("%d%d%d",&disk1,&disk2,&lenth);
V[disk1].Next[++V[disk1].Output].b =disk2;
V[disk1].Next[V[disk1].Output ].lenth=lenth;
V[disk2].From[++V[disk2].Input].b=disk1;
V[disk2].From[V[disk2].Input].lenth=lenth;
}
for(int i=1;i<=n;i++){
V[i].I =V[i].Input ;
V[i].O=V[i].Output ;
}
int Coast =TopSort(V,n);
return 0;
}
int TopSort(Node V,int n)
{
int Earliest[101]= {0};
while(1)
{
int flag=0;
for(int i=1; i<=n; i++)
{
if(0==V[i].Input)
{
// printf("{%d}",i);
flag=1;
for(int j=1; j<=V[i].Output ; j++)
{
if(Earliest[V[i].Next[j].b]<Earliest[i]+V[i].Next[j].lenth)
{
Earliest[V[i].Next[j].b]=Earliest[i]+V[i].Next[j].lenth;
}
V[V[i].Next[j].b].Input-=1;
}
V[i].Input =-1;
}
}
if(!flag)break;
}
// for(int i=0;i<n;i++){
// printf("[%d|%d->%d]",V[i].Input,V[i].Output,Earliest[i] );
// }
int max=0,index;
for(int i=1; i<=n; i++)
{
if(V[i].Input >0)
{
max=0;
break;
}
if(Earliest[i]>max)
{
max=Earliest[i];
index=i;
}
}
printf("%d",max);
if(max==0)return 0;
int *Latest=ImportantRode(V,max,n);
for(int i=1; i<=n; i++)
{
// printf("{%d,%d}",Earliest[i],Latest[i]);
if(Latest[i]==Earliest[i])
{
for(int j=V[i].O; j>0; j--)
{
if(Latest[V[i].Next[j].b]==Latest[i]+V[i].Next[j].lenth )
{
printf("\n%d->%d",i,V[i].Next[j].b);
}
}
}
}
return max;
}
int* ImportantRode(Node V,int max,int n)
{
int*Latest=(int*)malloc(sizeof(int)*101);
for(int i=1; i<=n; i++)
{
Latest[i]=max;
}
while(1)
{
int flag=0;
for(int i=1; i<=n; i++)
{
if(0==V[i].Output)
{
flag=1;
for(int j=1; j<=V[i].I; j++)
{
if(Latest[V[i].From[j].b]>Latest[i]-V[i].From[j].lenth)
{
Latest[V[i].From[j].b]=Latest[i]-V[i].From[j].lenth;
}
V[V[i].From[j].b].Output -=1;
}
V[i].Output =-1;
}
}
if(!flag)break;
}
return Latest;
}



