并查集(进阶)
一、引文
上一篇博客——并查集(入门)写完后,我对并查集有了基本的了解。
- 并查集可以判断一幅无向图中有几个连通分量
- 并查集的find、join函数都是必不可少的
- 路径压缩算法对于并查集的优化也很关键
有了这些知识,我成功AC了hdu1232畅通工程,总觉得并查集不应该这么简单(套模板,修改一点点就AC),后来,遇到了poj1182食物链这道题,发现只学习了上篇博客的知识是无法解决它的,是时候增加自己的知识量了。
二、正文
- 并查集的进阶主要内容是解决带权并查集的相关问题。
- 在原有并查集的基础上,加入集合内部元素和其父节点之间的关系,这样的拓展,可以解决更多问题
- 带权并查集和普通并查集最大的区别在于带权并查集合并的是可以推算关系的点的集合(可以通过集合中的一个已知值推算这个集合中其他元素的值)。而一般并查集合并的意图在于这个元素属于这个集合。带权并查集相当于把“属于”的定义拓展了一下,拓展为有关系的集合。
来看这么一道题目:警察抓获N个罪犯,这些罪犯只可能属于两个黑帮团伙中的一个,现在给出M个条件(D a b表示a和b不在同一团伙),对于每一个询问(A a b)确定a,b是不是属于同一黑帮团伙或者不能确定。
之前的解题观点:D a b表示a和b不在同一个团伙??我们平时碰到的不都是两人在同一个团伙,然后用unite函数将两人放入同一个连通分支内。所以这道题给我的第一印象是将两个团伙看作两个连通分支,然后将相应的罪犯加入到相应的连通分支中,最后要询问时,只要判断两个罪犯的祖先是否一致(如果一致,那么两人是同一团伙)。
不可行的地方:D a b只表明a和b不属于同一个连通分支,并没有明确说明a和b属于哪个团伙(设想一下,如果说明了,那岂不是so easy),那么该怎么办呢?
新思路:仔细想想,我们是否可以存储每个节点与其祖先的关系。拿这道题来说,我们用一维数组r[]存储每个节点与其祖先是否属于同一团伙(例如r[x]=0表示结点x与其祖先属于同一团伙,而r[x]=1则表示结点x与其祖先不属于同一团伙)。有了这个关系尚且不够,我还有一些疑惑,这个祖先是谁哇?这个关系是怎么得出的哇?
继续前进:对于这题每次输入的D a b,我们都知道a和b不属于同一团伙,也就是a和b不在同一连通分支。而我们要做的是将a和b归于同一个祖先之下(即连接a和b所在的连通分支),伴随这一操作的还有更新r[a]、r[b](怎么更新稍后谈),为何要将a和b归于同一个连通分支呢?因为后面的查询A a b,我们通过判断find(a)==find(b)是否成立来确定我们是否知道他们的关系(成立就说明他们属于同一连通分支,说明他们已经D a b过了,不成立就可以输出"Not sure yet."啦),在find(a)==find(b)成立的情况下,我们就可以通过判断r[a]==r[b]是否成立来确定他们的具体关系(成立就说明他们属于同一团伙,就可以输出"In the same gang.",不成立就说明他们不属于同一个团伙,就可以输出"In different gangs.")。我们应该要知道上面那个式子r[a]==r[b]等价于r[a]==r[b]==0或r[a]==r[b]==1,即a和b如果属于同一团伙,暗含着他们与他们的祖先在同一个团伙或不在同一个团伙。读到这,我们并没有理清祖先是谁,关系怎么得出,但我们知晓了我们努力的目标。
于是,我们敲出了下面的代码:
if(a和b属于同一连通分支){
if(a和祖先的关系==b和祖先的关系){
cout<<"a和b属于同一团伙"<<endl;
}
else{
cout<<"a和b不属于同一团伙"<<endl;
}
}
else{
cout<<"还没有确定a和b的关系"<<endl;
}
再往前迈进:既然每次D a b都将a和b连起来,而且最后形成的那有且仅有一个的连通分支是由每次D a b的a和b结点组成,于是我们就可以确定祖先结点就是第一次D a b的a或b(具体是a还是b要看你的unite函数怎么写的了),后面我们才慢慢这个连通分支上再添加结点的。祖先节点我们搞懂了,再来搞懂关系即可。
最后一根稻草:我们前面说过数组r[x]表示节点x与根节点的关系,我们知道初始的时候,每个点都是一个连通分支(都有pre[i]=i,r[i]=0),而我们在构建一个由多个节点组成的连通分支时,我们新加入的节点的祖先在此刻发生变化,那么他们的r[]也要变化,当然,这是每次D a b出现后,将a和b所在的连通分支连起来时对r[]的更新,也就是在unite函数内的更新。此外,在find函数寻找根结点的时候也要不断更新r[](为啥啊为啥啊),因为unite函数内的r[]更新是在联合两棵树的时候进行的更新两棵树的根的关系,而其中相关子结点却未曾更新,所以要在find函数内进行更新(这样才能判断r[a]==r[b]是否成立)。下面,我们先解释find函数内r[]是怎么更新的,再解释unite函数内r[]是怎么更新的。
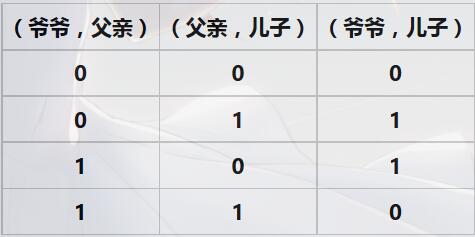
我们先解释:根据子节点a与父亲节点b的关系r1和父节点b与爷爷节点c的关系r2推导子节点a与爷爷节点c的关系r3
很容易通过穷举发现其关系式:a 和 b 的关系为 r1, b 和 c 的关系为r2,则 a 和 c 的关系r3为: r3 = ( r1 + r2) % 2; //(PS:因为只用两种情况所以对 2 取模)
于是find函数变为:
int find(int x) //找根节点
{
if(x == pre[x]) return x;
int t = pre[x]; //记录父亲节点 方便下面更新r[]
pre[x] = find(pre[x]);
r[x] = (r[x]+r[t])%2; //根据子节点与父亲节点的关系和父节点与爷爷节点的关系,推导子节点与爷爷节点的关系
return pre[x]; //容易忘记
}
在find函数内,若我们如此调用find(a),那么find函数除了返回a的祖先,还会在这过程中确定r[a]的值(即a与祖先结点的关系)。
最后,我们再来解释unite函数内的r[]更新:
定义:fx 为 x的根节点, fy 为 y 的根节点,联合时,使得 pre[fx] = fy (即fy也变为x和fx的祖先)
同时也要寻找 fx 与 fy 的关系(此时fy是fx的祖先),于是有 r[fx] = (r[x]+r[y]+1)%2
证明过程:fx 与 x 的关系是 r[x], x 与 y 的关系是 1 (因为确定是不同类,才联合的),y与 fy 关系是 r[y],模 2 是因为只有两种关系,所以又上面的一点所推出的定理可以证明 fx 与 fy 的关系是: (r[x]+r[y]+1)%2
于是unite函数变为:
void unite(int x, int y)
{
int fx = find(x); //x所在集合的根节点
int fy = find(y);
pre[fx] = fy; //合并
r[fx] = (r[x]+1+r[y])%2; //fx与x关系 + x与y的关系 + y与fy的关系 = fx与fy的关系
}
有了以上的详细分析,代码怎么敲不用讲了吧。哈哈。还是贴上一个AC代码,仅供参考。

#include<cstdio> #include<iostream> using namespace std; const int maxn = 100000+10; int pre[maxn]; //存父亲节点 int r[maxn]; //存与根节点的关系,0 代表同类, 1代表不同类 int T,n,m; void init() { for(int i=1;i<=n;i++){ pre[i] = i; r[i] = 0; } } int find(int x) { if(x == pre[x]) return x; int t = pre[x]; pre[x] = find(pre[x]); r[x] = (r[x]+r[t])%2; return pre[x]; } void unite(int x,int y) { int fx = find(x); int fy = find(y); pre[fx] = fy; r[fx] = (r[x]+1+r[y])%2; } int main() { scanf("%d",&T); while(T--){ scanf("%d%d",&n,&m); init(); int a,b; char ch; while(m--){ getchar(); scanf("%c%d%d",&ch,&a,&b); if(ch == 'D'){ unite(a,b); } else{ if(find(a) == find(b)){ if(r[a] == r[b]){ cout<<"In the same gang.\n"; } else{ cout<<"In different gangs.\n"; } } else{ cout<<"Not sure yet.\n"; } } } } return 0; }
上面那道题只是带权并查集中的种类并查集的一道开胃小菜,接下来我们来谈poj1182食物链这道题。
啊!!!我又做到一条和上面poj1073类似的题目,一块讲了,再讲poj1182吧。
题意:给定n只虫子,不同性别的可以在一起,相同性别的不能在一起。给你m对虫子,判断中间有没有同性别在一起的。
因为刚刚做完了上道题,这道题一看到,就有了思路。没得到一对虫子,我们就判断它们是否属于同一连通分支,如果是,我们再判断它们各自与根结点的性别是否相同,如果两个性别都与根结点的性别相同,说明这一对虫子的性别相同,答案就出来了。
具体程序只要稍稍修改一下上面的代码即可。
说是如此说,我看到一个人的题解上写的r[x]表示的是x和父节点的关系(而不是和根结点),具体为r[x] = 0表示x和父节点关系为同性,r[x] = 1表示x和父节点关系为异性。
但是我测试了一下,仅改动这个定义而不该懂其他代码仍然AC。这说明或者我们前面的定义有问题或者这个定义有问题。话不多说,慢慢斟酌,先上这个代码。

#include <cstdio> #include <cstring> #include <cstdlib> using namespace std; #define maxn 5005 int T,n,m; int pre[maxn]; //记录父节点 int r[maxn]; //r[x]记录x和父节点之间的关系 //其中r[x] = 0表示x和父节点关系为同性, r[x] = 1表示x和父节点关系为异性 void init() { for(int i=1;i<=n;i++){ pre[i] = i; r[i] = 0; } } //集合查找 int find(int x) { if(pre[x] == x) return x; int t = pre[x]; pre[x] = find(t); r[x] = (r[x] + r[t]) % 2; //根据老的父节点和新父节点关系,修改r[x]值 return pre[x]; } //合并集合 void unite(int x, int y) { int fx = find(x); int fy = find(y); pre[fx] = fy; r[fx] = ((r[x] - r[y] + 1) % 2); //唯一一处不同的换成 r[fx] = ((r[x] + r[y] + 1) % 2); 还是AC } int main() { scanf("%d", &T); int kase = 1; while(T--) { scanf("%d%d", &n, &m); init(); int a,b,flag = 0; while(m--) { scanf("%d%d", &a, &b); if(find(a) == find(b)) { if(r[a] == r[b]) //如果不满足异性关系,有矛盾 flag = 1; } else { unite(a, b); } } printf("Scenario #%d:\n",kase++); if(flag==1) printf("Suspicious bugs found!\n\n"); else printf("No suspicious bugs found!\n\n"); } return 0; }
好啦好啦,不管是与父亲结点还是祖先结点的关系,咱们都直接进入poj1182食物链吧。
题意:三类动物A、B、C构成食物链循环,告诉两个动物的关系(同类或天敌),判断有多少个关系是和正确的冲突。
哈哈,看到这道题,一下子就注意到三类动物,之前我们研究的是两类,现在只是多了一类而已,真的是而已吗?
显然不是,如果我们依照上面的想法做,每来一对动物a b就将他们归于同一个祖先下,最后,只剩下一个连通分支。如果我们仍然设r[x]表示x与根结点的关系,那么就有r[x]=0表示与根结点同类,r[x]=1表示与根结点异类(???貌似有三个类啊??这样无法区分另外两个类啊)。
既然之前的想法不能解决问题,我们回本溯源,带权并查集的本质不就是多了各结点之间的关系吗?不妨大胆设一些关系。
想着想着,因为每来一句话都要判断其真假,所以必须要让所有结点在一个连通分支内(如果分3个分支,来了新的一对动物让你判断,如果发生前后矛盾,你将不知道是之前是错的还是现在的是错的),所以数组r[]要保留,既然是食物链,不妨设r[x]=0表示x与根结点同类,r[x]=1表示x吃根结点,r[x]=-1表示x被根结点吃。这样如果命令是1 a b时,我们便可以先判断它们是否是同一连通分支的,如果是,就判断它们各自与根结点的关系(即r[a]==r[b]),如果r[a]==r[b](即表示它们是同类),命令正确,反之说明这个命令是假话。当然,如果它们不是同一连通分支的,它们之间的关系就不好判定,命令真假也就无法确定,我们只能将两个点连入同一连通分支,即直接调用unite函数。如果命令是2 a b时(即a吃b),我们仍然先判断它们是否是同一连通分支的,如果是,我们可以穷举r[a]和r[b]的值来判断此话是否正确(若想命令正确只能是:r[a]=1,r[b]=0或r[a]=0,r[b]=-1或r[a]=-1,r[b]=1)。当然,如果不是同一连通分支的,同上,直接调用unite函数。
于是,我们可以得出下面的代码:
cin>>D>>a>>b;
if(D==1){
if(find(a) == find(b)) //a和b属于同一连通分量
if(r[a] != r[b]) //a和祖先的关系 与 b和祖先的关系 不一致
假话数量++; //即a和b的种类不一样
else
unite(a,b);
}
if(D==2){
if(find(a)==find(b))
if(不是正确的对应关系)
假话数量++;
else
unite(a,b);
}
看到这,我们目标就有啦啦啦!!至于关系的得到就锁定在find函数和unite函数内了,详细的推导日后再说。
我怀着自信满满的心去编程,却发现有个地方忽视了。。。当命令D a b过来时,如果a和b属于同一连通分支还好说,如果不是,我们就要unite(a,b),但是unite的具体内容决定r[]的更新,所以与当前传入的D有关。
于是,得到下面的代码:
cin>>D>>a>>b;
int sum = 0; //假话数量
if(a>n || b>n || (D==2&&x==y)) //如果节点编号大于最大编号,或者自己吃自己,说谎
sum++;
else if(find(a) == find(b)){
if(D==1 && r[a]!=r[b]) //如果 x 和 y 不属于同一类
sum++;
if(D==2 && (r[a]+1)%3!=r[b]) //如果a没有吃b(注意要对应unite(x,y)的情况,否则一路WA到死啊!!!)
sum++;
}
else{
unite(a,b,d); //如果开始没有关系,则建立关系
}
于是相应的代码就有了:

#include<cstdio> #include<iostream> using namespace std; const int maxn = 50000+10; int pre[maxn]; //存父亲节点 int r[maxn]; //存与根节点的关系 //r[x]==0表示x与根结点同种类 r[x]==1代表x会被根结点吃 r[x]==2代表x会吃根结点 int n,k; void init() { for(int i=1;i<=n;i++){ pre[i] = i; r[i] = 0; //初始每个动物都与自己同种类 } } int find(int x) { if(x == pre[x]) return x; int t = pre[x]; pre[x] = find(pre[x]); //回溯由子节点与父节点的关系和父节点与根节点的关系找子节点与根节点的关系 r[x] = (r[x]+r[t])%3; //此处模3 return pre[x]; } void unite(int x,int y,int d) { int fx = find(x); int fy = find(y); pre[fy] = fx; //合并树 注意:被x吃,所以以 x的根为父 r[fy] = (r[x]-r[y]+3+(d-1))%3; //对应更新与父节点的关系 } int main() { cin>>n>>k; init(); int sum = 0,D,a,b; while(k--){ scanf("%d%d%d",&D,&a,&b); if(a>n || b>n || (a==b&&D==2)){ sum++; continue; } else if(find(a) == find(b)) //如果原来有关系,也就是在同一棵树中,那么直接判断是否说谎 { if(D == 1 && r[a] != r[b]) sum++; //如果a和b不属于同一类 if(D == 2 && (r[a]+1)%3 != r[b]) sum++; // 如果a没有吃b (注意要对应unite(a,b)的情况,否则一路WA到死啊!!!) } else unite(a,b,D); //如果开始没有关系,则建立关系 } printf("%d\n",sum); return 0; }
写到这,只缺一些关系的证明了。我也不想证,怎么办??搬点别人的货吧。
—————————————————————————————食物链别人讲解————————————————————————————————
思路:把确定了相对关系的节点放在同一棵树中
每个节点对应的 r[]值记录他与根节点的关系:
0:同类,
1:被父亲节点吃,
2: 吃父亲节点
每次输入一组数据 d, x, y判断是否超过 N 后,先通过find()函数找他们的根节点从而判断他们是否在同一棵树中。(也就是是否有确定的关系)
1.如果在同一棵树中find(x) == find(y):直接判断是否说谎。
1)如果 d ==1,那么 x 与 y 应该是同类,他们的r[]应该相等
如果不相等,则说谎数 +1
2)如果 d==2,那么 x 应该吃了 y,也就是 (r[x]+1)%3 == r[y]
如果不满足,则说谎数 +1
如何判断 x 吃了 y 是 (r[x]+1)%3 == r[y],请看下图:(PS:箭头方向指向被吃方)
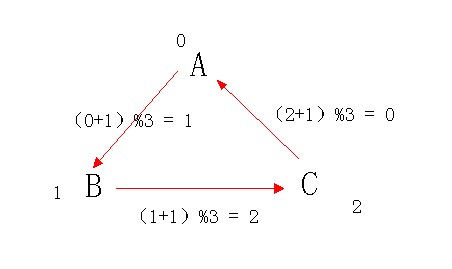
2.如果不在同一棵树中:那么合并 x 与 y 分别所在的树。
合并树时要注意顺序,我这里是把 x 树的根当做主根,否则会
WA的很惨
注意:找父亲节点时,要不断更新 r[]的值。
这里有一个关系:如果 x 和y 为关系 r1, y 和 z 为关系 r2
那么 x 和z的关系就是 (r1+r2)%3
如何证明?
无非是3*3 = 9种情况而已
(a, b) 0:同类 、 1:a被b吃 、 2:a吃b
|
(x, y) |
(y, z) |
(x,z) |
如何判断 |
|
0 |
0 |
0 |
0+0 = 0 |
|
0 |
1 |
1 |
0+1 = 1 |
|
0 |
2 |
2 |
0+2 = 2 |
|
1 |
0 |
1 |
1+0 = 1 |
|
1 |
1 |
2 |
1+1 = 2 |
|
1 |
2 |
0 |
(1+2)%3 = 0 |
|
2 |
0 |
2 |
2+0 = 2 |
|
2 |
1 |
0 |
(2+1)%3 = 0 |
|
2 |
2 |
1 |
(2+2)%3 = 1 |
关于合并时r[]值的更新:
如果 d == 1则 x和y 是同类 ,那么 y 对 x 的关系是 0
如果 d == 2 则 x 吃了 y, 那么 y 对 x 的关系是 1, x 对 y 的关系是 2.
综上所述 ,无论 d为1 或者是为 2, y 对 x 的关系都是 d-1
定义 :fx 为 x 的根点, fy 为 y 的根节点
合并时,如果把 y 树合并到 x 树中
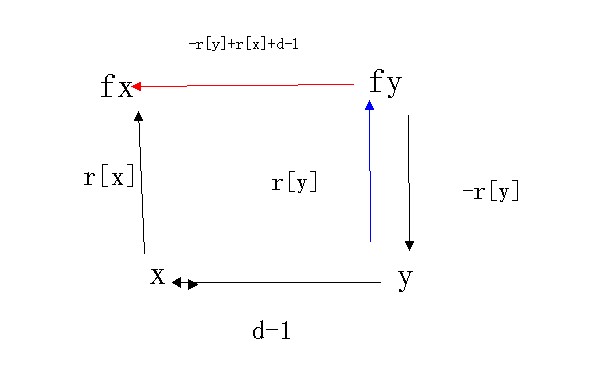
如何求 fy 对 fx 的r[]关系?
fy 对 y 的关系为 3-r[y]
y 对 x 的关系为 d-1
x 对 fx 的关系为 r[x]
所以 fy 对 fx 的关系是(3-r[y] + d-1 + r[x])%3
到这,带权并查集也告一段落了。并查集的学习给我的学习方法带来了不小的收获,一个解题过程的形成至关重要,先确定目标模板,然后思路就有了。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号