数据结构2——线段树
一、相关介绍
线段树:它在各个节点保存一条线段(数组中的一段子数组),主要用于高效解决连续区间的动态查询问题。由于二叉结构的特性,它基本能保持每个操作的复杂度为O(logn)。
线段树的每个节点表示一个区间,子节点则分别表示父节点的左右半区间,例如父亲的区间是[a,b],那么(c=(a+b)/2)左儿子的区间是[a,c],右儿子的区间是[c+1,b]。
下面我们从一个经典的例子来了解线段树,问题描述如下:
从数组arr[0...n-1]中查找某个(子)数组内的最小值,其中数组大小固定,但是数组中的元素的值可以随时更新。
- 对这个问题一个简单的解法是:遍历数组区间找到最小值,时间复杂度是O(n),额外的空间复杂度O(1)。当数据量特别大,而查询操作很频繁的时候,耗时可能会不满足需求。
- 另一种解法:使用一个二维数组来保存提前计算好的区间[i,j]内的最小值,那么预处理时间为O(n2),查询耗时O(1), 但是需要额外的O(n2)空间,当数据量很大时,这个空间消耗是庞大的,而且当改变了数组中的某一个值时,更新二维数组中的最小值也很麻烦。
我们可以用线段树来解决这个问题:预处理耗时O(n),查询、更新操作O(logn),需要额外的空间O(n)。
根据这个问题我们构造如下的二叉树:
- 叶子节点是原始数组array中的元素
- 非叶子节点代表它的(即此非叶子节点的)所有子孙叶子节点所在区间的最小值
例如对于数组[2, 5, 1, 4, 9, 3]可以构造如下的二叉树(背景为白色表示叶子节点,非叶子节点的值是其对应数组区间内的最小值,例如根节点表示数组区间array[0...5]内的最小值是1):
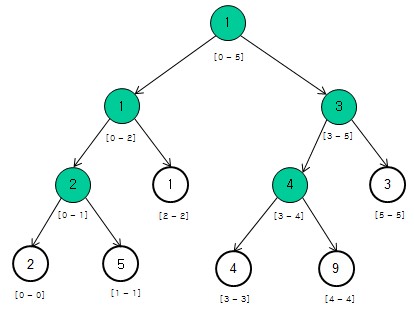
由于线段树的父节点区间是平均分割到左右子树,因此线段树是完全二叉树,对于包含n个叶子节点的完全二叉树,它一定有n-1个非叶节点,总共2n-1个节点,因此存储线段是需要的空间复杂度是O(n)。
二、算法实现
那么线段树的操作:创建线段树、查询、节点更新是如何运作的呢(以下所有代码都是针对求区间最小值问题)?
- 创建线段树
对于线段树我们可以选择和普通二叉树一样的链式结构。由于线段树是完全二叉树,我们也可以用数组来存储,下面的讨论及代码都是数组来存储线段树,节点结构如下(注意到用数组存储时,有效空间为2n-1,实际空间却不止这么多,比如上面的线段树中叶子节点1、3虽然没有左右子树,但是的确占用了数组空间,实际空间是满二叉树的节点数目,准确地讲,实际空间应设为4n):
struct SegTreeNode{
int val;
};
定义包含n个节点的线段树SegTreeNode segTree[n+1],segTree[1]表示根节点。
那么对于节点segTree[i],它的左孩子是segTree[2*i],右孩子是segTree[2*i+1]。
我们可以从根节点开始,平分区间,递归的创建线段树,线段树的创建函数如下:
主要思想是递归构造,如果当前节点记录的区间只有一个值,则直接赋值,否则递归构造左右子树,最后回溯的时候给当前节点赋值。
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 1005;
struct SegTreeNode{
int val;
};
SegTreeNode segTree[maxn];
/*
功能:构建线段树
root:当前线段树的根节点下标
arr: 用来构造线段树的数组
istart:数组的起始位置
iend:数组的结束位置
*/
void build(int root,int arr[],int istart,int iend)
{
if(istart == iend) //叶子结点
segTree[root].val = arr[istart]; /* 只有一个元素,节点记录该单元素 */
else{
int mid = (istart + iend)/2;
build(2*root,arr,istart,mid); //递归构造左子树
build(2*root+1,arr,mid+1,iend); //递归构造右子树
//根据左右子树根节点的值,更新当前根节点的值
segTree[root].val = min(segTree[2*root].val,segTree[2*root+1].val); /* 回溯时得到当前node节点的线段信息 */
}
}
int main()
{
int array[maxn];
array[0] = 1, array[1] = 2,array[2] = 2, array[3] = 4, array[4] = 1, array[5] = 3;
build(1,array,0,5);
for(int i = 1; i<=20; ++i)
cout<< "seg"<< i << "=" <<segTree[i].val<<endl;
return 0;
}
此build构造成的树如图:


- 查询线段树
已经构建好了线段树,那么怎样在它上面查找某个区间的最小值呢?
查询的思想是选出一些区间,使他们相连后恰好涵盖整个查询区间,因此线段树适合解决“相邻的区间的信息可以被合并成两个区间的并区间的信息”的问题。
主要思想是把所要查询的区间[a,b]划分为线段树上的节点,然后将这些节点代表的区间合并起来得到所需信息。
比如前面一个图中所示的树,如果询问区间是[0,2],或者询问的区间是[3,3],不难直接找到对应的节点回答这一问题。
代码如下,具体见代码解释
/*
功能:线段树的区间查询
root:当前线段树的根节点下标,也称当前查询节点
[nstart, nend]: 当前节点所表示的区间,也称当前节点存储的区间
[qstart, qend]: 此次查询的区间
*/
int query(int root, int nstart, int nend, int qstart, int qend)
{
//查询区间和当前节点区间没有交集
if(qstart > nend || qend < nstart)
return INF;
//当前节点区间包含在查询区间内
if(qstart <= nstart && qend >= nend)
return segTree[root].val;
//分别从左右子树查询,返回两者查询结果的较小值
int mid = (nstart + nend) / 2;
return min(query(root*2, nstart, mid, qstart, qend),
query(root*2+1, mid + 1, nend, qstart, qend));
}
可见,这样的过程一定选出了尽量少的区间,它们相连后正好涵盖了整个[qstart,qend],没有重复也没有遗漏。同时,考虑到线段树上每层的节点最多会被选取2个,一共选取的节点数也是O(logn)的,因此查询的时间复杂度也是O(logn)。
线段树并不适合所有区间查询情况,它的使用条件是“相邻的区间的信息可以被合并成两个区间的并区间的信息”。即问题是可以被分解解决的。
举例说明(对照上面的二叉树):
1、当我们要查询区间[0,2]的最小值时,从根节点开始,要分别查询左右子树,查询左子树时节点区间[0,2]包含在查询区间[0,2]内,返回当前节点的值1,查询右子树时,节点区间[3,5]和查询区间[0,2]没有交集,返回正无穷INF,查询结果取两子树查询结果的较小值1,因此结果是1。
2、查询区间[0,3]时,从根节点开始,查询左子树的节点区间[0,2]包含在区间[0,3]内,返回当前节点的值1;查询右子树时,继续递归查询右子树的左右子树,查询到非叶节点4时,又要继续递归查询:叶子节点4的节点区间[3,3]包含在查询区间[0,3]内,返回4,叶子节点9的节点区间[4,4]和[0,3]没有交集,返回INF,因此非叶节点4返回的是min(4, INF) = 4,叶子节点3的节点区间[5,5]和[0,3]没有交集,返回INF,因此非叶节点3返回min(4, INF) = 4,因此根节点返回 min(1,4) = 1。
- 单节点更新
单节点更新是指只更新线段树的某个叶子节点的值,但是更新叶子节点会对其父节点的值产生影响,因此更新子节点后,要回溯更新其父节点的值。
/*
功能:更新线段树中某个叶子节点的值
root:当前线段树的根节点下标
[nstart, nend]: 当前节点所表示的区间
index: 待更新节点在原始数组arr中的下标
addVal: 更新的值(原来的值加上addVal)
*/
void updateOne(int root, int nstart, int nend, int index, int addVal)
{
if(nstart == nend)
{
if(index == nstart)//找到了相应的节点,更新之
segTree[root].val += addVal;
return;
}
int mid = (nstart + nend) / 2;
if(index <= mid)//在左子树中更新
updateOne(root*2, nstart, mid, index, addVal);
else updateOne(root*2+1, mid+1, nend, index, addVal);//在右子树中更新
//根据左右子树的值回溯更新当前节点的值
segTree[root].val = min(segTree[root*2].val, segTree[root*2+1].val);
}
比如我们要更新叶子节点4(addVal = 6),更新后值变为10,那么其父节点的值从4变为9,非叶结点3的值更新后不变,根节点更新后也不变。
- 区间更新(线段树中最有用的)
区间更新是指更新某个区间内的叶子节点的值,因为涉及到的叶子节点不止一个,而叶子节点会影响其相应的非叶父节点,那么回溯需要更新的非叶子节点也会有很多,如果一次性更新完,操作的时间复杂度肯定不是O(logn),例如当我们要更新区间[0,3]内的叶子节点时,需要更新除了叶子节点3,9外的所有其他节点。为此引入了线段树中的延迟标记概念,这也是线段树的精华所在。
延迟标记:每个节点新增加一个标记域,记录这个节点是否进行了某种修改(这种修改操作会影响其子节点),对于任意区间的修改,我们先按照区间查询的方式将其划分成线段树中的节点,然后修改这些节点的信息,并给这些节点标记上代表这种修改操作的标记。在修改和查询的时候,如果我们到了一个节点p,并且决定考虑其子节点,那么我们就要看节点p是否被标记,如果有,就要按照标记修改其子节点的信息,并且给子节点都标上相同的标记,同时消掉节点p的标记。(优点在于,不用将区间内的所有值都暴力更新,大大提高效率,因此区间更新是最优用的操作)
因此需要在线段树结构中加入延迟标记域,本文例子中我们加入标记域addMark,表示节点的子孙节点在原来的值的基础上加上addMark的值,同时还需要修改创建函数build 和 查询函数 query,其中区间更新的函数为update,代码如下:
const int INF = INT_MAX;
const int maxn = 1000;
struct SegTreeNode
{
int val;
int addMark; //延迟标记,节点中的标记域可以解决N多种问题
}segTree[maxn]; //定义线段树
/*
功能:构建线段树
root:当前线段树的根节点下标
arr: 用来构造线段树的数组
istart:数组的起始位置
iend:数组的结束位置
*/
void build(int root, int arr[], int istart, int iend)
{
segTree[root].addMark = 0; //----设置标延迟记域
if(istart == iend)//叶子节点
segTree[root].val = arr[istart];
else
{
int mid = (istart + iend) / 2;
build(root*2, arr, istart, mid);//递归构造左子树
build(root*2+1, arr, mid+1, iend);//递归构造右子树
//根据左右子树根节点的值,更新当前根节点的值
segTree[root].val = min(segTree[root*2].val, segTree[root*2+1].val);
}
}
/*
功能:当前节点的标志域向孩子节点传递
root: 当前线段树的根节点下标
*/
void pushDown(int root)
{
if(segTree[root].addMark != 0)
{
//设置左右孩子节点的标志域,因为孩子节点可能被多次延迟标记又没有向下传递
//所以是 “+=”
segTree[root*2].addMark += segTree[root].addMark;
segTree[root*2+1].addMark += segTree[root].addMark;
//根据标志域设置孩子节点的值。因为我们是求区间最小值,因此当区间内每个元
//素加上一个值时,区间的最小值也加上这个值
segTree[root*2].val += segTree[root].addMark;
segTree[root*2+1].val += segTree[root].addMark;
//传递后,当前节点标记域清空
segTree[root].addMark = 0;
}
}
/*
功能:线段树的区间查询
root:当前线段树的根节点下标
[nstart, nend]: 当前节点所表示的区间
[qstart, qend]: 此次查询的区间
*/
int query(int root, int nstart, int nend, int qstart, int qend)
{
//查询区间和当前节点区间没有交集
if(qstart > nend || qend < nstart)
return INF;
//当前节点区间包含在查询区间内
if(qstart <= nstart && qend >= nend)
return segTree[root].val;
//分别从左右子树查询,返回两者查询结果的较小值
pushDown(root); //----延迟标志域向下传递
int mid = (nstart + nend) / 2;
return min(query(root*2, nstart, mid, qstart, qend),
query(root*2+1, mid + 1, nend, qstart, qend));
}
/*
功能:更新线段树中某个区间内叶子节点的值
root:当前线段树的根节点下标
[nstart, nend]: 当前节点所表示的区间
[ustart, uend]: 待更新的区间
addVal: 更新的值(原来的值加上addVal)
*/
void update(int root, int nstart, int nend, int ustart, int uend, int addVal)
{
//更新区间和当前节点区间没有交集
if(ustart > nend || uend < nstart)
return ;
//当前节点区间包含在更新区间内
if(ustart <= nstart && uend >= nend)
{
segTree[root].addMark += addVal;
segTree[root].val += addVal;
return ;
}
pushDown(root); //延迟标记向下传递
//更新左右孩子节点
int mid = (nstart + nend) / 2;
update(root*2, nstart, mid, ustart, uend, addVal);
update(root*2+1, mid+1, nend, ustart, uend, addVal);
//根据左右子树的值回溯更新当前节点的值
segTree[root].val = min(segTree[root*2].val, segTree[root*2+1].val);
}
区间更新举例说明:当我们要对区间[0,2]的叶子节点增加2,利用区间查询的方法从根节点开始找到了非叶子节点[0-2],把它的值设置为1+2 = 3,并且把它的延迟标记设置为2,更新完毕;当我们要查询区间[0,1]内的最小值时,查找到区间[0,2]时,发现它的标记不为0,并且还要向下搜索,因此要把标记向下传递,把节点[0-1]的值设置为2+2 = 4,标记设置为2,节点[2-2]的值设置为1+2 = 3,标记设置为2(其实叶子节点的标志是不起作用的,这里是为了操作的一致性),然后返回查询结果:[0-1]节点的值4;当我们再次更新区间[0,1](增加3)时,查询到节点[0-1],发现它的标记值为2,因此把它的标记值设置为2+3 = 5,节点的值设置为4+3 = 7;
其实当区间更新的区间左右值相等时([i,i]),就相当于单节点更新,单节点更新只是区间更新的特例。
三、经典模板
- 求区间的最值
- 连续区间的动态查询问题
- 区间求和
模板1:
RMQ,查询区间最值下标---min
#include<iostream>
using namespace std;
#define MAXN 100
#define MAXIND 256 //线段树节点个数
//构建线段树,目的:得到M数组.
void build(int node, int b, int e, int M[], int A[])
{
if (b == e)
M[node] = b; //只有一个元素,只有一个下标
else
{
build(2 * node, b, (b + e) / 2, M, A);
build(2 * node + 1, (b + e) / 2 + 1, e, M, A);
if (A[M[2 * node]] <= A[M[2 * node + 1]])
M[node] = M[2 * node];
else
M[node] = M[2 * node + 1];
}
}
//找出区间 [i, j] 上的最小值的索引
int query(int node, int b, int e, int M[], int A[], int i, int j)
{
int p1, p2;
//查询区间和要求的区间没有交集
if (i > e || j < b)
return -1;
if (b >= i && e <= j)
return M[node];
p1 = query(2 * node, b, (b + e) / 2, M, A, i, j);
p2 = query(2 * node + 1, (b + e) / 2 + 1, e, M, A, i, j);
//return the position where the overall
//minimum is
if (p1 == -1)
return M[node] = p2;
if (p2 == -1)
return M[node] = p1;
if (A[p1] <= A[p2])
return M[node] = p1;
return M[node] = p2;
}
int main()
{
int M[MAXIND]; //下标1起才有意义,否则不是二叉树,保存下标编号节点对应区间最小值的下标.
memset(M,-1,sizeof(M));
int a[]={3,4,5,7,2,1,0,3,4,5};
build(1, 0, sizeof(a)/sizeof(a[0])-1, M, a);
cout<<query(1, 0, sizeof(a)/sizeof(a[0])-1, M, a, 0, 5)<<endl;
return 0;
}
模板2:
连续区间修改或者单节点更新的动态查询问题 (此模板查询区间和)
#include <cstdio>
#include <algorithm>
using namespace std;
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
#define root 1 , N , 1
#define LL long long
const int maxn = 111111;
LL add[maxn<<2];
LL sum[maxn<<2];
void PushUp(int rt) {
sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void PushDown(int rt,int m) {
if (add[rt]) {
add[rt<<1] += add[rt];
add[rt<<1|1] += add[rt];
sum[rt<<1] += add[rt] * (m - (m >> 1));
sum[rt<<1|1] += add[rt] * (m >> 1);
add[rt] = 0;
}
}
void build(int l,int r,int rt) {
add[rt] = 0;
if (l == r) {
scanf("%lld",&sum[rt]);
return ;
}
int m = (l + r) >> 1;
build(lson);
build(rson);
PushUp(rt);
}
void update(int L,int R,int c,int l,int r,int rt) {
if (L <= l && r <= R) {
add[rt] += c;
sum[rt] += (LL)c * (r - l + 1);
return ;
}
PushDown(rt , r - l + 1);
int m = (l + r) >> 1;
if (L <= m) update(L , R , c , lson);
if (m < R) update(L , R , c , rson);
PushUp(rt);
}
LL query(int L,int R,int l,int r,int rt) {
if (L <= l && r <= R) {
return sum[rt];
}
PushDown(rt , r - l + 1);
int m = (l + r) >> 1;
LL ret = 0;
if (L <= m) ret += query(L , R , lson);
if (m < R) ret += query(L , R , rson);
return ret;
}
int main() {
int N , Q;
scanf("%d%d",&N,&Q);
build(root);
while (Q --) {
char op[2];
int a , b , c;
scanf("%s",op);
if (op[0] == 'Q') {
scanf("%d%d",&a,&b);
printf("%lld\n",query(a , b ,root));
} else {
scanf("%d%d%d",&a,&b,&c);
update(a , b , c , root);
}
}
return 0;
}
模板3:
多维空间的动态查询
四、沙场练兵
在代码前先介绍一些我的线段树风格:
- maxn是题目给的最大区间,而节点数要开4倍,确切的来说节点数要开大于maxn的最小2x的两倍
- lson和rson分辨表示结点的左儿子和右儿子,由于每次传参数的时候都固定是这几个变量,所以可以用预定于比较方便的表示
- 以前的写法是另外开两个个数组记录每个结点所表示的区间,其实这个区间不必保存,一边算一边传下去就行,只需要写函数的时候多两个参数,结合lson和rson的预定义可以很方便
- PushUP(int rt)是把当前结点的信息更新到父结点
- PushDown(int rt)是把当前结点的信息更新给儿子结点
- rt表示当前子树的根(root),也就是当前所在的结点
线段树的题目整体上可以分成以下四个部分:
单点更新:最最基础的线段树,只更新叶子节点,然后把信息用PushUP(int r)这个函数更新上来
成段更新(通常这对初学者来说是一道坎),需要用到延迟标记(或者说懒惰标记),简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要更新or询问到的时候
区间合并
扫描线
这类题目需要将一些操作排序,然后从左到右用一根扫描线(当然是在我们脑子里)扫过去最典型的就是矩形面积并,周长并等题



