博客作业06--图
1.学习总结
1.1 图的思维导图
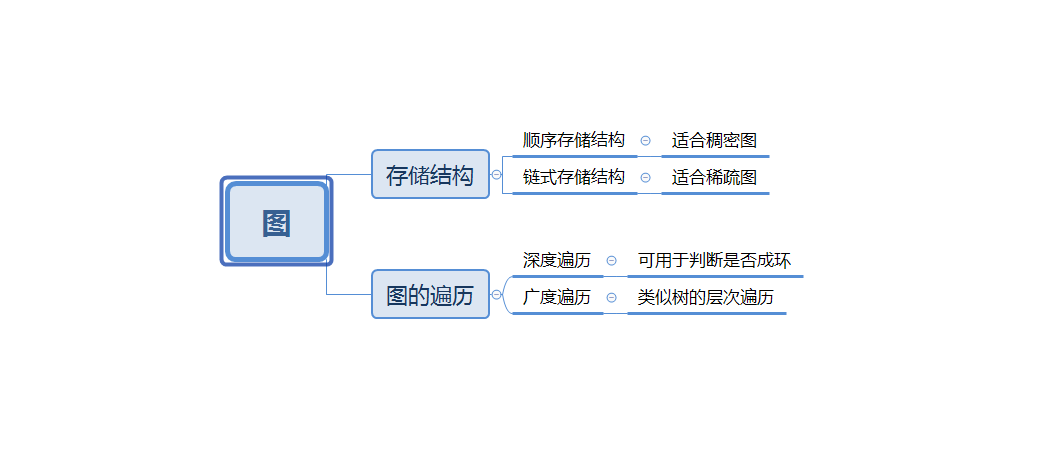
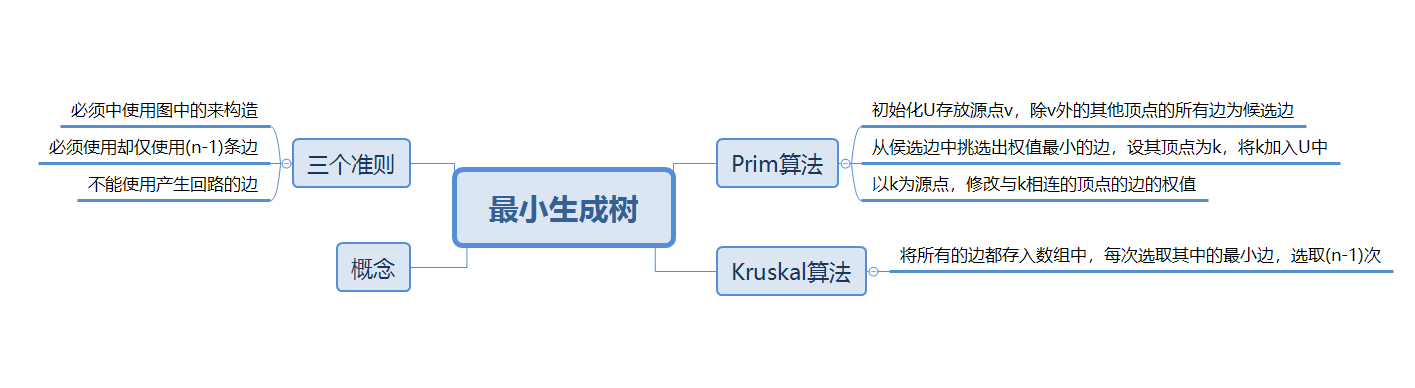
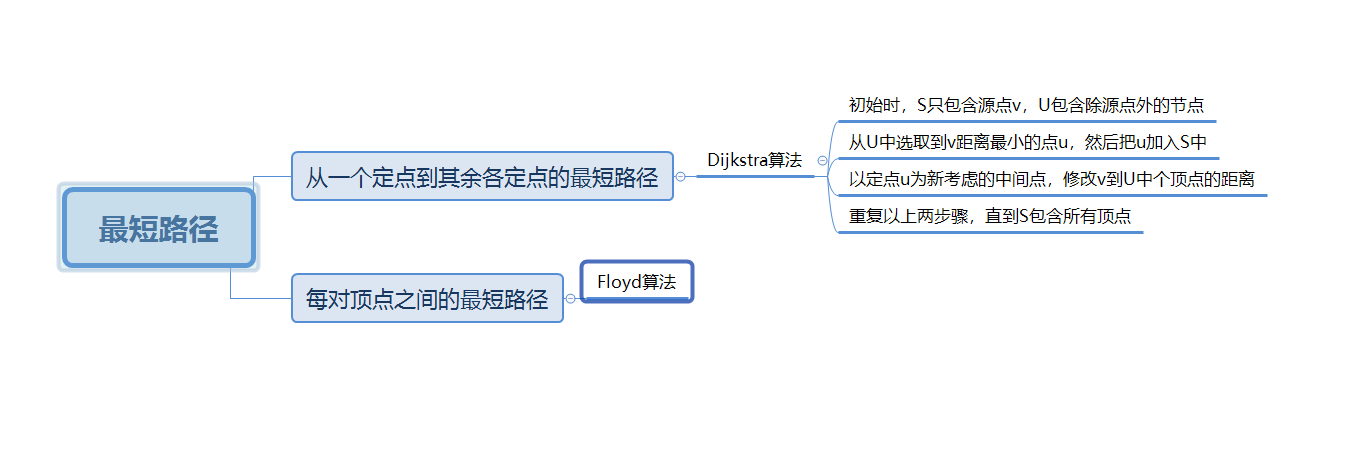

1.2图的学习体会
对于图的学习,一次看下感觉很多个算法,但是将算法分类一下就会比较容易记忆。
- 首先是对图的遍历,深度和广度遍历,深度遍历因为是用递归的方法写的,所以只要写出对其中一个节点的遍历就行(递归都是这样),而广度遍历只要类比树的层次遍历就行了。
- 其次求最小生成树,Prim和Kruscal算法,这两个算法里Kruscal算法比较好理解,就是找前(n-1)小条边,但是代码比较复杂,Prim算法理解起来也不难,每次找距离最小的,然后修改距离,代码相对较简单。
- 然后是Dijkstra算法,这个算法和Prim算法有点相似,学完Prim算法后理解起来比较容易,但是千万不要弄混了两个算法。这个算法用代码不难,但是如果是简答题把过程写出来一定要根据代码的思路来走,不然很容易找错最小值。
- 最后是拓扑排序,这个算法比较简单,代码也不难,应用了栈或队列,顶点信息中多加了一个对入度的统计count,将入度为0的顶点入栈,出栈后每个与它相连的节点的入度-1,若有入度为0的节点再入栈,直到栈空。
算法方面就是这些,对于图的学习最主要把每一步都写出来,每一步图怎变的,权值怎么改变的都要写出来,特别是后面几个算法,多找几个题目一步步写几遍,然后去看代码更容易理解。
2. PTA实验作业
题目1:公路村村通
设计思路
本题主要是找最小生成树,采用Prim算法
main(){
输入n,e;
判断n-1是否小于e,即是否能构成连通图
建立邻接矩阵
通过Prim算法获得最小长度
输出最小长度
}
Prim算法{
定义数组lowcost[MAXV],closest[MAXV];count=0,sum=0;
for i=1 to n
初始化lowcost,closest数组
end for
for i=1 to n
在lowcost数组中找出最小值min,并记下对应下标k;
end for
sum+=min;count++;lowcost[k]=0;
for i=1 to n
判断与k相连的节点的距离是否小于lowcost
是,对lowcost数组进行修改
end for
判断count==n,即图是否连通
返回sum
}
代码截图
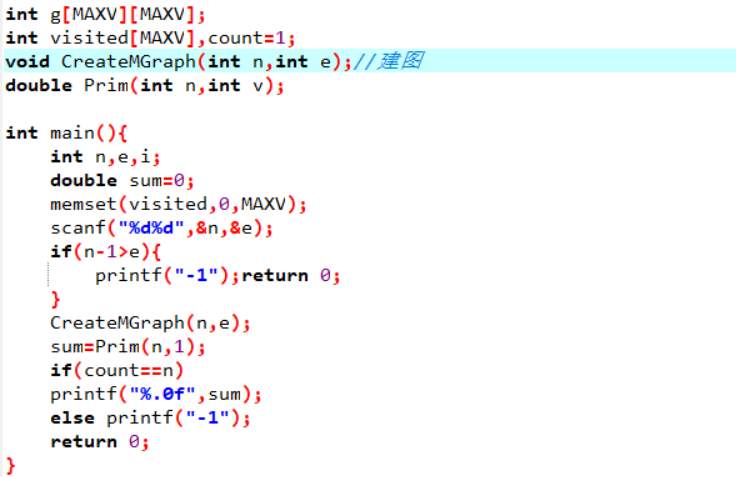


PTA提交列表说明
提交列表截图
本题碰到的主要问题为,图是否连通,最开始通过深度遍历后对visited数组进行判断,后来改成通过count进行判断,没找到一个最小值就令count++,最后通过count的值与n的值进行比较,判断图是否连通
题目2:图着色问题
设计思路
本题需先对输入的颜色的种类进行判断,是否等于给的颜色种类
main()
{
输入n,e,k;
建立邻接矩阵
输入颜色方案v;
for i=0 to v
输入颜色
舒适化visited数组
判断颜色if(Judege(color,n,k))
flag=1;
for l=0 to n
深度遍历判断方案是否正确DFS(l,n);
若遍历过程中flag==0,break
end for
根据flag输出yes/no
end if
else 输出no
end for
}
int Judege(int color[],int n,int k){
调用set头文件set<int> s
for i=0 to n
将color数组中元素都插入s,s.insert(color[i]);
end for
判断s中元素是否与k相等,若相等返回1,否则返回0
}
void DFS(int v,int n){
若该定点已经访问过或者flag=0,return
visited[v]=1;
for i=1 to n
若与v相连的节点的颜色与v相同
flag=0;return
若与v相连节点没有访问过,则递归DFS(i,n)
}
代码截图

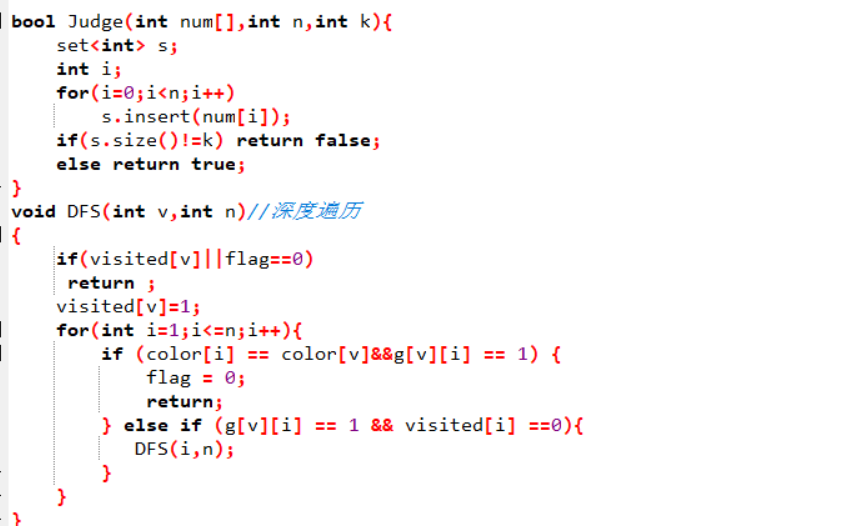

PTA提交列表说明
提交列表
本题的错误点比较多
- 一开始是没有对输入的颜色的种类进行判断,于是写了一个Judge函数对每次输入的颜色方案进行种类的判断,其中用到了set头文件,只要把颜色都插入set中,最后判断set的大小就能知道有几种颜色,最后和k进行比较。
- 图不连通。本题我用链式和顺序存储结构都试了,最后都是图不连通的时候错误,错误的原因是我只进行了一次深度遍历,每次都是从编号为1的节点开始,倒是有的时候不能判断出来,后来改成循环,让每个节点都深度遍历一次。

原来的:
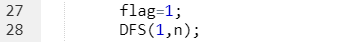
修改后:

题目3:旅游规划
设计思路
本题是对Dijkstra算法的应用
定义结构体edge{
int dist,price;
}
int dist[MAXV],price[MAXV];
main(){
输入n,m,s,d;
edge edges[MAXV][MAXV]
建立邻接矩阵CreateMGraph(edges)
Dijkstra算法计算最短路径Dijkstra(edges,s);
输出dist[d],price[d];
}
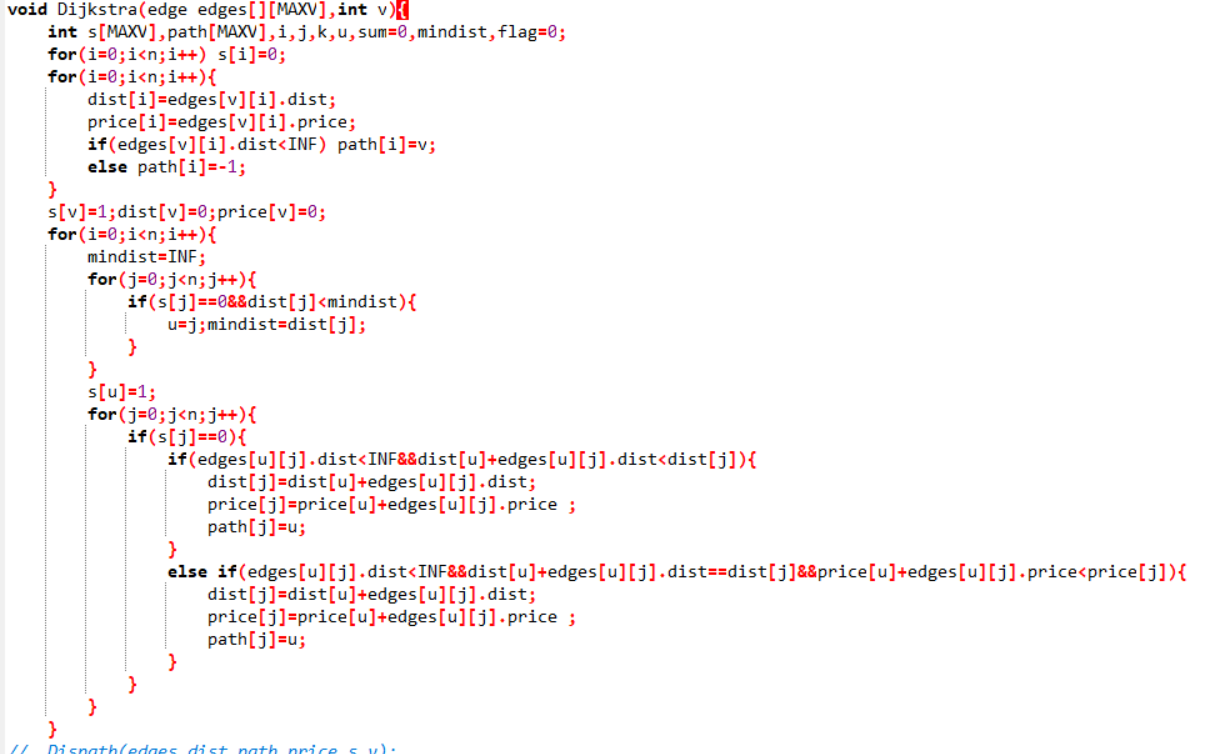
Dijkstra算法(edge edges[][MAXV],int v){
定义s[MAXV],path[MAXV],sum=0,min,i,j,k,u;
初始化s数组,memset(s,0,MAXV);
for i=0 to n
初始化dist,price数组,分别等于edges[v][i].dist,edges[v][i].price;
if edges[i][v]<INF path[i]=v
else path[i]=-1;
end for
v加入s数组
for i=0 to n
min=INF;
for j=0 to n
在dist数组中找到不在s数组中的节点的最小值,并记下下标u
end for
将u加入s数组
for j=0 to n
若u到j的距离加上v到u的距离比v到j的距离更短 ,修改price,dist,path数组
若u到j的距离加上v到u的距离与v到j的距离相等但u到j的花费加上v到u的花费比v到j的花费更小,修改price,dist,path数组
end for
}
代码截图


PTA提交列表说明

本题没碰到什么问题
3.截图本周题目集的PTA最后排名
PTA排名

我的总分
我的总分:2.5分
4.阅读代码
题目:欧拉回路
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。
能否走过这样的七座桥,并且每桥只走一次?瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡七桥问题,并证明了更为广泛的有关一笔画的三条结论,人们通常称之为欧拉定理。对于一个连通图,通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。
你的任务是:对于给定的一组无向图数据,判断其是否成其为欧拉图
代码
#include<iostream>
#include<string.h>
using namespace std;
int mp[1010][1010];
int vis[1010];
int d[1010];//记录入度出度
int n,m,sum;
void DFS(int t)
{
vis[t]=1;
sum++;//记录遍历时所经过的点的数目
for(int i=1;i<=n;i++)
{
if(!vis[i]&&mp[t][i])
{
DFS(i);
}
}
}
int main()
{
int T,u,v;
cin>>T;
while(T--)
{
cin>>n>>m;
memset(vis,0,sizeof(vis));
memset(mp,0,sizeof(mp));
memset(d,0,sizeof(d));
while(m--)
{
cin>>u>>v;
mp[u][v]=mp[v][u]=1;
d[u]++;
d[v]++;
}
sum=0;//注意sum为全局变量
//int sum=0;即为错误,局部变量覆盖全局变量,sum只会为0
DFS(u);
int k=1;
for(int i=1;i<=n;i++)
{
if(d[i]%2!=0)//
{
k=0;
break;
}
}
if(k&&sum==n)//入度都为偶数且为连通图;
cout<<1<<endl;
else
cout<<0<<endl;
}
return 0;
}
注:欧拉回路
<无向图>
定理1:无向图G是欧拉图当且仅当G是连通图,且G中没有奇度顶点。
定理2:无向图G是半欧拉图当且仅当G是连通图,且G中恰有两个奇度顶点。
<有向图>
定理1:有向图D是欧拉图当且仅当D是强连通的且每个顶点的入度都等于出度。
定理2:有向图D是半欧拉图当且仅当D是单向连通的,且D中恰有两个奇度顶点,其
中一个入度比出度大1,另一个的出度比入度大1,而其余顶点的入度都等于
出度。


