图-马晓萱
1.学习总结(2分)
1.1图的思维导图
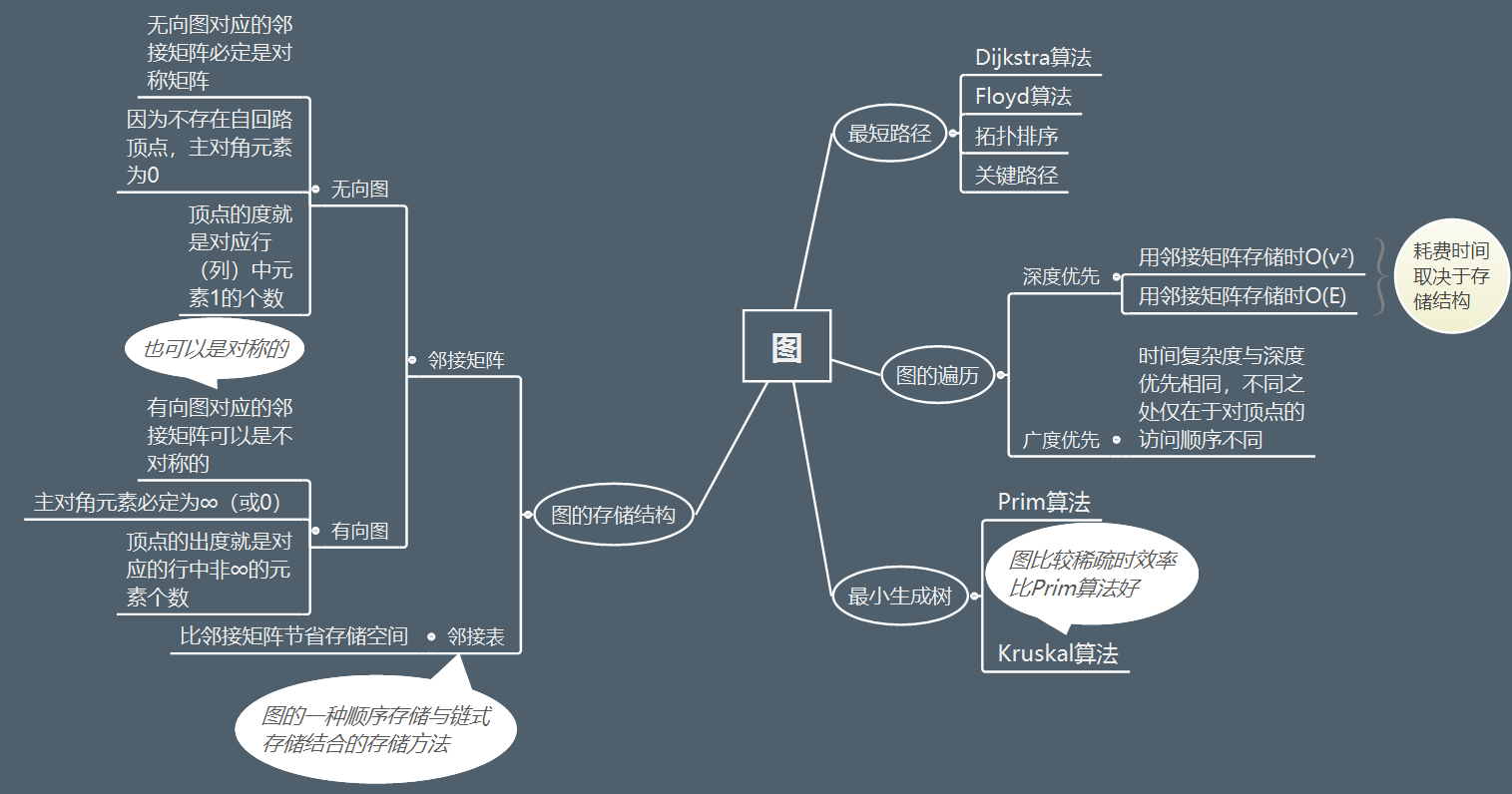
1.2 图结构学习体会
- 深度遍历算法 :访问到已被访问过的邻接点时要递归回退到上一个邻接点,直到出现没有访问过的邻接点
- 广度遍历算法:类似于树的层次遍历
- Prim和Kruscal算法:Prim算法,每次都选择权值最小的边,如果加入一条边会让图有回路就要返回到上一个邻接点,直到选择一条不出现回路的为止
Kruscal算法 ,把孤立顶点合成森林的过程 - Dijkstra算法:类似于Prim算法,但不断的更新
- 拓扑排序算法:每次找到入度为0的顶点输出,并删除这个顶点与它相连的所有边,直到所有顶点输出。
2.1 题目1:7-2 排座位
2.2 设计思路
定义一个二维数组存储两两之间的关系,1为朋友,-1为敌对。
2.3 代码截图
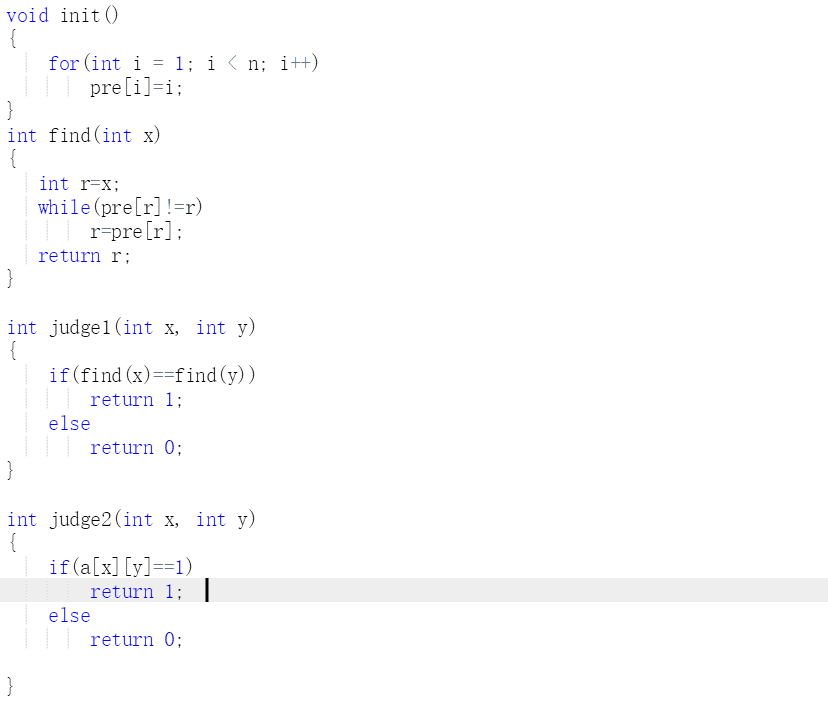
2.4 PTA提交列表说明
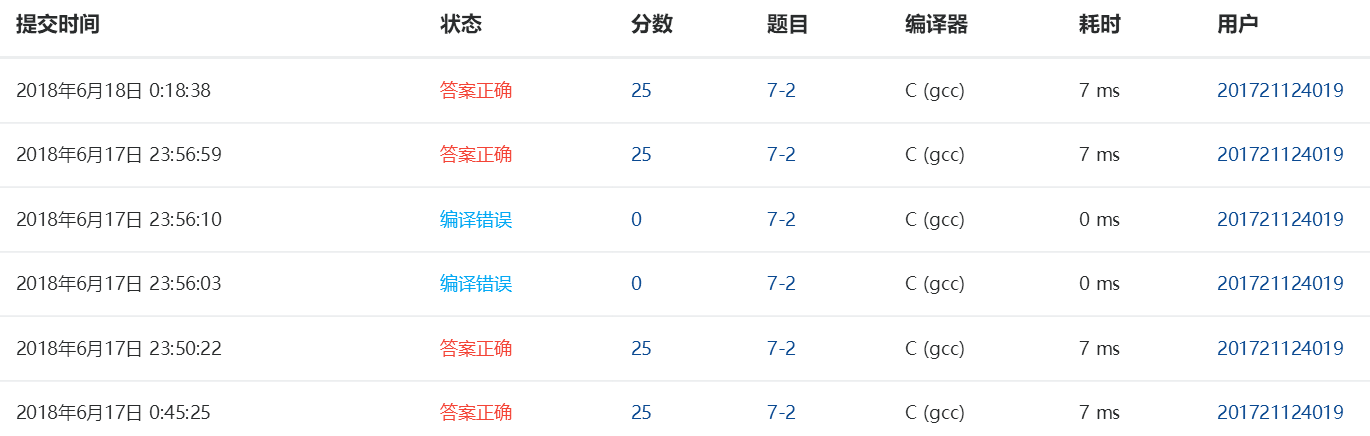
题目2:7-5 畅通工程之最低成本建设问题
2.2 设计思路
就是求图的最小生成树
2.3 代码截图
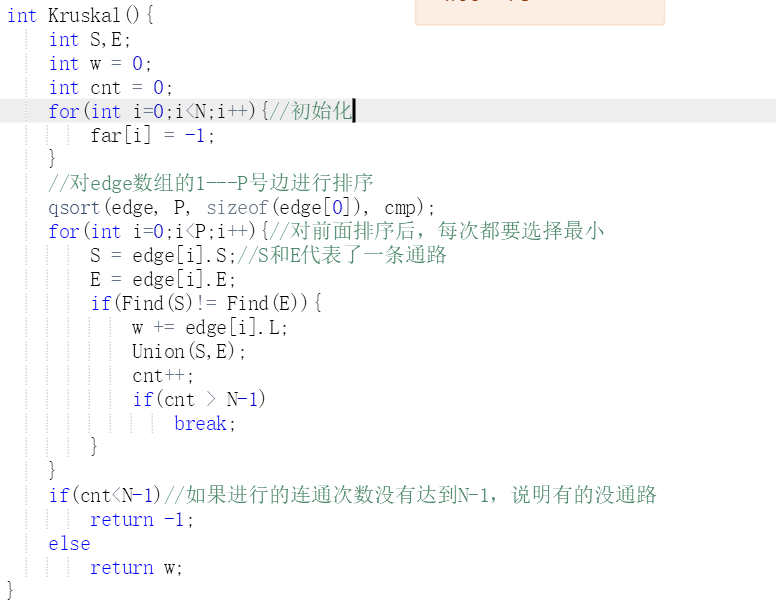
2.4 PTA提交列表说明
题目3:7-4 公路村村通
2.2 设计思路
最小生成树与最短路径之间的区别很容易想到用最小生成树,本来想floyd算法求出最短路径然后相加了,但是不能保证成本是最低的。 这里用了Prim算法
2.3 代码截图

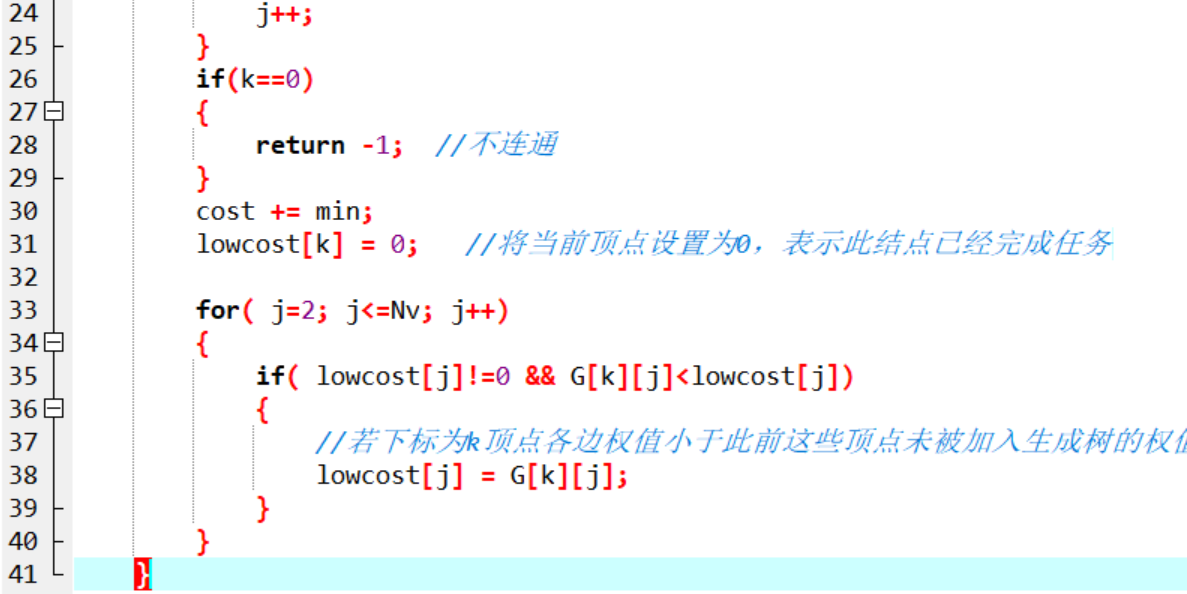
2.4 PTA提交列表说明

3.截图本周题目集的PTA最后排名
4. 阅读代码(必做,1分)
#include<stdio.h>
#include<stdlib.h>
#define MAXVEX 105
#define INFINITY 65535
void CreateGraph( );
void Floyd();
void FindAnimal();
int FindMax( int i);
int G[MAXVEX][MAXVEX],Nv,Ne;
int D[MAXVEX][MAXVEX]; //存储最短路径矩阵
int main()
{
CreateGraph();
FindAnimal();
return 0;
}
void CreateGraph()
{
//用邻接矩阵表示图
int i,j;
int v1,v2,w;
scanf("%d %d",&Nv,&Ne);
for( i=1; i<=Nv; i++)
{
for( j=1; j<=Nv; j++)
{
if( i==j){
G[i][j] = 0;
}
else G[i][j] = INFINITY; //初始化
}
}
for( i=0; i<Ne; i++) //这里是读入边
{
scanf("%d %d %d",&v1,&v2,&w);
G[v1][v2] = w; //读入权值
G[v2][v1]= G[v1][v2]; //无向图对称
}
}
void FindAnimal()
{
int max,min;
int animal;
int i;
Floyd();
min = INFINITY;
for( i=1; i<=Nv; i++)
{
//比较每行最大距离,寻找其中最小值
max = FindMax( i );
if( max == INFINITY)
{
//判断图是否连同通
printf("0\n");
return;
}
if( min>max )
{
min = max;
animal = i;
}
}
printf("%d %d\n",animal,min);
}
int FindMax( int i)
{
int max;
int j;
max = 0;
for( j=1; j<=Nv; j++)
{
if( i!=j && D[i][j]>max)
{
max = D[i][j];
}
}
return max;
}
void Floyd()
{
int i,j,k;
for( i=1; i<=Nv; i++)
{
for( j=1; j<=Nv; j++)
{
D[i][j] = G[i][j];
}
}
//注意动物是从下标1开始编号
for ( k=1; k<=Nv; k++)
{
for( i=1; i<=Nv; i++)
{
for( j=1; j<=Nv; j++)
{
if( D[i][k]+D[k][j] < D[i][j])
{
D[i][j] = D[i][k]+D[k][j];
}
}
}
}
}
图的最短路径Floyd算法




