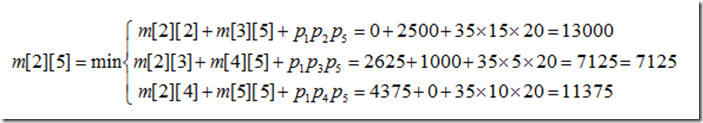矩阵连乘问题
题目描述
给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2…,n-1。如何确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。
题目分析
算法实现
/*
* 矩阵连乘积A1A2A3A4A5A6最优计算次序
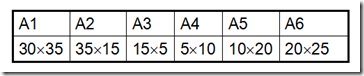
* A1: 30 x 35
* A2: 35 x 15
* A3: 15 x 5
* A4: 5 x 10
* A5: 10 x 20
* A6: 20 x 25
*
* 最优计算次序:((A1(A2A3))((A4A5)A6))
* 程序输出
* Multiply A2,2 and A3,3
* Multiply A1,1 and A2,3
* Multiply A4,4 and A5,5
* Multiply A4,5 and A6,6
* Multiply A1,3 and A4,6
*/
#include <iostream>
using namespace std;
/*
* 计算最优值
* 输出:最优值数组m,记录最优断开位置的数组s
*/
void matrixChain(int *p, int n, int m[][7], int s[][7])
{
for (int i = 1; i <= n; i++)
{
m[i][i] = 0;
}
for (int r = 2; r <= n; r++)
{
for (int i = 1; i <= n - r + 1; i++)
{
int j = i + r - 1;
m[i][j] = m[i][i] + m[i + 1][j] + p[i - 1] * p[i] * p[j];
s[i][j] = i;
for (int k = i + 1; k < j; k++)
{
int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (t < m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
/* 构造最优解 */
void traceback(int i, int j, int s[][7])
{
if (i == j)
{
return;
}
traceback(i, s[i][j], s);
traceback(s[i][j] + 1, j, s);
cout << "Multiply A" << i << "," << s[i][j];
cout << " and A" << (s[i][j] + 1) << "," << j << endl;
}
int main()
{
int p[7] = { 30, 35, 15, 5, 10, 20, 25 };
int m[7][7] = { 0 };
int s[7][7] = { 0 };
matrixChain(p, 6, m, s);
traceback(1, 6, s);
getchar();
return 0;
}
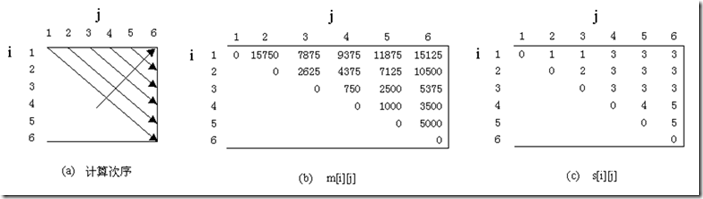
动态规划算法matrixChain计算m[i][j]先后次序如图(a)所示;计算结果m[i][j]和s[i][j],1<= i <= j <=n,分别如图(b)和(c)所示。
例如,在计算m[2][5]时,依递归式有
且k=3,因此,s[2][5]=3。
复杂性分析
算法matrixChain的主要计算量取决于算法中对r,i 和 k 的3重循环。循环体内的计算量为O(1),而3重循环的总次数为O(n3)。因此算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。