tensorflow(3):神经网络优化(ema,regularization)

1.指数滑动平均 (ema)

描述滑动平均:

 with tf.control_dependencies([train_step,ema_op]) 将计算滑动平均与 训练过程绑在一起运行

    train_op=tf.no_op(name='train')  使它们合成一个训练节点

#定义变量一级滑动平均类
#定义一个32位浮点变量,初始值为0.0, 这个代码就是在不断更新w1参数,优化 w1,滑动平均做了一个w1的影子
w1=tf.Variable(0,dtype=tf.float32)
#定义num_updates(NN 的迭代次数)初始值为0, global_step不可被优化(训练) 这个额参数不训练
global_step=tf.Variable(0,trainable=False)
#设置衰减率0.99 当前轮数global_step
MOVING_AVERAGE_DECAY=0.99
ema=tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY,global_step)
#ema.apply后面的括号是更新列表,每次运行sess.run(ema_op)时,对更新列表中的元素求滑动平均值,
#在实际应用中会使用tf.trainable_variable()自动将所有待训练的参数汇总为列表
#ema_op=ema.apply([w1])
ema_op=ema.apply(tf.trainable_variables())

#查看不同迭代中变量的取值变化
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    #ema_op=ema.apply([w1])获取w1 的滑动平均值,
    print(sess.run([w1,ema.average(w1)])) #打印当前参数w1和w1 的滑动平均值 (0,0)
    sess.run(tf.assign(w1,1))
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)])) #(1,0.9)
    #跟新step w1的值,模拟出100轮迭代后,参数w1 变为10
    sess.run(tf.assign(global_step,100))
    sess.run(tf.assign(w1,10))
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)])) #(10,1.644)
    
    #每次sess.run会更新一次w1的滑动平均值
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)]))
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)]))
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)]))
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)]))
    sess.run(ema_op)
    print(sess.run([w1,ema.average(w1)]))

结果:

 [0.0, 0.0]
[1.0, 0.9]
[10.0, 1.6445453]
[10.0, 2.3281732]
[10.0, 2.955868]
[10.0, 3.532206]
[10.0, 4.061389]
[10.0, 4.547275]

w1的移动平均会越来越趋近于w1 ...

 

2.正则化regularization

有时候模型对训练集的正确率很高, 却对新数据很难做出正确的相应, 这个叫过拟合现象.

加入噪声后,loss变成了两个部分,前者是以前讲过的普通loss,

后者的loss(w)有两种求法,分别称为L1正则化与 L2正则化

以下举例说明:

 代码:

atch_size=30
#建立数据集
seed=2
rdm=np.random.RandomState(seed)
X=rdm.randn(300,2)
Y_=[int(x0*x0+x1*x1<2) for (x0,x1) in X]
Y_c=[['red' if y else 'blue'] for y in Y_] #1则红色,0则蓝色
X=np.vstack(X).reshape(-1,2) #整理为n行2列,按行的顺序来
Y_=np.vstack(Y_).reshape(-1,1)# 整理为n行1列
#print(X)
#print(Y_)
#print(Y_c)
plt.scatter(X[:,0],X[:,1],c=np.squeeze(Y_c))#np.squeeze(Y_c)变成一个list
plt.show()
#print(np.squeeze(Y_c))

#定义神经网络的输入 输出 参数, 定义前向传播过程
def get_weight(shape,regularizer): #w的shape 和w的权重
    w=tf.Variable(tf.random_normal(shape),dtype=tf.float32)
    tf.add_to_collection('losses',tf.contrib.layers.l2_regularizer(regularizer)(w))
    return w

def get_bias(shape): #b的长度
    b=tf.Variable(tf.constant(0.01,shape=shape))
    return b
#
x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))
w1=get_weight([2,11],0.01)
b1=get_bias([11])
y1=tf.nn.relu(tf.matmul(x,w1)+b1) #relu 激活函数

w2=get_weight([11,1],0.01)
b2=get_bias([1])
y=tf.matmul(y1,w2)+b2  #输出层不过激活函数

#定义损失函数loss
loss_mse=tf.reduce_mean(tf.square(y-y_))
loss_total=loss_mse+tf.add_n(tf.get_collection('losses'))

#定义反向传播方法, 不含正则化, 要是使用正则化,则 为loss_total
train_step=tf.train.AdamOptimizer(0.0001).minimize(loss_mse)
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    steps=40000
    for i in range(steps):
        start=(i*batch_size)%300
        end=start+batch_size
        sess.run(train_step,feed_dict={x:X[start:end],y_:Y_[start:end]})
        if i%10000==0:
            loss_mse_v=sess.run(loss_mse,feed_dict={x:X,y_:Y_})
            print('after %d steps,loss is:%f'%(i,loss_mse_v))
    xx,yy=np.mgrid[-3:3:0.01,-3:3:0.01]
    grid=np.c_[xx.ravel(),yy.ravel()]
    probs=sess.run(y,feed_dict={x:grid})
    probs=probs.reshape(xx.shape) #调整成xx的样子
    print('w1:\n',sess.run(w1))
    print('b1:\n',sess.run(b1))
    print('w2:\n',sess.run(w2))
    print('b2:\n',sess.run(b2))
plt.scatter(X[:,0],X[:,1],c=np.squeeze(Y_c))
plt.contour(xx,yy,probs,levels=[.5]) #给probs=0.5的值上色 (显示分界线)
plt.show()

#使用个正则化
train_step=tf.train.AdamOptimizer(0.0001).minimize(loss_total)
with tf.Session() as sess:
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    steps=40000
    for i in range(steps):
        start=(i*batch_size)%300
        end=start+batch_size
        sess.run(train_step,feed_dict={x:X[start:end],y_:Y_[start:end]})
        if i%10000==0:
            loss_v=sess.run(loss_total,feed_dict={x:X,y_:Y_})
            print('after %d steps,loss is:%f'%(i,loss_v))
    xx,yy=np.mgrid[-3:3:0.01,-3:3:0.01]
    grid=np.c_[xx.ravel(),yy.ravel()]
    probs=sess.run(y,feed_dict={x:grid})
    probs=probs.reshape(xx.shape) #调整成xx的样子
    print('w1:\n',sess.run(w1))
    print('b1:\n',sess.run(b1))
    print('w2:\n',sess.run(w2))
    print('b2:\n',sess.run(b2))
plt.scatter(X[:,0],X[:,1],c=np.squeeze(Y_c))
plt.contour(xx,yy,probs,levels=[.5]) #给probs=0.5的值上色
plt.show()

结果显示:

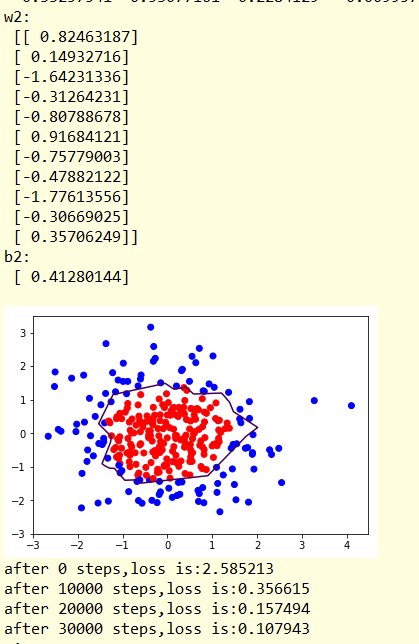
显然 经过正则化,分割线更加平滑,数据集中的噪声对模型的影响更小,