砝码称重问题求解:动态规划与母函数方法

　　砝码称重问题:设有1g、2g、3g、5g、10g、20g的砝码各若干枚（其质量<=1000g），求出用他们能称出的质量的种类数(不包括质量为0的情况)。

　　一、动态规划方法求解

　　设dp[1000]数组为标记数组。当dp[i]=0时，表示质量为i的情况，目前没有称出；当dp[i]=1时，表示质量为i的情况已经称出。

　　本题目中有多个砝码，我们顺序处理每一个砝码。

　　当处理第j个砝码，质量为wj时，有下列推导公式：

　　　　　　　　　　　　　　　　

　　完整程序代码如下：

#include<stdio.h>
#include<string.h>
int sum;  ///表示输入的砝码的总质量
int ma[6];  ///六种砝码的个数
int weight[6]={1,2,3,5,10,20};  ///六种砝码的重量
char dp[1001]; ///标记位

void input();   ///输入每个砝码的数量，并求出所有砝码的总质量sum
void exeDP();
void output();  ///判断标记为1的数量，并输出

int main()
{
    memset(dp,0,sizeof(dp));
    input();
    exeDP();
    output();
    return 0;
}

void input()
{
    int i;
    sum=0;
    for(i=0;i<6;i++)
    {
        scanf("%d",&ma[i]);
        sum=sum+(ma[i]*weight[i]);
    }
}

void exeDP()
{
    int i,j,z;
    dp[0]=1;
    for(i=0;i<6;i++)    ///六种砝码
    {
        for(j=0;j<ma[i];j++)    ///每种砝码的个数
        {
            for(z=sum;z>=weight[i];z--) ///判断每种质量是否可以被称出
            {
                if(dp[z-weight[i]]==1)
                    dp[z]=1;
            }
        }
    }
}

void output()
{
    int i,time=0;
    for(i=1;i<=sum;i++)
    {
        if(dp[i]==1)    ///若能被称出，则计数
            time++;
    }
    printf("%d",time);
}

　　二、母函数求解

　　设输入的质量为w的砝码n个，则可以用母函数表示为:

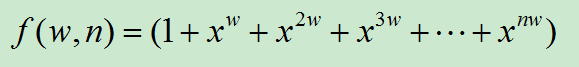
　　针对本题目，例如输入六种砝码（1g,2g,3g,5g,10g,20g）的个数分别为：1,2,2,0,0,1。则有：

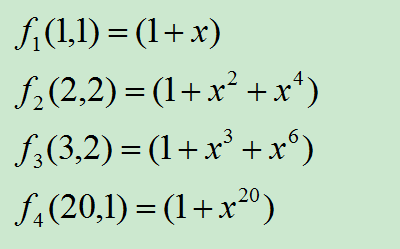
　　用matlab软件的符号计算有：

>> syms x;
>> f1=(1+x);
>> f2=(1+x^2+x^4);
>> f3=(1+x^3+x^6);
>> f4=(1+x^20);
>> expand(f1*f2*f3*f4)
>>ans=
x^31 + x^30 + x^29 + 2*x^28 + 2*x^27 + 2*x^26 + 2*x^25 + 2*x^24 + 2*x^23 + x^22 + x^21 + x^20 + x^11 + x^10 + x^9 + 2*x^8 + 2*x^7 + 2*x^6 + 2*x^5 + 2*x^4 + 2*x^3 + x^2 + x + 1

　　其中x的指数就是能够称出的质量，可知可以称出的不同质量个数为23个。