三对角矩阵(Tridiagonal Matrices)的求法：Thomas Algorithm(TDMA)

做三次样条曲线时，需要解三对角矩阵（Tridiagonal Matrices）。常用解法为Thomas Algorithm，又叫The tridiagonal matrix algorithm (TDMA)。它是一种基于高斯消元法的算法， 分为两个阶段：向前消元forward elimination和回代backward substitution。本文以一个6乘6矩阵为例，介绍一下使用TDMA的求解过程。

1.范例求解

步骤1： 将矩阵变为上三角矩阵

首先要把上面公式中的系数矩阵变为一个上三角矩阵。

第一行：

将上式除以b1：

可写作：

所以矩阵方程可写为：

第二行：

将变换后的第一行乘以a2，再与第二行相减，即可消去x1，得：

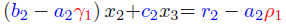
所以新的矩阵方程为：

同理可推，

第三行：

第四行：

第五行：

第六行：

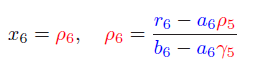
最后得到新的上三角矩阵公式为：

步骤2：求解

x逆序可以求出，如下：

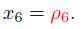
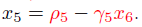
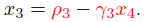
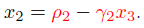
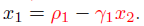
2. 一般性公式：

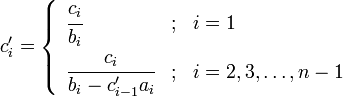
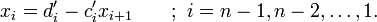
注意：

使用TDMA求解，系数矩阵需时diagonally dominant， 即：

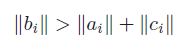
3. 实现代码（C语言）

void tdma(float x[], const size_t N, const float a[], const float b[], float c[]) 
{
        size_t n;
 
        c[0] = c[0] / b[0];
        x[0] = x[0] / b[0];

        for (n = 1; n < N; n++) {
                float m = 1.0f / (b[n] - a[n] * c[n - 1]);
                c[n] = c[n] * m;
                x[n] = (x[n] - a[n] * x[n - 1]) * m;
        }
 
        for (n = N - 1; n-- > 0; )
                x[n] = x[n] - c[n] * x[n + 1];
}