数据挖掘-决策树ID3分类算法的C++实现
转自:http://blog.csdn.net/yangliuy/article/details/7322015
作者: yangliuy
决策树算法是非常常用的分类算法,是逼近离散目标函数的方法,学习得到的函数以决策树的形式表示。其基本思路是不断选取产生信息增益最大的属性来划分样例 集和,构造决策树。信息增益定义为结点与其子结点的信息熵之差。信息熵是香农提出的,用于描述信息不纯度(不稳定性),其计算公式是
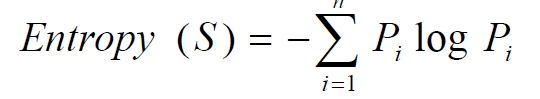
Pi为子集合中不同性(而二元分类即正样例和负样例)的样例的比例。这样信息收益可以定义为样本按照某属性划分时造成熵减少的期望,可以区分训练样本中正负样本的能力,其计算公司是

我实现该算法针对的样例集合如下
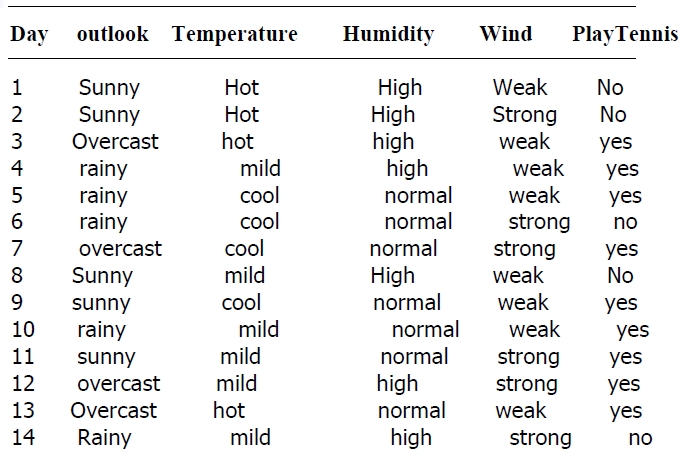
该表记录了在不同气候条件下是否去打球的情况,要求根据该表用程序输出决策树
C++代码如下,程序中有详细注释
- #include <iostream>
- #include <string>
- #include <vector>
- #include <map>
- #include <algorithm>
- #include <cmath>
- using namespace std;
- #define MAXLEN 6//输入每行的数据个数
- //多叉树的实现
- //1 广义表
- //2 父指针表示法,适于经常找父结点的应用
- //3 子女链表示法,适于经常找子结点的应用
- //4 左长子,右兄弟表示法,实现比较麻烦
- //5 每个结点的所有孩子用vector保存
- //教训:数据结构的设计很重要,本算法采用5比较合适,同时
- //注意维护剩余样例和剩余属性信息,建树时横向遍历考循环属性的值,
- //纵向遍历靠递归调用
- vector <vector <string> > state;//实例集
- vector <string> item(MAXLEN);//对应一行实例集
- vector <string> attribute_row;//保存首行即属性行数据
- string end("end");//输入结束
- string yes("yes");
- string no("no");
- string blank("");
- map<string,vector < string > > map_attribute_values;//存储属性对应的所有的值
- int tree_size = 0;
- struct Node{//决策树节点
- string attribute;//属性值
- string arrived_value;//到达的属性值
- vector<Node *> childs;//所有的孩子
- Node(){
- attribute = blank;
- arrived_value = blank;
- }
- };
- Node * root;
- //根据数据实例计算属性与值组成的map
- void ComputeMapFrom2DVector(){
- unsigned int i,j,k;
- bool exited = false;
- vector<string> values;
- for(i = 1; i < MAXLEN-1; i++){//按照列遍历
- for (j = 1; j < state.size(); j++){
- for (k = 0; k < values.size(); k++){
- if(!values[k].compare(state[j][i])) exited = true;
- }
- if(!exited){
- values.push_back(state[j][i]);//注意Vector的插入都是从前面插入的,注意更新it,始终指向vector头
- }
- exited = false;
- }
- map_attribute_values[state[0][i]] = values;
- values.erase(values.begin(), values.end());
- }
- }
- //根据具体属性和值来计算熵
- double ComputeEntropy(vector <vector <string> > remain_state, string attribute, string value,bool ifparent){
- vector<int> count (2,0);
- unsigned int i,j;
- bool done_flag = false;//哨兵值
- for(j = 1; j < MAXLEN; j++){
- if(done_flag) break;
- if(!attribute_row[j].compare(attribute)){
- for(i = 1; i < remain_state.size(); i++){
- if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){//ifparent记录是否算父节点
- if(!remain_state[i][MAXLEN - 1].compare(yes)){
- count[0]++;
- }
- else count[1]++;
- }
- }
- done_flag = true;
- }
- }
- if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例
- //具体计算熵 根据[+count[0],-count[1]],log2为底通过换底公式换成自然数底数
- double sum = count[0] + count[1];
- double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);
- return entropy;
- }
- //计算按照属性attribute划分当前剩余实例的信息增益
- double ComputeGain(vector <vector <string> > remain_state, string attribute){
- unsigned int j,k,m;
- //首先求不做划分时的熵
- double parent_entropy = ComputeEntropy(remain_state, attribute, blank, true);
- double children_entropy = 0;
- //然后求做划分后各个值的熵
- vector<string> values = map_attribute_values[attribute];
- vector<double> ratio;
- vector<int> count_values;
- int tempint;
- for(m = 0; m < values.size(); m++){
- tempint = 0;
- for(k = 1; k < MAXLEN - 1; k++){
- if(!attribute_row[k].compare(attribute)){
- for(j = 1; j < remain_state.size(); j++){
- if(!remain_state[j][k].compare(values[m])){
- tempint++;
- }
- }
- }
- }
- count_values.push_back(tempint);
- }
- for(j = 0; j < values.size(); j++){
- ratio.push_back((double)count_values[j] / (double)(remain_state.size()-1));
- }
- double temp_entropy;
- for(j = 0; j < values.size(); j++){
- temp_entropy = ComputeEntropy(remain_state, attribute, values[j], false);
- children_entropy += ratio[j] * temp_entropy;
- }
- return (parent_entropy - children_entropy);
- }
- int FindAttriNumByName(string attri){
- for(int i = 0; i < MAXLEN; i++){
- if(!state[0][i].compare(attri)) return i;
- }
- cerr<<"can't find the numth of attribute"<<endl;
- return 0;
- }
- //找出样例中占多数的正/负性
- string MostCommonLabel(vector <vector <string> > remain_state){
- int p = 0, n = 0;
- for(unsigned i = 0; i < remain_state.size(); i++){
- if(!remain_state[i][MAXLEN-1].compare(yes)) p++;
- else n++;
- }
- if(p >= n) return yes;
- else return no;
- }
- //判断样例是否正负性都为label
- bool AllTheSameLabel(vector <vector <string> > remain_state, string label){
- int count = 0;
- for(unsigned int i = 0; i < remain_state.size(); i++){
- if(!remain_state[i][MAXLEN-1].compare(label)) count++;
- }
- if(count == remain_state.size()-1) return true;
- else return false;
- }
- //计算信息增益,DFS构建决策树
- //current_node为当前的节点
- //remain_state为剩余待分类的样例
- //remian_attribute为剩余还没有考虑的属性
- //返回根结点指针
- Node * BulidDecisionTreeDFS(Node * p, vector <vector <string> > remain_state, vector <string> remain_attribute){
- //if(remain_state.size() > 0){
- //printv(remain_state);
- //}
- if (p == NULL)
- p = new Node();
- //先看搜索到树叶的情况
- if (AllTheSameLabel(remain_state, yes)){
- p->attribute = yes;
- return p;
- }
- if (AllTheSameLabel(remain_state, no)){
- p->attribute = no;
- return p;
- }
- if(remain_attribute.size() == 0){//所有的属性均已经考虑完了,还没有分尽
- string label = MostCommonLabel(remain_state);
- p->attribute = label;
- return p;
- }
- double max_gain = 0, temp_gain;
- vector <string>::iterator max_it = remain_attribute.begin();
- vector <string>::iterator it1;
- for(it1 = remain_attribute.begin(); it1 < remain_attribute.end(); it1++){
- temp_gain = ComputeGain(remain_state, (*it1));
- if(temp_gain > max_gain) {
- max_gain = temp_gain;
- max_it = it1;
- }
- }
- //下面根据max_it指向的属性来划分当前样例,更新样例集和属性集
- vector <string> new_attribute;
- vector <vector <string> > new_state;
- for(vector <string>::iterator it2 = remain_attribute.begin(); it2 < remain_attribute.end(); it2++){
- if((*it2).compare(*max_it)) new_attribute.push_back(*it2);
- }
- //确定了最佳划分属性,注意保存
- p->attribute = *max_it;
- vector <string> values = map_attribute_values[*max_it];
- int attribue_num = FindAttriNumByName(*max_it);
- new_state.push_back(attribute_row);
- for(vector <string>::iterator it3 = values.begin(); it3 < values.end(); it3++){
- for(unsigned int i = 1; i < remain_state.size(); i++){
- if(!remain_state[i][attribue_num].compare(*it3)){
- new_state.push_back(remain_state[i]);
- }
- }
- Node * new_node = new Node();
- new_node->arrived_value = *it3;
- if(new_state.size() == 0){//表示当前没有这个分支的样例,当前的new_node为叶子节点
- new_node->attribute = MostCommonLabel(remain_state);
- }
- else
- BulidDecisionTreeDFS(new_node, new_state, new_attribute);
- //递归函数返回时即回溯时需要1 将新结点加入父节点孩子容器 2清除new_state容器
- p->childs.push_back(new_node);
- new_state.erase(new_state.begin()+1,new_state.end());//注意先清空new_state中的前一个取值的样例,准备遍历下一个取值样例
- }
- return p;
- }
- void Input(){
- string s;
- while(cin>>s,s.compare(end) != 0){//-1为输入结束
- item[0] = s;
- for(int i = 1;i < MAXLEN; i++){
- cin>>item[i];
- }
- state.push_back(item);//注意首行信息也输入进去,即属性
- }
- for(int j = 0; j < MAXLEN; j++){
- attribute_row.push_back(state[0][j]);
- }
- }
- void PrintTree(Node *p, int depth){
- for (int i = 0; i < depth; i++) cout << '\t';//按照树的深度先输出tab
- if(!p->arrived_value.empty()){
- cout<<p->arrived_value<<endl;
- for (int i = 0; i < depth+1; i++) cout << '\t';//按照树的深度先输出tab
- }
- cout<<p->attribute<<endl;
- for (vector<Node*>::iterator it = p->childs.begin(); it != p->childs.end(); it++){
- PrintTree(*it, depth + 1);
- }
- }
- void FreeTree(Node *p){
- if (p == NULL)
- return;
- for (vector<Node*>::iterator it = p->childs.begin(); it != p->childs.end(); it++){
- FreeTree(*it);
- }
- delete p;
- tree_size++;
- }
- int main(){
- Input();
- vector <string> remain_attribute;
- string outlook("Outlook");
- string Temperature("Temperature");
- string Humidity("Humidity");
- string Wind("Wind");
- remain_attribute.push_back(outlook);
- remain_attribute.push_back(Temperature);
- remain_attribute.push_back(Humidity);
- remain_attribute.push_back(Wind);
- vector <vector <string> > remain_state;
- for(unsigned int i = 0; i < state.size(); i++){
- remain_state.push_back(state[i]);
- }
- ComputeMapFrom2DVector();
- root = BulidDecisionTreeDFS(root,remain_state,remain_attribute);
- cout<<"the decision tree is :"<<endl;
- PrintTree(root,0);
- FreeTree(root);
- cout<<endl;
- cout<<"tree_size:"<<tree_size<<endl;
- return 0;
- }
输入的训练数据如下
- Day Outlook Temperature Humidity Wind PlayTennis
- 1 Sunny Hot High Weak no
- 2 Sunny Hot High Strong no
- 3 Overcast Hot High Weak yes
- 4 Rainy Mild High Weak yes
- 5 Rainy Cool Normal Weak yes
- 6 Rainy Cool Normal Strong no
- 7 Overcast Cool Normal Strong yes
- 8 Sunny Mild High Weak no
- 9 Sunny Cool Normal Weak yes
- 10 Rainy Mild Normal Weak yes
- 11 Sunny Mild Normal Strong yes
- 12 Overcast Mild High Strong yes
- 13 Overcast Hot Normal Weak yes
- 14 Rainy Mild High Strong no
- end
程序输出决策树如下
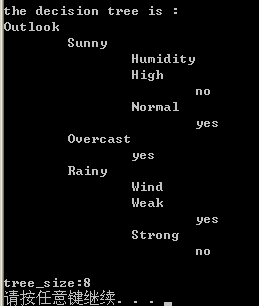
可以用图形表示为
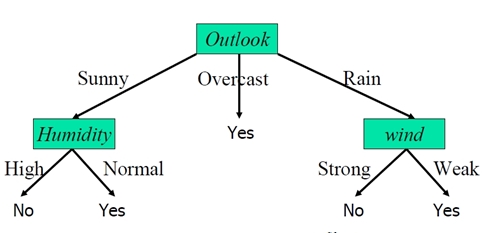
有了决策树后,就可以根据气候条件做预测了
例如如果气候数据是{Sunny,Cool,Normal,Strong} ,根据决策树到左侧的yes叶节点,可以判定会去游泳。
另外在编写这个程序时在数据结构的设计上面走了弯路,多叉树的实现有很多方法,本算法采用每个结点的所有孩子用vector保存比较合适,同时注意维护剩 余样例和剩余属性信息,建树时横向遍历靠循环属性的值,纵向遍历靠递归调用 ,总体是DFS,树和图的遍历在编程时经常遇到,得熟练掌握。程序有些地方的效率还得优化,有不足的点地方还望大家拍砖。




