【转】Robust regression(稳健回归)
Robust regression(稳健回归)
语法
b=robustfit(X,y)
b=robustfit(X,y,wfun,tune)
b=robustfit(X,y,wfun,tune,const)
[b,stats]=robustfit(...)
描述
b=robustfit(X,y) 通过执行稳健回归来估计线性模型y=Xb,并返回一个由回归系数组成的向量b。X是一个n*p预测变量矩阵,y是一个n*1观测向量。计算使用的方法是加 上bisquare加权函数的迭代重加权最小二乘法。默认的情况下,robustfit函数把全1的一个列向量添加进X中,此列向量与b中第一个元素的常 数项对应。注意不能直接对X添加一个全1的列向量。可以在下面的第三个描述中通过改变变量“const”来更改robustfit函数的操作。 robustfit函数把X或y中的NaNs作为一个缺省值,接着把它删除。
b=robustfit(X,y,wfun,tune) 增加了一个加权函数“wfun”和常数“tune”。“tune”是一个调节常数,其在计算权重之前被分成残差向量,如果“wfun”被指定为一个函数, 那么“tune”是必不可少的。权重函数“wfun”可以为下表中的任何一个权重函数:
| 权重函数(Weight Function) | 等式(Equation) | 默认调节常数(Default Tuning Constant) |
|---|---|---|
| 'andrews' | w = (abs(r)<pi) .* sin(r) ./ r | 1.339 |
| 'bisquare' (default) | w = (abs(r)<1) .* (1 - r.^2).^2 | 4.685 |
| 'cauchy' | w = 1 ./ (1 + r.^2) | 2.385 |
| 'fair' | w = 1 ./ (1 + abs(r)) | 1.400 |
| 'huber' | w = 1 ./ max(1, abs(r)) | 1.345 |
| 'logistic' | w = tanh(r) ./ r | 1.205 |
| 'ols' | 传统最小二乘估计 (无权重函数) | 无 |
| 'talwar' | w = 1 * (abs(r)<1) | 2.795 |
| 'welsch' | w = exp(-(r.^2)) | 2.985 |
b=robustfit(X,y,wfun,tune,const)增加一个“const”控制模式内是否包含一个常数项,默认为包含(on)。
[b,stats]=robustfit(...)返回一个包含一下域的STATS结构。
'ols_s' sigma estimate (rmse) from least squares fit
'robust_s' robust estimate of sigma
'mad_s' MAD estimate of sigma; used for scaling
residuals during the iterative fitting
's' final estimate of sigma, the larger of robust_s
and a weighted average of ols_s and robust_s
'se' standard error of coefficient estimates
't' ratio of b to stats.se
'p' p-values for stats.t
'covb' estimated covariance matrix for coefficient estimates
'coeffcorr' estimated correlation of coefficient estimates
'w' vector of weights for robust fit
'h' vector of leverage values for least squares fit
'dfe' degrees of freedom for error
'R' R factor in QR decomposition of X matrix
'robust_s' robust estimate of sigma
'mad_s' MAD estimate of sigma; used for scaling
residuals during the iterative fitting
's' final estimate of sigma, the larger of robust_s
and a weighted average of ols_s and robust_s
'se' standard error of coefficient estimates
't' ratio of b to stats.se
'p' p-values for stats.t
'covb' estimated covariance matrix for coefficient estimates
'coeffcorr' estimated correlation of coefficient estimates
'w' vector of weights for robust fit
'h' vector of leverage values for least squares fit
'dfe' degrees of freedom for error
'R' R factor in QR decomposition of X matrix
The ROBUSTFIT function estimates the variance-covariance matrix of the coefficient estimates as V=inv(X'*X)*STATS.S^2. The standard errors and correlations are derived from V.
matlab例子:
x = (1:10)';
y = 10 - 2*x + randn(10,1); y(10) = 0;
y = 10 - 2*x + randn(10,1); y(10) = 0;
使用原始最小二乘估计和稳健回归估计结果如下:
bls = regress(y,[ones(10,1) x])
bls =
7.2481
-1.3208
bls =
7.2481
-1.3208
brob = robustfit(x,y)
brob =
9.1063
-1.8231
brob =
9.1063
-1.8231
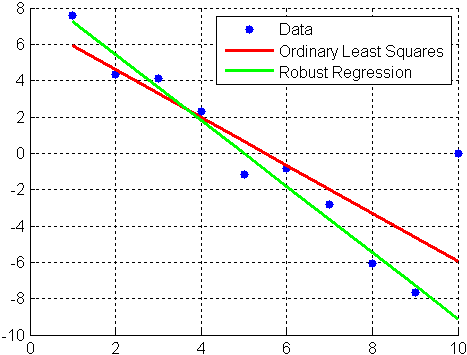
显示结果如下:
scatter(x,y,'filled'); grid on; hold on
plot(x,bls(1)+bls(2)*x,'r','LineWidth',2);
plot(x,brob(1)+brob(2)*x,'g','LineWidth',2)
legend('Data','Ordinary Least Squares','Robust Regression')
plot(x,bls(1)+bls(2)*x,'r','LineWidth',2);
plot(x,brob(1)+brob(2)*x,'g','LineWidth',2)
legend('Data','Ordinary Least Squares','Robust Regression')
一个来自网的例子的matlab实现:
估计: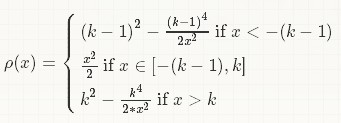 (K>0)
(K>0)
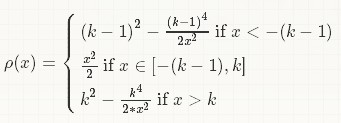 (K>0)
(K>0)matlab实现代码:
function wf=robust(x,y,k)
% find starting values using Ordinary Least Squares
w = x\y;
r = y - x*w;
scale=1;
%optional I can compute the scale using MED
% scale = median(abs(r - median(r)))/0.6745;
cvg = 1;%convergence
while (cvg > 1e-5)
r = r/scale;
wf = w; %save w
WH=wfun(r,k);%diff(rho(xc)/x)
% do weighted least-squares
yst = y.*sqrt(WH);
xst = matmul(x,sqrt(WH));
w = xst\yst;
%the new residual
r = y - x*w;
% compute the convergence
cvg = max(abs(w-wf)./abs(wf));
end;
function W=wfun(r,k)
W=zeros(length(r),1);
for i=1:length(r)
if (r(i)>=-(k-1)) && (r(i)<=k)
W(i)=1;
elseif r(i)<-(k-1)
W(i)=(k-1)^4/(r(i)^4);
else
W(i)=k^4/(r(i)^4);
end
end
% find starting values using Ordinary Least Squares
w = x\y;
r = y - x*w;
scale=1;
%optional I can compute the scale using MED
% scale = median(abs(r - median(r)))/0.6745;
cvg = 1;%convergence
while (cvg > 1e-5)
r = r/scale;
wf = w; %save w
WH=wfun(r,k);%diff(rho(xc)/x)
% do weighted least-squares
yst = y.*sqrt(WH);
xst = matmul(x,sqrt(WH));
w = xst\yst;
%the new residual
r = y - x*w;
% compute the convergence
cvg = max(abs(w-wf)./abs(wf));
end;
function W=wfun(r,k)
W=zeros(length(r),1);
for i=1:length(r)
if (r(i)>=-(k-1)) && (r(i)<=k)
W(i)=1;
elseif r(i)<-(k-1)
W(i)=(k-1)^4/(r(i)^4);
else
W(i)=k^4/(r(i)^4);
end
end
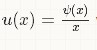 ,其中
,其中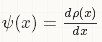 。并且
。并且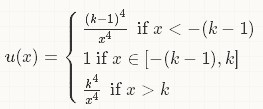 。
。另外,http://blog.csdn.net/abcjennifer/article/details/7449435#(M-estimator M估计法 用于几何模型建立)
博客中对M估计法有蛮好的解释。


