博客作业—图

1.学习总结

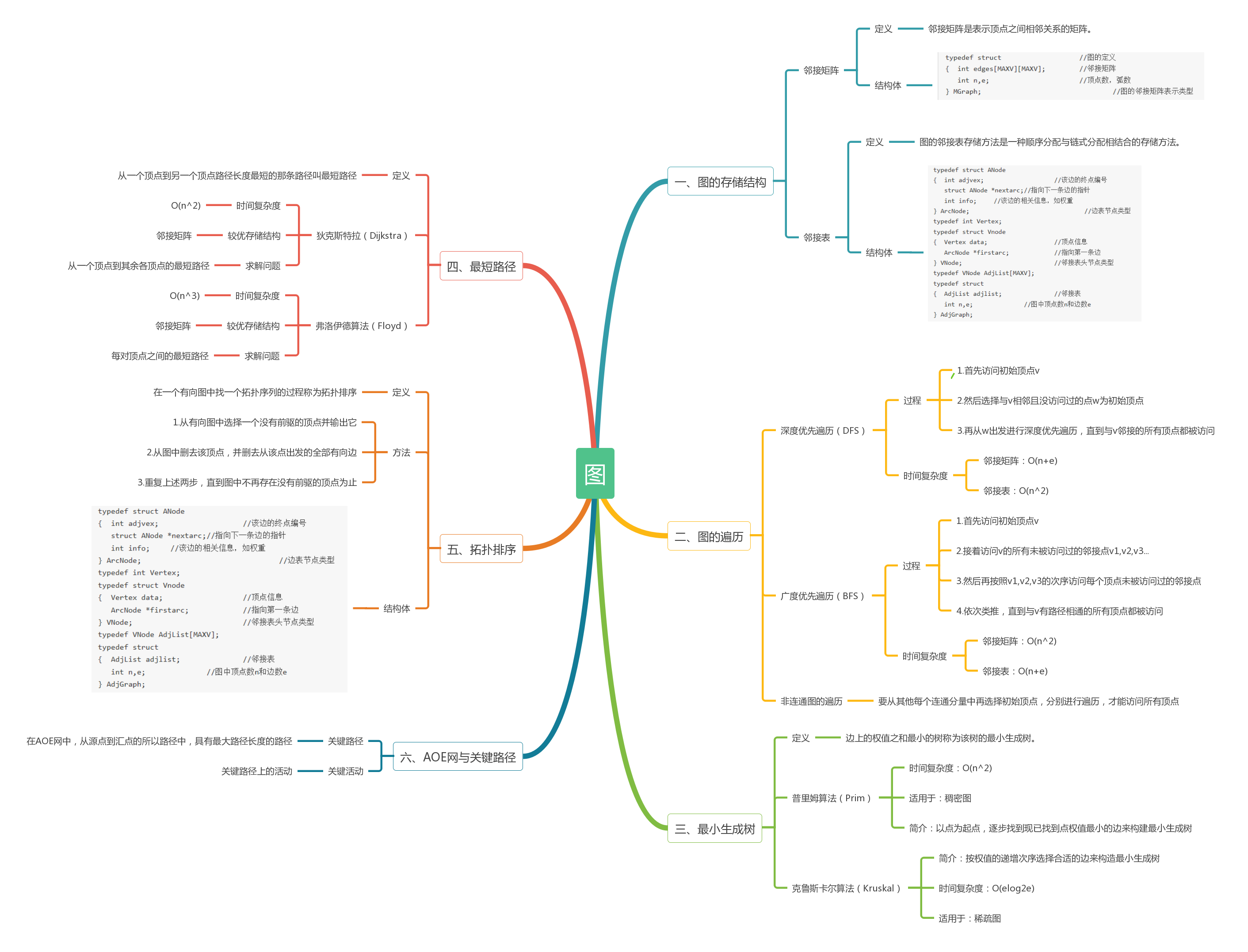
1.1图的思维导图

1.2 图学习体会

• 深度遍历算法：深度遍历的算法是较好理解的，可我写代码时还是习惯于照书敲，明明理解该算法的意思可要真正写起代码来还是有点困难。深度遍历核心是从一个顶点找到下一个顶点，程序中调用递归。
• 广度遍历算法：广度遍历核心在于从一个点出发，遍历这个点所有的邻接点之后再依次遍历它的邻接点 ，程序中用到了队列的相关内容。                 
• Prim和Kruscal算法：刚开始学习这两种算法时我总会将它们混淆，经过较多练习后总算将二者区分。这两种算法用于寻找最小生成树，求最短路径；它们的核心是并查集；一个是选点，一个是选边；当题中边的数目较为复杂时，选用prim算法；一般性问题，可选相对容易理解的kruscal算法。
• Dijkstra算法：这一算法主要用于求解的问题是从一个顶点到其余各顶点的最短路径，目前我还没有在代码中使用过这种算法。
• 拓扑排序算法：针对有向无环图的排序算法，依次找没有前驱的顶点，找到后输出并删去该顶点及从该顶点出发的全部有向边，代码中用到栈。

2.PTA实验作业

2.1 题目1：7-1 图着色问题

2.2 设计思路（伪代码或流程图）

定义a[max][max]表示边，若两点之间有边，则为1，否则为0；
V为顶点数；c[max]表示各顶点颜色;b[max]表示各颜色数目,初始为0;sum统计颜色总数;
for i=0 to V{
输入c[i];
  b[c[i]]++;
 if(b[c[i]]等于1）
 sum++;}
  if(sum不等于指定颜色数）
     输出 No;
  else if(a[i][j]等于1且i,j两点颜色相同)
     输出 No;
  else
     输出 Yes;

2.3 代码截图

2.4 PTA提交列表说明

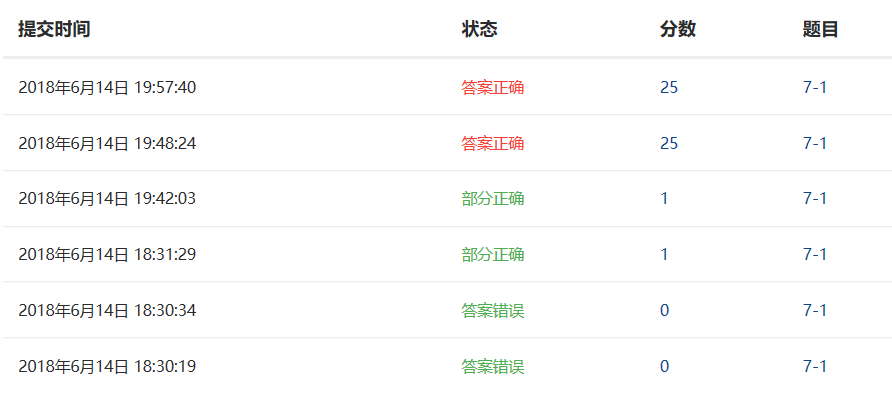
前面几次提交没成功的原因猜测是没有用dfs遍历。具体错误列表如下：

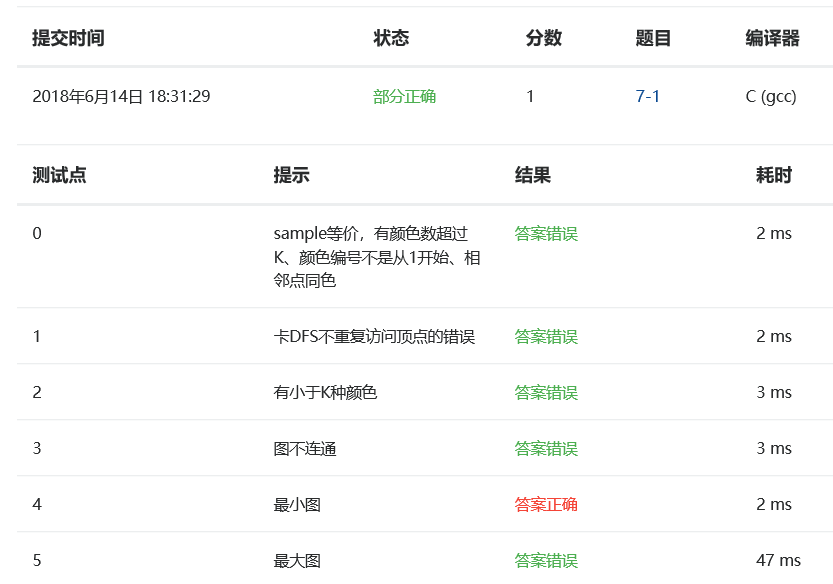
在看到测试点1后我试着用dfs算法将顶点遍历了一遍之后就答案正确了。

2.1 题目2：7-2 排座位

2.2 设计思路（伪代码或流程图）

定义数组enemy[][]记录敌人关系，若是敌人，则为1，否则为0；
建立并查集f[],只要两个人有朋友关系不管是直接还是间接都会保存在同一个集合中。
int main(){
输入宾客及敌友关系；
建立f[]以及enemy[][];
while(K--){
输入两宾客；
if(调用并查集查找两宾客有朋友关系)  flag1等于1；
if(用enemy[][]判断出两个人是敌人关系)  flag2等于1;
据题意判断flag1与flag2应满足关系输出四种情况；
}
end while
}

2.3 代码截图

2.4 PTA提交列表说明

第一次提交出错的原因是输出四种情况对应的关系没有判断清楚，具体是输出"OK but..."这里出错：

 

改正如下：

2.1 题目3：7-4 公路村村通

2.2 设计思路（伪代码或流程图）

定义数组a[][]记录边的权值关系，初始值为inf;
定义变量min表示每条道路最低预算;变量sum表示最低成本 
    for i=1 to n
        dis[i]=a[1][i]; 
    end for 
    for i=2 to n{ 
       min置为inf;
    for j=1 to n
        if (顶点未被访问且该边权值小于min) {
            最低预算min置为该边权值;
            记录最近顶点的编号flag； 
        }
            sum累加最低成本 
            flag顶点标记已访问 
            for j=1 to n
                修改数组dis}
    end for
   if(sum值越界即表示不连通）输出-1；
   else 输出 sum的值；

2.3 代码截图

2.4 PTA提交列表说明

这一题我提交了很多遍，前期一直不对，检查了很多遍一直觉得并没有什么问题，到最后终于发现是在一个非常基础的点上出错，就是在给数组赋初值这一处出现错误导致一直提交答案不正确。

错误列表如下：

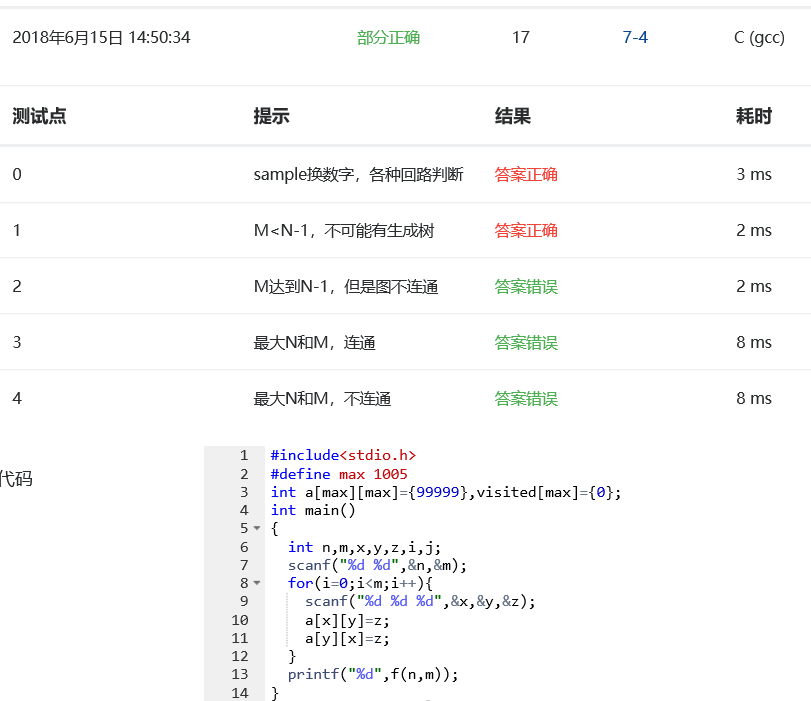
在第三行处就已经出现错误，如果写成a[max][max]={99999}，那么这是表示a[0][0]的值为99999，其他的值其实是没有赋初值的，后来我将其改成：

3.截图本周题目集的PTA最后排名

本次题目集总分：310分

3.1 PTA排名

3.2 我的总分：225分

4. 阅读代码

题目：完美网络

Problem Description

完美网络是连通网络的基础上要求去掉网络上任意一条线路，网络仍然是连通网络。求一个连通网络要至少增加多少条边可以成为完美网络。

Input

第一行输入一个数T代表测试数据个数（T<=20）。每个测试数据第一行2个数n,m 分别代表网络基站数和基站间线路数。基站的序号为从1到n。接下来m行两个数代表x,y 代表基站x,y间有一条线路。 
(0 < n < m < 10000)

Output

对于每个样例输出最少增加多少线路可以成为完美网络。每行输出一个结果。

Example Input

2 
3 1 
1 2 
3 2 
1 2 
2 3

Example Output

2 
1

 代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>   
using namespace std;
int main()
{
    int T,n,m,x,y;  
    cin>>T;  
    int str[100010];  
    while(T--)  
    {  
        memset(str,0,sizeof(str));  
        priority_queue<int,vector<int>,greater<int > >q;//建立队列  
        cin>>n>>m;  
        while(m--)  
        {  
            cin>>x>>y;  
            str[x]++;//记录输入的点的周围的边数
            str[y]++;//上同  
        }  
        sort(str+1,str+n+1);//从小到大排序  
        for(int i=1; i<=n; i++)  
        {  
            if(str[i]<2)  
                q.push(str[i]);//说明需要加边，所以进入队列  
            else  
                break;//若有一个大于等于2,后面的肯定大于等于2,因为已经排序了  
        }  
        int a,b;  
        int c=0;//要加的边数  
        while(q.size()>=2)//只有队列中有两个以上元素才可以进行加边  
        {  
            a=q.top();//拿出第一个节点  
            q.pop();//删除第一个节点  节点已经被变量a记录 删除以便记录接下来的点
            b=q.top();//拿出第一个节点  
            q.pop();//删除第一个节点  
            a++;  //加边
            b++;  //加边
            c++;//边数加1
            if(a<2)  
                q.push(a);  
            if(b<2)  
                q.push(b);  
        }  
        if(q.empty()!=true)//若只有一个元素，首先肯定不是单一存在的，所以边数加1  
        {  
            c++;  
        }  
        printf("%d\n",c);  
    }  

    return 0;  
}  

分析：这篇代码用到了有向图的强连通分量思想，我认为代码的思路值得我学习，它的主要思路是：如果所有的点，都有两条边，那么它就是连通的，不用再考虑加边问题。 例如 1 2 3。 1有两条边，分别连通2和3； 2有两条边，分别连通1和3； 3有两条边，分别连通1和2； 那么这就是连通的。读题时将题意简化有助于我们解题，这是我目前比较欠缺的能力，总是不明白该从何入手，今后需要多加练习。