Xilinx 常用模块汇总(verilog)【02】
作者:桂。
时间:2018-05-08 18:35:56
链接:http://www.cnblogs.com/xingshansi/p/9010282.html
【本文遗留几处细节问题,待闲下来解决。 其中多处涉及原语,以后若有需要,进一步了解可参考文档:hdl.pdf + CLB.pdf。】
一、模块汇总
- 13- 4点FFT(fft4)
路径:印象笔记0019/012
基4原语实现。4点FFT变换(其中时域、频域 均为复数信号):
核心代码:
dat_add_0_r[0] <= $signed(dat_r[0]) + $signed(dat_r[2]); dat_add_0_r[1] <= $signed(dat_r[1]) + $signed(dat_r[3]); dat_add_0_r[2] <= $signed(dat_r[0]) - $signed(dat_r[2]); dat_add_0_r[3] <= $signed(dat_i[1]) - $signed(dat_i[3]); dat_add_0_i[0] <= $signed(dat_i[0]) + $signed(dat_i[2]); dat_add_0_i[1] <= $signed(dat_i[1]) + $signed(dat_i[3]); dat_add_0_i[2] <= $signed(dat_i[0]) - $signed(dat_i[2]); dat_add_0_i[3] <= $signed(dat_r[3]) - $signed(dat_r[1]); dat_add_1_r[0] <= $signed(dat_add_0_r[0]) + $signed(dat_add_0_r[1]); dat_add_1_r[1] <= $signed(dat_add_0_r[2]) + $signed(dat_add_0_r[3]); dat_add_1_r[2] <= $signed(dat_add_0_r[0]) - $signed(dat_add_0_r[1]); dat_add_1_r[3] <= $signed(dat_add_0_r[2]) - $signed(dat_add_0_r[3]); dat_add_1_i[0] <= $signed(dat_add_0_i[0]) + $signed(dat_add_0_i[1]); dat_add_1_i[1] <= $signed(dat_add_0_i[2]) - $signed(dat_add_0_i[3]); dat_add_1_i[2] <= $signed(dat_add_0_i[0]) - $signed(dat_add_0_i[1]); dat_add_1_i[3] <= $signed(dat_add_0_i[2]) + $signed(dat_add_0_i[3]);
四个数的加减可在3个数加减的基础上扩展(3个数相加),借助1- adder_3op的思路,4个数相加拆解:3个数相加 + 1个数,具体参考:印象笔记:0019/014。同样可以实现FFT/IFFT。【至于3个数加减的优势,本质上应该取决于CLB特性。】
- 14- 8点FFT(fftr8)
1) 基2原语实现
印象笔记:0019/012,fft_eight.sv
2) 基2、基4原语实现【tb文件存在问题,待排查。】
8点可在4点FFT的基础上进行基2的求解,理论基础:
data = randi(20,[1,8]); RefFFT = fft(data); data_odd = data(1:2:end); data_even = data(2:2:end); wk = exp(-1j*2*pi/8*[0:3]); fft_connect = fft(data_even).*wk+fft(data_odd); [fft_connect,sum(data.*[(-1).^[0:7]]),fliplr(conj(fft_connect(2:end)));RefFFT]
二者完全等价。即8点FFT比4点FFT多了复数相乘、复数相加的基本操作。对于8点的旋转因子: exp(-1j*2*pi/8*[0:3])近有sqrt(2),利用18bits*25bits乘法器,sqrt(2)/2定义为 parameter wk = b = 25'd11863283; //2^0.5/2*2^24,借助rtldelay延拍,利用乘法即可求解。
3)IP核实现
- 15- 32点FFT(fftr32)
基2、基4混合基原语实现。基本思路同8点FFT类似。
路径:印象笔记:0019/012,涉及到分时复用,待进一步细化。
- 16- N点FFT(N为2整次幂)
参数化编程。【暂未编写】
目前的思路是:
1)如果是4的整次幂,则基4实现;2)如果不是4的整次幂,N/2基4实现,最后一级基2实现。
基4递归的思路参考二、FFT原理简述-Part.B
二、FFT原理简述
本段文字参考:程佩清《数字信号处理》。
A-基2FFT
DFT与IDFT操作:
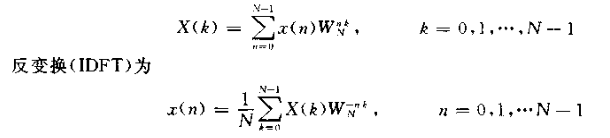
快速实现分为DIF、DIT(T:time , F:frequency)两种角度,
DIT2原理:
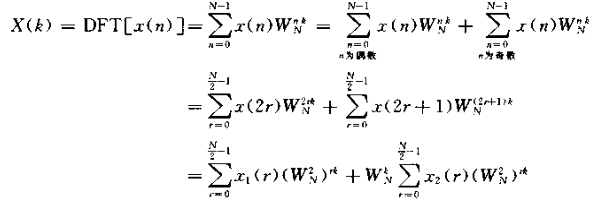
实现流图:
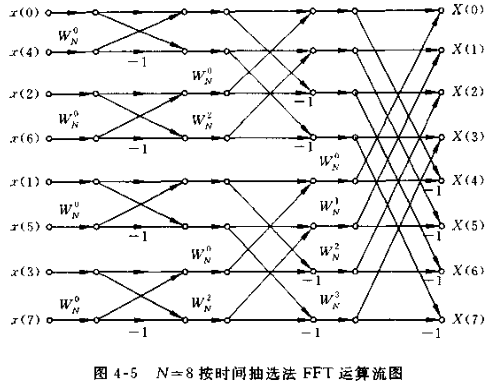
DIF2原理:

流图:
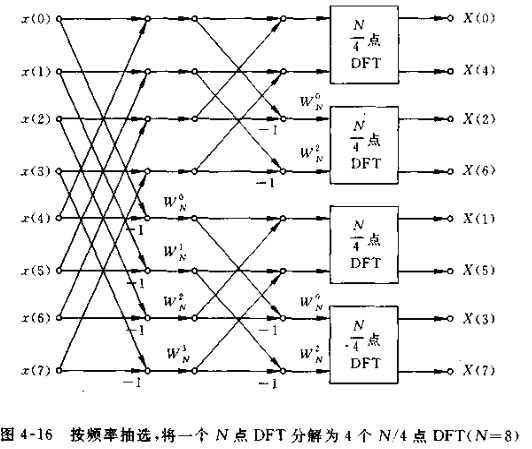
B-基4FFT
此处仅记录DIF4,具体可参考基4FFT实现。
matlab仿真:
clear;
a=0:4095;x=sin(2*pi/3*a)+sin(2*pi/4*a)+sin(2*pi/5*a); %输入三频率信号
subplot(2,1,1),plot(x);
axis([0 4096 -3 3]),title('时域信号波形');
subplot(2,2,3),plot(abs(fft(x)));
axis([0 4096 0 2500]),title('系统 FFT 计算出的频谱');
N=4096; %N 点 DFT,N 为 4 的整数次幂
L=log(N)/log(4); %4 点 DFT 分解级数
Wn=exp(-2j*pi/N); %旋转因子
temp=zeros(1,N); %定义中间临时数组
%%%4 进制逆序排序%%%
%这里通过对四进制数 n,先每相邻两位翻转,再将两位合成一组,相邻两组翻转,直到整体翻转一次为止,即可得到 4 进制逆序排序。
n=0:N-1;
screen=ones(1,N);
n=bitor(bitand(n,screen*hex2dec('cccc'))/4,bitand(n,screen*hex2dec('3333'))*4);
n=bitor(bitand(n,screen*hex2dec('f0f0'))/16,bitand(n,screen*hex2dec('0f0f'))*16);
n=bitor(bitand(n,screen*hex2dec('ff00'))/256,bitand(n,screen*hex2dec('00ff'))*256);
n=n/4^(8-L)+1;
for n1=1:N
temp(n(n1))=x(n1);
end
x=temp;
%%%基 4FFT%%%
%这部分根据递推公式以 4 点 DFT 为基本单元,反复进行 L 级迭代,最终得到 N 点 DFT 值。
for l=1:L %运算级循环
group_cont_2=4^(L-l); %第 l 级数据分组数
group_cont_1=4^(L-l+1); %第 l-1 级数据分组数
group_interval_2=4^l; %第 l 级组间数据间隔个数,也是组内数据个数
group_interval_1=4^(l-1); %第 l-1 级组间数据间隔个数,也是组内数据个数
G=group_cont_2-1; %分组上限
K=group_interval_1-1; %组内数据上限
for g=0:G %每一级中包含的组循环,遍历每一组,计算各组中的数据
for k0=0:K %遍历每一组中的所有数据,计算次级数据
k=k0+g*group_interval_2+1; %每组数据中第一个数据序号
m=group_cont_2*k0; %每一级所乘旋转因子的指数因子
k1=k;k2=k1+group_interval_1;k3=k2+group_interval_1;k4=k3+group_interval_1; %每组数据中四个数据的序号
X1=x(k1);X2=Wn^m*x(k2);X3=Wn^(2*m)*x(k3);X4=Wn^(3*m)*x(k4); %将递推公式中重复计算部分用变量代换,减少运算次数
%根据递推公式计算,结果存储到临时数组 temp
temp(k1)=X1+X2+X3+X4;
temp(k2)=X1-1j*X2-X3+1j*X4;
temp(k3)=X1-X2+X3-X4;
temp(k4)=X1+1j*X2-X3-1j*X4;
end
end
x=temp; %将 temp 中临时存储的第 l 级结果赋值给 x,作为次级运算的输入
end
subplot(2,2,4),plot(abs(x));
axis([0 4096 0 2500]),title('自定义基 4FFT 计算出的频谱');

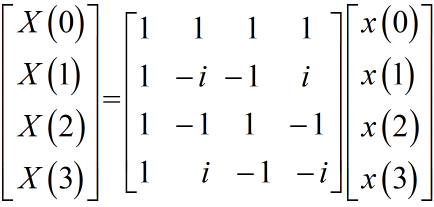



 浙公网安备 33010602011771号
浙公网安备 33010602011771号