复数矩阵分解的拆解思路(矩阵求逆/特征值分解)
作者:桂。
时间:2017-10-26 07:11:02
链接:http://www.cnblogs.com/xingshansi/p/7735016.html
前言
主要记录特征值分解的硬件实现思路。
一、实数矩阵转化
在FPGA运算中,对实数运算通常优于对复数运算。假设C为复数矩阵:C= A+iB;且
C = CH
从而A = AT;B = -BT;若C的奇异值 所对应的奇异向量为u + iv,且满足:
所对应的奇异向量为u + iv,且满足:
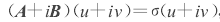
对应有:
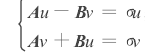
借助矩阵形式表示:
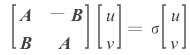
根据A、B的性质,存在:
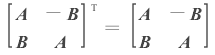
一个NxN的Hermitian矩阵分解,转化为2Nx2N的实对称矩阵分解。
二、Jacobi算法(Givens旋转)
对于对称矩阵:
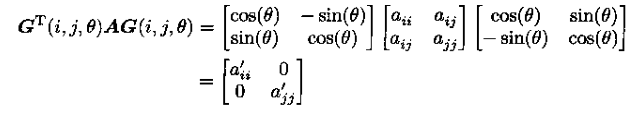
其中Givens参数:
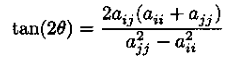
该公式可进一步转化:$tan(2theta) = 2a_{ij}/(a_{jj}-a_{ii})$;theta可以借助cordic算法求解。
此处可以借助Cordic求解角度,也可以利用CORDIC求根号的思路进行sin、cos的计算:
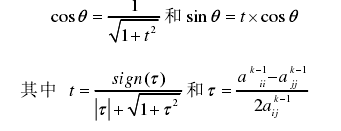
aii= 1; ajj = 3; aij = 1.2; tan_2 = (2*aij/(ajj-aii)); theta = 1/2*atan(tan_2); tao = 1/tan_2; t = sign(tao)/(abs(tao)+sqrt(1+tao.^2)); cos_1 = 1/sqrt(1+t^2) cos_1_new = cos(theta) sin_1 = t/sqrt(1+t^2) sin_1_new = sin(theta)
使用Givens旋转左乘A,可以得到对角阵,右乘同样可以得出。只使用左乘\右乘的Givens旋转称为单边Givens旋转。与之不同,对nxn对称矩阵A同时采用左乘、右乘的方法,称为双边Givens旋转。
具体代码实现,参见:印象笔记-005常用算法-0020Jacobi算法。
借助之前SVD实现矩阵求逆的思路,矩阵求逆的硬件实现,也可以在此基础上直接实现。(此处实对称矩阵,利用:特征向量x特征值取反x特征向量转置,即完成矩阵求逆)
clc;clear all; x = rand(4,100)*20+1i*rand(4,100)*20; R = x*x'/100; A = real(R); B = imag(R); R_cat = [A -B;B A]; [D,V]=Jacobi(R_cat); % V = V'; U_est = V(1:4,1:2:end)+1i*V(5:end,1:2:end); D0 = diag(D); D0 = 1./D0(1:2:end); R_inv = U_est*diag(D0)*U_est'
三、并行拆解思路
对于nxn的矩阵分解,一种思路是寻找矩阵所有非对角元素中绝对值较大者进行双边Jacobi变换,使得该非对角线元素变为0.接着进行第二次变换,直到收敛至精度要求,O(n2)复杂度。
另一种是固定计算顺序的方法(术语:循环Jacobi,cycle Jacobi),简单粗暴且便于在硬件上实现(行/列):
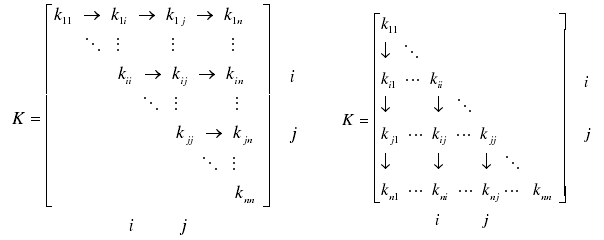
假设矩阵维度为8,经过一次迭代的计算顺序可表示为:

仿真验证参考:Jacobi并行拆解
对于维度为N的矩阵,每一行的N/2个都可以并行,遍历一次(专业术语:Sweep)需要N-1个周期。对于N维度的矩阵,排序的顺序为:
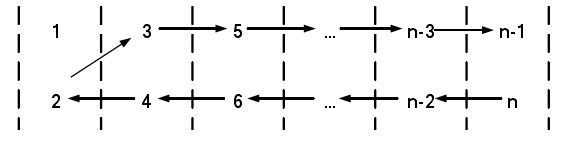
如N = 10,除去1,2追溯到4,3追溯到2,5追溯到3.......依次类推。
S_0:(1,2)-(3,4)-(5,6)-(7,8)-(9,10)
S_1:(1,4)-(2,6)-(3,8)-(5,10)-(7,9)
......
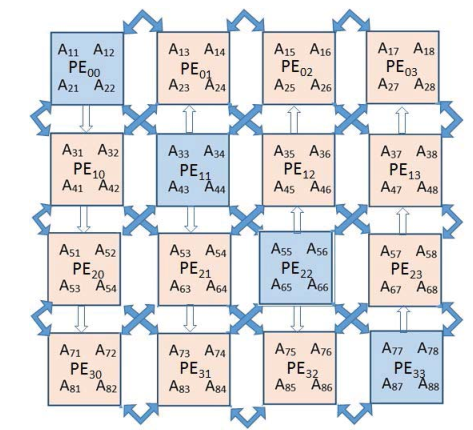
BLV Array for N=8. Data transmission is represented as solid arrows and rotation parameters transmission with unfilled arrows.

