空间谱专题13:联合解算DOA(ML/AP)
其中作者:桂。
时间:2017-10-16 07:51:40
链接:http://www.cnblogs.com/xingshansi/p/7675380.html
前言
主要记录二维测向中,分别利用两个一维阵联合解算的思路。
一、AP算法思想
信号模型:
![]()
对应相关矩阵
![]()
假设噪声为遍历、平稳、空时不相关的零均值高斯随机过程,源信号为未知确定信号:
![]()
高维正态分布表达式:

由概率论可知,几个独立同高斯分布随机过程的概率密度函数为:
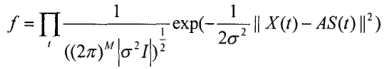
取对数:
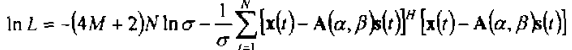
观测向量为X(t),对其求偏导:
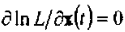
得到信号s的极大似然估计:

再针对方差求偏导:
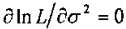
将s的似然估计结果代入原表达式中,方差结果sigma也代入,可以得到:
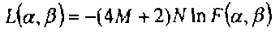
其中
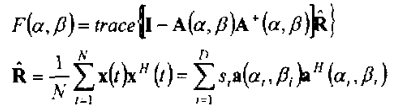
而A+是Moore-Penrose逆:
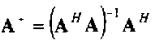
记投影矩阵以及补空间的投影矩阵:


综合上式,可以得出角度最大似然估计:
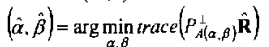
等价于:
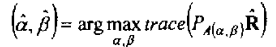
该算法基于统计参数估计的思路,不涉及SVD分解或者相关矩阵求逆,因此对于相干信号理论上仍然适用,从理论的结构来看,由于投影矩阵涉及求逆,且有迭代过程,因此耗费资源过大。
通常该算法可与其他算法结合使用,用于剔除杂峰,主要代码实现:
function [phi_last,theta_last] = MuCalL_2D(x,srcNum,Array,resolution,lambda_c)
%L阵
sub1 = [1:6];
sub2 = [1,7:11];
J = fliplr(eye(length(sub1)));
x1 = x(sub1,:);
x2 = conj(J*x(sub2,:));
[phi,theta,spec1] = MuCalL_647_1D(x1,srcNum,Array(sub1,:),resolution,lambda_c);
[phi2,alpha,spec2] = MuCalL_647_1D(x2,srcNum,Array(sub1,:),resolution,lambda_c);
%
[val1,phi_pos] = findpeaks(spec1,'minpeakdistance',3);
[val,num_phi] = sort(val1,'descend');
[val2,theta_pos] = findpeaks(spec2,'minpeakdistance',3);
[val,num_theta] = sort(val2,'descend');
phi_est = phi(phi_pos(num_phi(1:srcNum)));
theta_est = alpha(theta_pos(num_theta(1:srcNum)));
phi_est = phi_est;
%筛选
snap = size(x,2);
R_all = x*x'/snap;
para_all = perms([1:srcNum]);
theta_all = kron(theta_est,ones(1,size(para_all,1)));
theta_all([2,4]) = theta_all([4,2]);
phi_all = repmat(phi_est,1,size(para_all,1));
theta_all = asin(sin(theta_all/180*pi)./cos(phi_all/180*pi))/pi*180;
im = sqrt(-1);
Dd = [];
for kkk = 1:size(theta_all,2)/srcNum
nshift = ((kkk-1)*srcNum+1):((kkk)*srcNum);
theta_cache = theta_all(nshift)/180*pi;
phi_cache = phi_all(nshift)/180*pi;
Az = [];
for j = 1:srcNum
r = [sin(phi_cache(j)) cos(phi_cache(j))*sin(theta_cache(j)) cos(phi_cache(j))*cos(theta_cache(j))];
r_rep = repmat(r,size(x,1),1);
dis = sum(r_rep.*Array,2);
am = exp(-im*2*pi*dis/lambda_c);
Az = [Az,am];
end
Pb3 = Az*pinv(Az'*Az)*Az';
Dd(kkk) = abs(trace(Pb3*R_all));
end
[valDd,indexDd]=max(Dd);
n_pos = ((indexDd-1)*srcNum+1):((indexDd)*srcNum);
[phi_last,sort_pos] = sort(phi_all(n_pos),'ascend');
theta_last = theta_all(n_pos);
theta_last = theta_last(sort_pos);
二、其他思路(对相干信号适应性较差)



该方法针对ULA(均匀线阵),1)未考虑非均匀线阵NULA情形;2)未考虑相干source情形。
个人分析,该算法可改进(未进一步仿真验证): 对于相干且NULA情形,1)各自平滑,X、Z轴相对位置无严格限制,但X、Z需结构一致;2)求解Rzx,并取对角元素diag(Rzx),结合两个一维测向得出导向矢量:max |a(theta)conj(a(phi)).*diag(Rzx)|。
三、联合解算论文
联立解算的思路:

主要代码实现:
Ax = A(sub1,:);
Ay = A(sub2,:);
%利用T矩阵解算
y_sig = x2;
x_sig = x1;
Ryy = y_sig*y_sig'/snapshot;
Rs_hat = pinv(Ay'*Ay)*Ay'*Ryy*pinv(Ay*Ay')*Ay;%eq.5
Rxy = x_sig*y_sig'/snapshot;
Ay_pieH = pinv(Ay*Ay')*Ay;
Rs_pie = pinv(Ax'*Ax)*Ax'*Rxy*Ay_pieH;%eq.9
%构造T矩阵解算
perm = perms([1:srcNum]);
J = zeros(1,size(perm,1));
for i = 1:size(perm,1)
T = zeros(srcNum);
T(perm(i,:)+[0:srcNum-1]*srcNum) = 1;
J(i) = sum(sum(abs(Rs_pie-T*Rs_hat).^2));
end
[minVal,minPos] = min(J);
phi_est = phi_est(perm(minPos,:));
theta_all = theta_est;
%求解
phi_last = phi_est;
theta_last = asin(sin(theta_all/180*pi)./cos(phi_last/180*pi))/pi*180;
当个数不匹配的时候可参考(个人觉得直接拓展效果也可以,就是配对之前添加一个预处理):



