时域、空域对偶性

厚着脸皮要在同事公众号上写篇文章，尽量浅显、与专业相关，选了这个主题。

---

 一、时域与空域特性

以远场模型（平面波）为例，假设均匀线阵接收的为窄带信号，假设相邻振元间隔为d，入射角为：

从空域坐标来看，相邻振元的间隔为：

等价到时间轴来看，采样点的间距为：，对应时间间隔为：

 

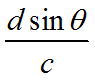
二、时、空域与采样定理

　　A-空域角度理解

相邻振元的相位差为：

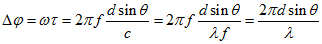
以干涉仪为例，如果存在相位模糊，有

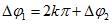
k为非零整数，如果希望不出现相位模糊

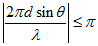
对应扫描边界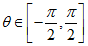，则有

容易证明，同干涉仪一样，均匀线阵谱估计中的导向矢量，如果不满足上面的约束条件，同样会有多峰的问题。

　　B-时域角度理解

前文提到，采样点对应的时间间隔为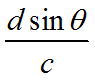，即采样周期。空域均匀线阵对应时域均匀采样，采样频率：

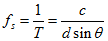
入射信号的频率为：

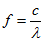
如果采样无混叠，需要满足Nyquist采样定理：

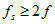
该约束条件等价于：

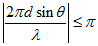
可以看出均匀线阵的相位无模糊对应时域均匀采样的奈奎斯特定理。多说一句，如果是非均匀线阵、圆阵等形式，可以理解成对应维度的非均匀采样；从空域角度理解，非均匀阵列可以解决模糊问题，从时域角度理解，稀疏采样/非均匀采样可以突破奈奎斯特采样定理。

 

三、时、空域及MVDR算法

波束形成主要对感兴趣的方向进行增强/抑制，而谱估计更多是参数估计问题，前者操作多为主动，后者操作多为被动，MVDR算法对二者均适用。这里暂且抛开应用场景，仅从时、空角度理解MVDR的等价性。

接着上文的时域、空域思路，这里先从时域的角度来表述，为了简化均不考虑加窗情形。

　　A-时域角度理解

对于N点均匀采样的信号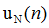，对其进行傅里叶变换：

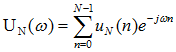
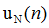的相关函数为：

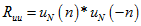
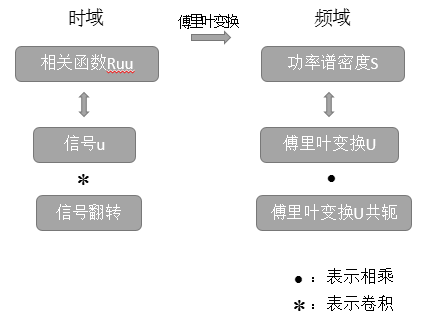
容易证明有如下对应关系：

而相关函数对应的傅里叶变换为功率谱密度，可以求解功率谱密度：

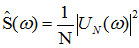
　　B-空域角度理解

 N个均匀线阵接收单元，对应的波束形成为：

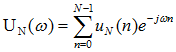
即空域的波束形成可以理解为时域的傅里叶变换，

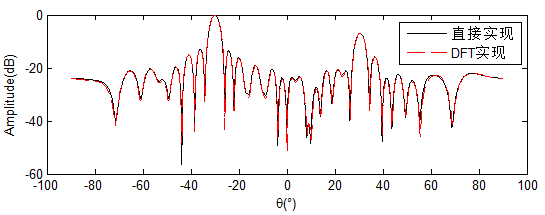
从而空域的功率谱密度可以等价为：

考虑到时域、空域具有等价性，空域的功率谱这么理解是合理的。

现在以常用的MVDR算法来理解这种等价性（MUSIC等谱估计算法的谱与波束形成完全不同，这里仅从时、空等价性上讨论“谱”的概念）：

接收信号：

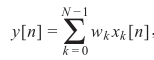
MVDR就是含有等式约束的最优化问题：

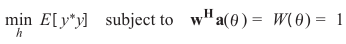
可以求解：

这个时候，如果将最优的w带入y，空域角度理解：y对应就是波束形成的结果。时域角度理解：y对应为傅里叶变换的结果。

通常MVDR的结果为的输出，根据上文分析可知，该结果从时域理解就是功率谱（差一个常数），所以从空域角度称作“谱”其实也是可以被接受的，对应功率（谱）：

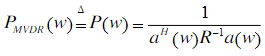
因为这是在空域，为了与时域功率谱的名字加以区别，可以称其为空间谱。

具体空间谱名称怎么由来，本文并没有考证。本文只是提供了一种理解“空间谱”名称的角度，至少MUSIC等算法的“谱”便与此不同，或许MUSIC等算法只是继承了“空间谱”这个名词也未可知。