空间谱专题03：时空特性与采样定理

作者：桂。

时间：2017-08-27  08:07:30

链接：http://www.cnblogs.com/xingshansi/p/7439558.html 

---

 一、一阶无模糊特性

可结合时域、空域对偶性一文来理解。

在DOA ambiguity vs. array configuration for subspace-based DF method 一文，关于first-order ambiguity of arbitrary array for subspace-based DF(direction finding) methods，有以下一般性结论：

定义Eq1. :

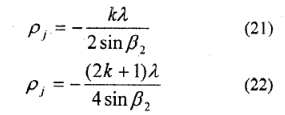
其中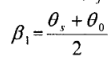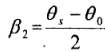，。得出的一般性结论为：

For M elements arbitrary array, the subspace-based DOA estimation will cause the first-order ambiguity in a wide frequency band if and only if there is existing certain angle belta_1, which make the ambiguity factor vector pho satisfy one of the following conditon:

特别地，对于ULA,结论就是孔径＜半波长；

对于UCA：

 

二、空域与时域特性

 给出一维的分析，高维对应高维度的采样定理，类推即可。

相位无模糊，

空间轴视角：空域上就是相位差，对应：

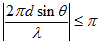
时间轴视角：相邻间隔为dsin（theta），对应时间（采样间隔，即 周期）为dsin(theta)/c，c为光速，从而采样率为：

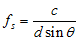
若无混叠采样，则要求信号频率小于等于fs/2(Nyquisist 定理)：

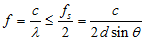
可见得出的结论是一致的。

如果是非均匀线阵NULA，则对应的是非均匀采样理论的知识，这样分析相位模糊问题，可以转化为分析采样以及信号重建的理论问题，后者的资料更多一些。