GM11灰色模型
作者:桂。
时间:2017-08-12 08:34:06
链接:http://www.cnblogs.com/xingshansi/p/7348714.html
前言
灰色模型(Gray model)常用来对数据进行预测,这里简要记录其思路。
一、名称由来
灰色模型(Gray Model),邓聚龙教授1982年提出。
常见系统分类:
- 白色系统是指一个系统的内部特征是完全 已知的,即系统的信息是完全充分的。
- 黑色系统是指一个系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究。
- 灰色系统内的一部分信息是已知的,另一部分信息是未知的,系统内各因素间有不确定的关系。
通常成灰色预测模型为GM(n,h)模型,常用来预测的是GM(1,1):
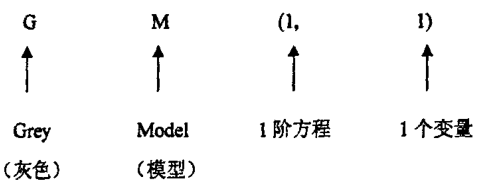
二、算法原理
A-模型建立
有观测序列:

计算一阶累加序列:

其中
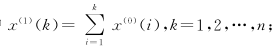

得出参数估计
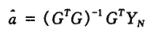
C-序列预测![]()
这里取
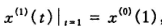
将其带入上面一阶方程解(参数已求出)
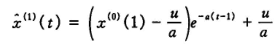 取t为离散值(t = k+1)
取t为离散值(t = k+1)
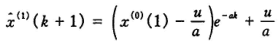 而
而
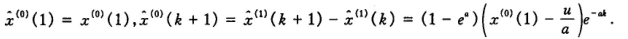
这样便完成了预测。
三、代码实现
主函数
clc;clear all;close all
set(0,'defaultfigurecolor','w');
%{
参考:《离散模型与灰色预测模型建模机理》,谢乃明,刘思峰
本程序主要用来计算根据灰色理论建立的模型的预测值。
应用的数学模型是 GM(1,1)。
原始数据的处理方法是一次累加法。
%}
f = @(t,b)(0.3*t.^2+b+0.3*randn(1,length(t)));%定义待预测函数
t = 0:.2:5;
b = 3;
x0 = f(t,b);
x_pre = GM11(x0);
plot(t,x0,'k',t,x_pre,'r--');
xlabel('时间(年)');
ylabel('幅度');
title('GM11预测模型');
legend('原始数据','预测数据');
GM11的function:
function x_pre = GM11(x0)
x0 = x0(:);
n = length(x0);
x1 = cumsum(x0);
for i = 1:n-1
G(i,1) = -(x1(i)+x1(i+1))/2;
G(i,2) = 1;
end
Y = x0(2:end);
belta = pinv(G'*G)*G'*Y;
a = belta(1);
u = belta(2);
%predict
x_pre1 = zeros(n,1);
x_pre = x_pre1;
for k = 0:n-1
x_pre1(k+1) = (x0(1)-u/a)*exp(-a*k)+u/a;
end
x_pre(1) = x0(1);
for k = 1:n-1
x_pre(k+1) = x_pre1(k+1)-x_pre1(k);
end
结果图:
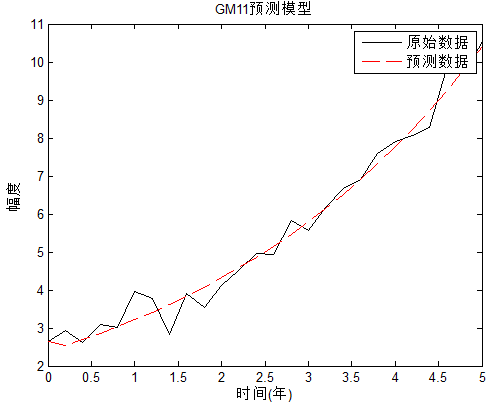

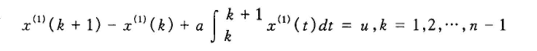

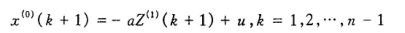
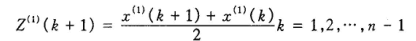
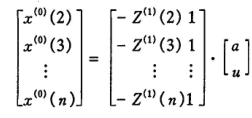
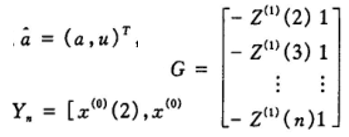 计算均值生成序列:
计算均值生成序列: