多相滤波器
前言
多相滤波器解决的是：多速率问题。
通过降采样、插值来改变信号的输出速率（主要利用Nyquist采样定理，保证不混叠），从而降低数据率，多相滤波器为这类操作提供了实现框架。在满足采样定理的前提下，内插/抽取并配合滤波器使用（防止混叠），可以改变数据的速率。
多相滤波的结构也多用在信道化中（即构建滤波器组），固化系数借助硬件实现快速运算。
一、信道化实现思路
信道化的基本思路为：
clc;clear all;close all
N = 256;
h = firls(N, [0 .2 .25 1], [1 1 0 0],[.001 .0001]);
D = 8;
% PolyPhase Componets
i = 1:length(h);
h_channel = zeros(D,length(h));
im = sqrt(-1);
for j = 1:D
h_channel(j,:) = h.*exp((-im*2*pi*((j-1)*(i-1)))/D);
end
figure(1)
for i = 1:D+1
switch i
case 1
subplot (2,1,1);
plot(abs(fft(h)));
title('Orignal LPF ')
otherwise
subplot (2,1,2)
plot(abs(fft(h_channel(i-1,:))));
hold on;
title('channelize')
end
end
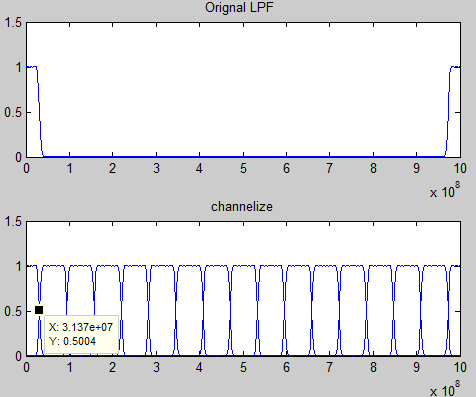
对应频谱图：
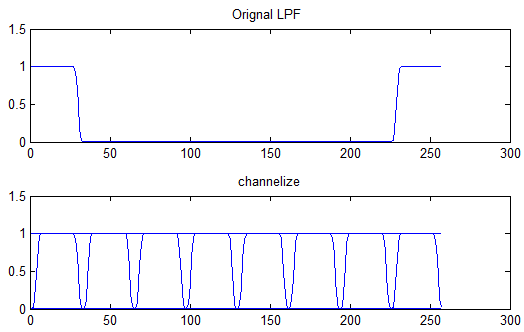
即将频带切分成若个个区域。基于该特性，有信道化的基本思路：
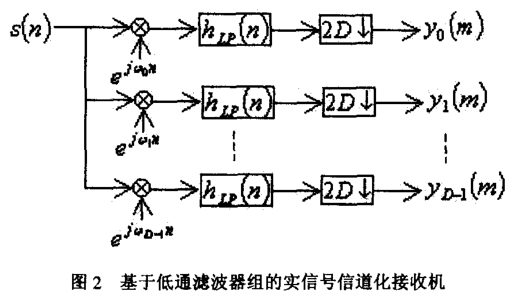
如果是实信号，D信道化之后进行D倍抽取仍然不会有频谱混叠，而经过本振以及低通滤波器之后的信号为复信号，故可以进行2D倍抽取。
可以看出，信道化接收机的抽取器位于滤波器之后，当抽取率D很大或者滤波器阶数较高，计算效率将难以提升，这时候借助多相滤波器便可以优化。
假设LPF：
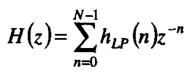
并取Q=N/D，N为滤波器阶数，D为抽取率。则滤波器可重写为：
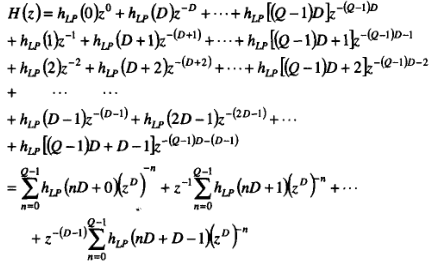
定义：
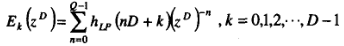
滤波器可重写为：
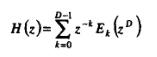
其中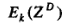
为多相分量，这也是多相滤波器说法的缘由。
第k个信道可写为：
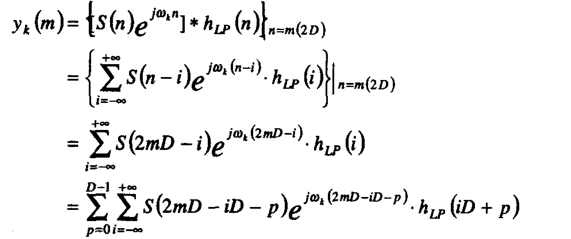
记
有
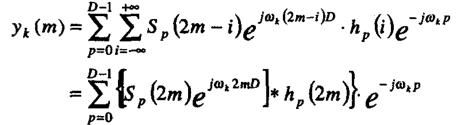
令
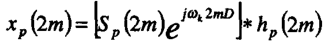
则
进一步取
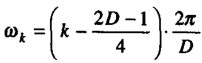
从而有
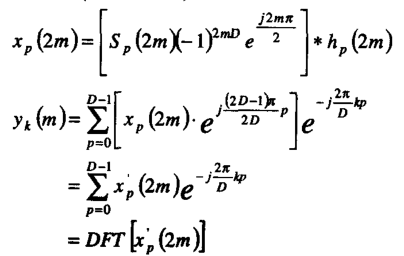
根据这一系列推导，即可得出实信号多相滤波器信道化的实现思路：
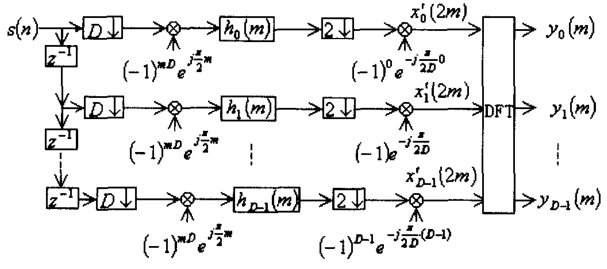
两处相位相乘分别为：
，p = 0,1,...,D-1
二、多相滤波器设计步骤
- 根据指标，确定滤波器类型以及阶数N
- 求解h（n）
- 根据信道个数，并用下式确定多相滤波器：
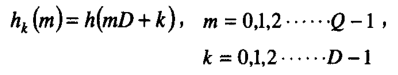
三、复杂度简要分析
以滤波器阶数N=256，抽取率（信道个数）D=16，每个信道输出1个数据，则：
- 基于低通滤波器组的信道化需要乘法：M1 = D x (1+N) = 4112次；
- 基于多相滤波器的信道化需要乘法：M2 = N+2*D+D*log2D = 352次；
多相滤波器的实现思路节约了资源，且便于硬件实现。
四、应用实例
考虑带宽1GHz的情况，如果信道个数为16，则每一个的宽度为1e9/16=62.5e6，考虑到滤波器为实数的共轭对称性，故LPF构造依据：
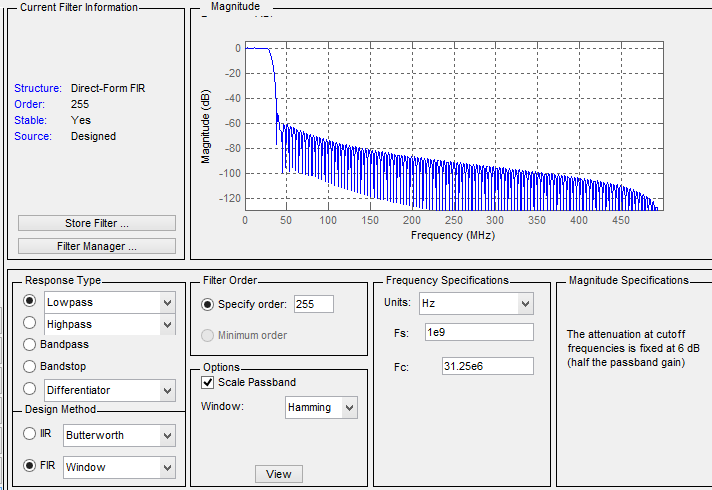
对其进行仿真验证：
输入信号为70MHz的1）余弦信号；2）复指数信号，对于1）理论上应落在2、16两个信道，2）只落在2信道。
clc;clear all;close all
load coef_lpf.mat;
fs = 1e9;
t = 0:1/fs:1e-6;
f0 = 70e6;
sig = sin(2*pi*t*f0);
len = length(sig);
h = coef_lpf;
N = length(h);
D = 16;
y = zeros(D,len);
% PolyPhase Componets
i = 1:length(h);
h_channel = zeros(D,length(h));
im = sqrt(-1);
x_fre = linspace(0,fs,N);
for j = 1:D
h_channel(j,:) = h.*exp((-im*2*pi*((j-1)*(i-1)))/D);
y(j,:) = filter(h_channel(j,:),1,sig);
end
figure()
for i = 1:D+1
switch i
case 1
subplot (2,1,1);
plot(x_fre,abs(fft(h)));
title('Orignal LPF ')
otherwise
subplot (2,1,2)
plot(x_fre,abs(fft(h_channel(i-1,:))));
hold on;
title('channelize')
end
end
x_fre1 = linspace(0,fs,len);
figure()
plot(x_fre1,abs(fft(sig)));
for iter = 1:D
if mod(iter,4) ==1
figure()
j = 1;
end
subplot(4,1,j)
j = j+1;
plot(x_fre1,abs(fft(y(iter,:))));
title(['信道',num2str(iter)]);
end
仿真结果：
信道化结果：
情形一：
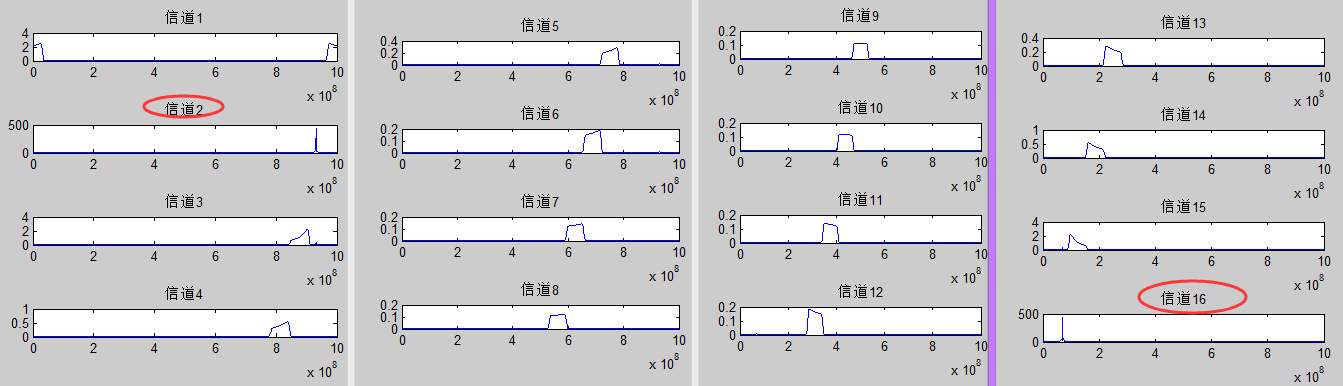
与理论分析相符。
情形二：
sig = exp(-1j*2*pi*t*f0);
信号只在信道2出现：
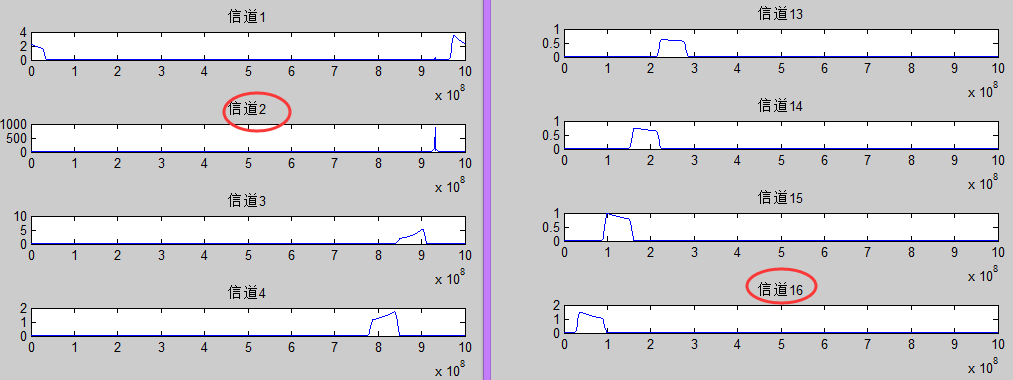
多相滤波的实现思路也非常多，这里仅列举一种：
clc;clear all;close all;
load coef_lpf.mat;
h = coef_lpf;
%%产生信号
fc = 70e6;
c = 3.0e8;
fs = 1e9;
theta = 30/180*pi;
lambda = c/fc;
d = lambda/4;
len = 2048;
t = 0:1/fs:1/fs*(len-1);
st = exp(-1j*2*pi*t*fc);
Phase = 2*pi*d*sin(theta)/lambda;
st = st/trace(st*st');
Interformer01 = st;
%%信道化
D = 16;
si = 1:length(h);
h_channel = zeros(D,length(h));
im = sqrt(-1);
for j = 1:D
h_channel(j,:) = downsample(h.*exp((im*2*pi*((si-1)*(j-1)))/D),1);
end
figure()
for i = 1:D
plot(abs(fft(h_channel(i,:))));
hold on;
end
Interformer_channel = zeros(D,len/D);
for i = 1:D
Interformer_channel(i,:) = downsample(filter(h_channel(i,:),1,Interformer01),D);
end
figure()
for i = 1:D
subplot(4,4,i)
plot(real((Interformer_channel(i,:))));
end
%%信道化实现思路
si_new = 1:length(h)/D;
Interformer01_py = (reshape(Interformer01,D,len/D));
% Interformer01_py = Interformer01_py.*repmat((exp(1j/2*pi*si_new)),length(h)/D,1);
% h_py = reshape(h,D,length(h)/D);
h_py = fliplr(reshape(h,D,length(h)/D));%.*repmat((exp(1j/2*pi*si_new)),D,1);
Interformer02_channel = zeros(D,len/D);
for i = 1:D
Interformer02_channel(i,:) = downsample(filter(h_py(i,:),1,Interformer01_py(i,:)),1);
% Interformer02_channel(i,:) = Interformer02_channel(i,:)*(-1)^(i-1)*exp(-1j*pi/2/D*(i-1));
end
Interformer02_channel = fft(Interformer02_channel);
figure()
for i = 1:D
subplot(4,4,i)
plot(real((Interformer02_channel(i,:))));
end
信道化结果：
直接信道化：
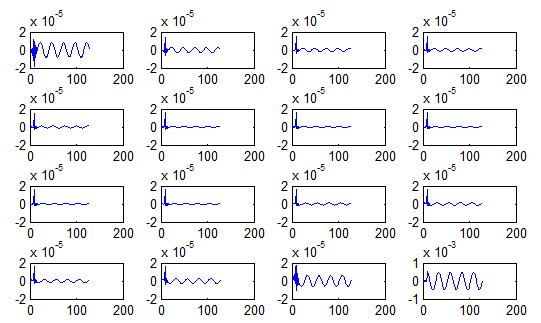
多相实现：
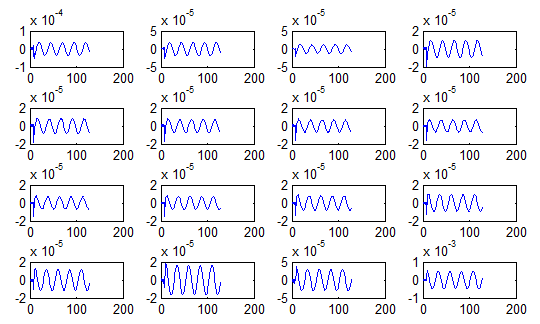
该方式比直接实现，兔耳效应更明显。
