【论文:麦克风阵列增强】Signal Enhancement Using Beamforming and Nonstationarity with Applications to Speech
作者:桂。
时间:2017-06-06 13:25:58
链接:http://www.cnblogs.com/xingshansi/p/6943833.html
论文原文:http://pan.baidu.com/s/1hsuuQYK
前言
上一篇GSC是基于delay的框架进行处理,这是在无混响的情况下一种简单近似处理。许多更为复杂的应用场景,如存在的混响较严重Rt=450ms,则基于delay的模型是不合适的,有学者就考虑直接利用系统的响应函数,也就是传递函数(Transfer function, TF)进行处理,这也就是本文要梳理的思路。
一、理论模型
模型:
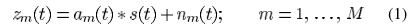
其中

对应的频域变换
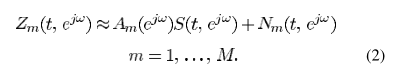
M为麦克风的数量。
问题知道了,剩下就是建模求解。仍然可以是Frost's algorithm和GSC两种框架。与原始问题基本的不同点就是一个:原始的利用delay的延时补偿;此处是基于传递函数TF。用文中的话就是:
In Frost's algorithm, a beamforming algorithm was proposed under the assumption that the TF from the desired signal source to each sensor includes only gain and delay values. In this article, we consider the general case of arbitrary TFs.
二、理论求解
A-Frost's algorithm
滤波器频域系数
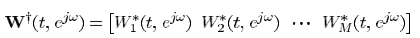
滤波后的信号
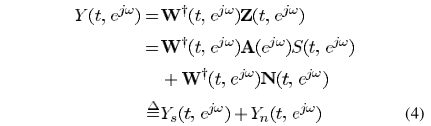
滤波后输出信号的均方值,也就是目标函数:

Frost's algorithm基于MVDR的思路,保证目标信号不失真(限制条件),最小化输出功率(目标函数),这就是一个LCMV(linear constrained minimum variance)问题.约束条件:
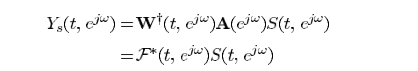
总结一下求解的理论模型

同样的思路,利用拉格朗日乘子法得出滤波器最优解

同之前的问题一样,在实际的工程应用中:
This closed-form solution is difficult to implement and does not have the ability to track changes in the environment. Therefore, an adaptive solution should be more useful.
因此需要借助梯度下降的思路,利用自适应滤波(LMS、NLMS等)进行工程化的落地。
迭代思路

其中
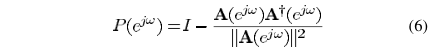
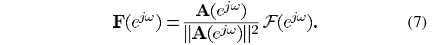
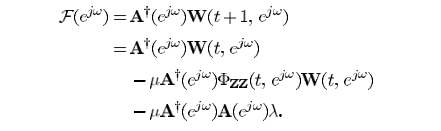
W的迭代也可以进一步简化:
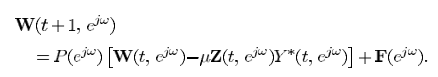 可以看出实现中只要A已知,整个的框架就搭建完成,问题就转换成:A如何求解?GSC框架也存在同样的问题。如果A已知,此处的TF-Frost's algorithm和TF-GSC都可以工程化落地,但实际应用中A通常未知,所以论文也只是交代了思路,只有TF-GSC利用了一种参数转化的思想进行参数估计,实现工程落地,而TF-Frost's algorithm并没有落地,因此论文的实验部分也仅仅是TF-GSC与基于delay的D-GSC对比,提前补充说明一下(个人理解,如果有误还请帮忙指出)。
可以看出实现中只要A已知,整个的框架就搭建完成,问题就转换成:A如何求解?GSC框架也存在同样的问题。如果A已知,此处的TF-Frost's algorithm和TF-GSC都可以工程化落地,但实际应用中A通常未知,所以论文也只是交代了思路,只有TF-GSC利用了一种参数转化的思想进行参数估计,实现工程落地,而TF-Frost's algorithm并没有落地,因此论文的实验部分也仅仅是TF-GSC与基于delay的D-GSC对比,提前补充说明一下(个人理解,如果有误还请帮忙指出)。
回顾一下基于delay的Frost's algorithm框架:

B-TF-GSC
GSC的思想与Frost's algorithm的不同在于,除了利用约束条件
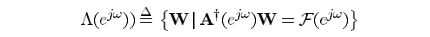
假设矩阵N个自由度,约束条件利用了n个(Frost's algorithm),GSC还利用了剩下的N-n个自由度:
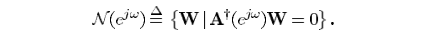
更直观的说,回顾基本GSC框架(本文方法的无t延迟操作)

上支的作用就是Frost's algorithm,下支的Block就是剩下的自由度,所以上支的W与下支的B需要正交,否则冗余。通常为了简便,W与B直接给定,只优化Block之后的参数矩阵,这样一来W就不是最优了,这也是为什么说GSC是Frost's algorithm的扩展不够严谨,如果仅仅从理论框架来讲,GSC就是Frost's algorithm的扩展。
TF-GSC框架的输出
 其中上支是
其中上支是
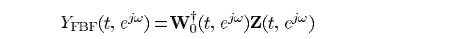 其中
其中
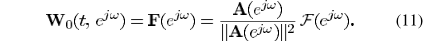
F的定义
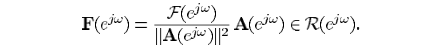
之所以可以W0等于F,是因为
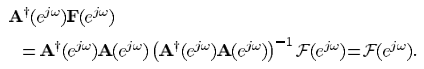
满足向量空间
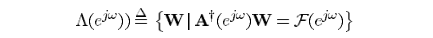
下支是
 因为是利用N-n的自由度,所以
因为是利用N-n的自由度,所以 存在于向量空间
存在于向量空间
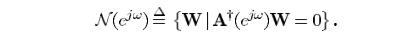
剩下就是自适应滤波求取G了。
进一步讨论之前,再将GSC框架梳理一下(TF-GSC也属于该框架)
1)上支:也就是fixed beamformer,构建带噪的增强信号;例如本文的
2)下支:也就是Blcok matrix,构建噪声参考信号;例如本文的
3)自适应部分:就是针对上支信号,利用下支得到的噪声对其进行自适应处理,例如本文的
处理结束的信号,就是整个GSC框架增强的信号。
说说G的求解过程。
重新写出自适应的准则函数
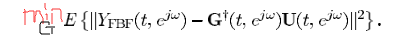
其中
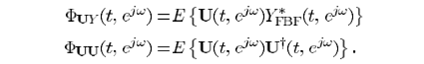
利用最小二乘的思路

考虑到工程的适应性,通常用梯度下降的思想,借助最小二乘实现
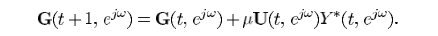
也可以normalized一下,即NLMS
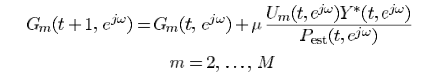
其中Pest的更新方式为
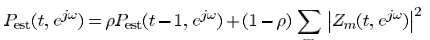
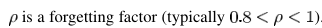
假设G求解完毕,如何工程化实现呢?一种设计思路是借助FIR
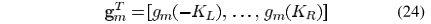
理论上G求解之后,利用最佳逼近,便可得出FIR的设计
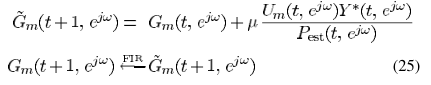
细说就是三步走:1)将估计的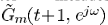 时域变换;2)取时域的区间
时域变换;2)取时域的区间 范围内;3)将处理后的信号变换到频域,认为是利用FIR设计的G,也就是G的最终估计。
范围内;3)将处理后的信号变换到频域,认为是利用FIR设计的G,也就是G的最终估计。
三步走的操作可以让迭代步骤更加Robust.
至此,理论分析已经结束。
C-参数转化
然而直接求解/估计传递函数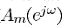 是困难的,这一点很容易理解,但绝对转化为相对,求解就容易了。
是困难的,这一点很容易理解,但绝对转化为相对,求解就容易了。
1-上支
定义
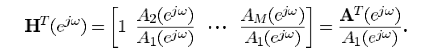
W0重写为
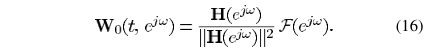
如果H归一化,W0可简写

2-下支
一种构造方式(满足正交空间即可):
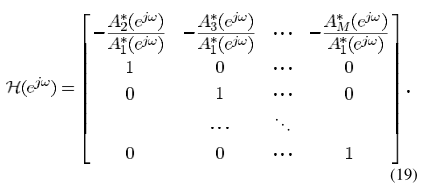
 同样可以由
同样可以由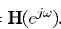 得到。
得到。
3-自适应
这一步按上面的思路工程上完全可以实现。
至此完成了原始问题的参数转化,也就是将绝对求解转化为相对求解,剩下就是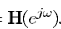 的参数估计了。
的参数估计了。
D-参数估计
考虑到

即

从而
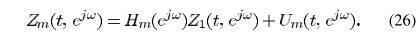
进一步得出

实际操作中,基于平稳遍历的假设,近似估计:

利用K帧数据进行处理
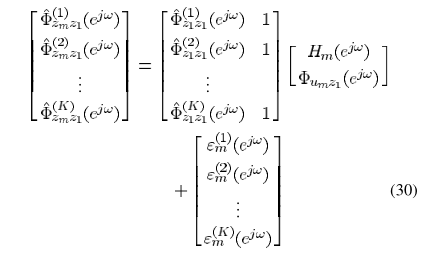
从而实现H的估计:
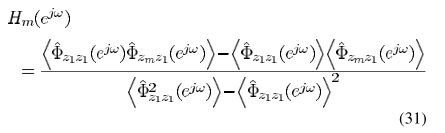
<.>代表均值的操作
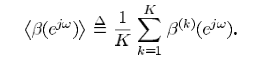
至此TF-GSC完成了理论分析→理论在工程的落地→实际应用的参数估计,反过来看就是整个工程实现的思路搭建完毕。
总结一下算法流程

参考
- Gannot, Sharon, David Burshtein, and Ehud Weinstein. "Signal enhancement using beamforming and nonstationarity with applications to speech." IEEE Transactions on Signal Processing 49.8 (2001): 1614-1626.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号