【论文:麦克风阵列增强】An Algorithm For Linearly Constrained Adaptive Array Processing
作者:桂。
时间:2017-06-03 15:06:37
链接:http://www.cnblogs.com/xingshansi/p/6937635.html
原文链接:http://pan.baidu.com/s/1pKOYuiJ
前言
本文的算法就是在阵列信号增强中非常经典的Frost's Algorithm。上个世纪70年代的技术了,梳理一下该算法的思路。
一、理论框架
首先交代理论模型。噪声为加性噪声:
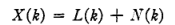
X为带噪信号,L为理想信号,N为噪声信号,目的是希望利用一组滤波器,实现特定信号的增强(Enhancement).
假设有M个麦克风,对应滤波器的抽头系数为J:
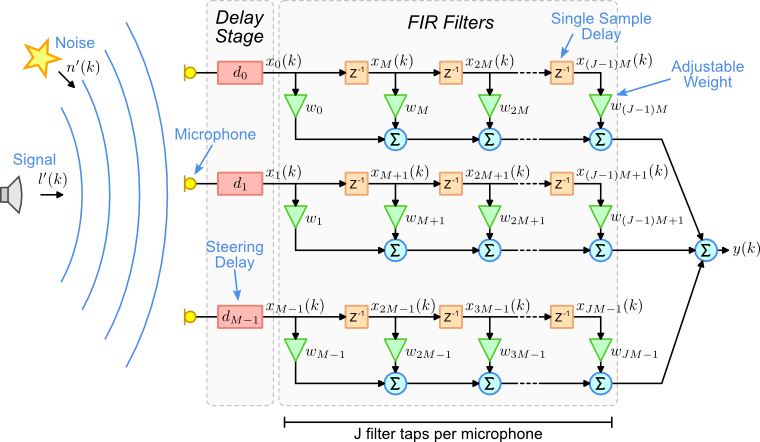
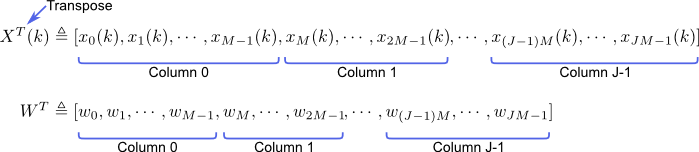
写成向量的形式就是:
MVDR通常是按频点处理,以对第k个频点的处理为例:滤波信号可以表示为

其实框架就是Delay and sum,不同的是权重W不再是均分分布,而是通过最小方差找出最优组合,这就定义了准则函数:

这是一个约束问题,可以借助拉格朗日乘子法求解:
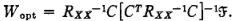
从而得出理想的输出:
例如希望减少noise的时候,原信号保持不变:
这样完成了理论框架的搭建:模型建立→准则函数定义→目标参数求解。
接下来就是落地的问题,即如何将理论模型与实际的工程应用结合起来?
二、实现思路
A-初步实现
首先是Rxx,它应该是一个先验知识priori:
它是随机信号的均值,实际应用中通常是不知道的,我们只有观测信号。因此通常时间换空间,在平稳遍历的基础上用R = 1/T (XXT)来近似表达,这样一来实际的W就可以求解,从而完成了理论的落地。
B-改进思路
这样的R通常是较大的,W的求解涉及到矩阵求逆的问题,运算速度较慢。最优解的求解,一般有最小二乘和梯度下降两个思路。矩阵求逆通常对应最小二乘思路,直接得出最优解,考虑到运算速度,一个直观的思路就是:利用梯度下降的思想。而对于均方意义下的准则函数,梯度是无法求解的,但基于遍历性的假设,可以利用不同时刻的样本进行近似梯度求解,这也就是自适应滤波的思路。梯度下降从样本量的角度来讲,有两个基本思路:随机梯度下降、批量梯度下降,这里以随机梯度下降为例(SGD).梯度下降从下降方式来讲,又有很多分支:一阶梯度下降、二阶梯度下降(Newton-Rapson)等。对于含有约束条件的梯度下降,常用的思路是:投影梯度下降法。文中利用拉格朗日乘子法将含约束的问题转化为无约束问题:
对应的梯度下降:
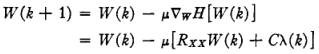
其中λ为:
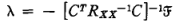
从而梯度下降改写为
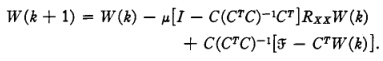
这样一来只有关于C的求逆,这是可以事先求解并固定不变的。定义:
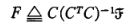
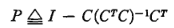
迭代形式简化为

给出完成的梯度下降法思路(初始化+迭代):

至此,速度问题也得以优化,完成了整个MVDR的落地工作。注意到一点:μ作为迭代步长,需要人为给定。给的合适,收敛较好;给的不理想,收敛太慢甚至发散。
C-迭代步长μ的选取
细节不罗列了,需要说明的是分析是基于随机过程的均值。实际LMS应用中的μ并不完全与它吻合。
首先考虑平稳噪声的场景,需要满足:
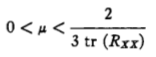
其次考虑非平稳噪声的场景,需要满足:
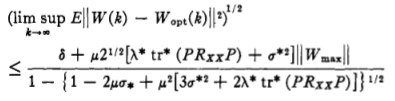
具体推导看原文吧,实际应用中由于场景不同,μ的设定更多的依靠工程经验,这个单靠理论是行不通的。
参考
- Frost, Otis Lamont. "An algorithm for linearly constrained adaptive array processing." Proceedings of the IEEE 60.8 (1972): 926-935.



