矢量量化(VQ)
作者:桂。
时间:2017-05-31 21:14:56
链接:http://www.cnblogs.com/xingshansi/p/6925955.html
前言
VQ(Vector Quantization)是一个常用的压缩技术,本文主要回顾:
1)VQ原理
2)基于VQ的说话人识别(SR,speaker recognition)技术
〇、分类问题
说话人识别其实也是一个分类问题:

说话人识别技术,主要有这几大类方法:
- 模板匹配方法
这类方法比较成熟,主要原理:特征提取、模板训练、匹配。典型的有:动态时间规整DTW,矢量量化VQ等。
DTW利用动态规划的思想,但也有不足:1)过分依赖VAD技术;2)没有充分利用语音的时序动态特性,所以被HMM取代也就容易理解了。
VQ算法是数据压缩的方法。码本简历、码字搜索是两个基本问题,码本简历是从大量信号样本中训练出比较好的码书,码字搜索是找到一个和输入最匹配的码字,该方法简单,对小系统、差别明显的声音较合适。
- 基于统计模型的分类方法
该类方法本质仍是模式识别系统,都需要提取特征,然后训练分类器,最后分类决策,典型框架:
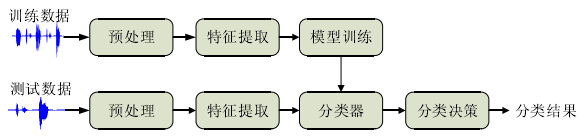
常用的模型有:GMM、HMM、SVM、ANN、DNN或者各种联合模型等。
GMM基本框架:
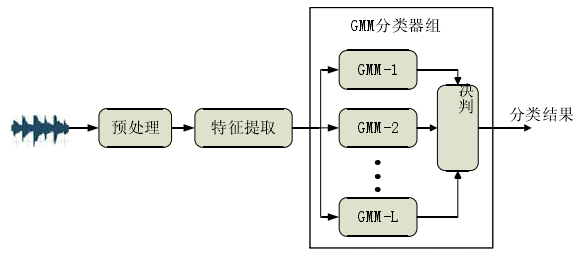
类似的还有GMM-UBM(Universal background model)算法,其与GMM的区别在于:对L类整体样本训练一个大的GMM,而不像GMM对每一类训练一个GMM模型。SVM的话MFCC作为特征,每一帧作为一个样本,可以借助VAD删除无效音频段,直接训练分类。近年来也有利用稀疏表达的方法:

一、VQ原理
此段摘自Pluskid博客。
Vector Quantization 这项技术广泛地用在信号处理以及数据压缩等领域。事实上,在 JPEG 和 MPEG-4 等多媒体压缩格式里都有 VQ 这一步。
Vector Quantization 这个名字听起来有些玄乎,其实它本身并没有这么高深。大家都知道,模拟信号是连续的值,而计算机只能处理离散的数字信号,在将模拟信号转换为数字信号的时候,我们可以用区间内的某一个值去代替着一个区间,比如,[0, 1) 上的所有值变为 0 ,[1, 2) 上的所有值变成 1 ,如此类推。其这就是一个 VQ 的过程。一个比较正式一点的定义是:VQ 是将一个向量空间中的点用其中的一个有限子集来进行编码的过程。
一个典型的例子就是图像的编码。最简单的情况,考虑一个灰度图片,0 为黑色,1 为白色,每个像素的值为 [0, 1] 上的一个实数。现在要把它编码为 256 阶的灰阶图片,一个最简单的做法就是将每一个像素值 x 映射为一个整数 floor(x*255) 。当然,原始的数据空间也并不以一定要是连续的。比如,你现在想要把压缩这个图片,每个像素只使用 4 bit (而不是原来的 8 bit)来存储,因此,要将原来的 [0, 255] 区间上的整数值用 [0, 15] 上的整数值来进行编码,一个简单的映射方案是 x*15/255 。
不过这样的映射方案颇有些 Naive ,虽然能减少颜色数量起到压缩的效果,但是如果原来的颜色并不是均匀分布的,那么的出来的图片质量可能并不是很好。例如,如果一个 256 阶灰阶图片完全由 0 和 13 两种颜色组成,那么通过上面的映射就会得到一个全黑的图片,因为两个颜色全都被映射到 0 了。一个更好的做法是结合聚类来选取代表性的点。
实际做法就是:将每个像素点当作一个数据,跑一下 K-means ,得到 k 个 centroids ,然后用这些 centroids 的像素值来代替对应的 cluster 里的所有点的像素值。对于彩色图片来说,也可以用同样的方法来做,例如 RGB 三色的图片,每一个像素被当作是一个 3 维向量空间中的点。
用本文开头那张 Rechard Stallman 大神的照片来做一下实验好了,VQ 2、VQ 10 和 VQ 100 三张图片分别显示聚类数目为 2 、10 和 100 时得到的结果:

传统LBG算法就是K-means,基于分裂的LBG称为LBG-VQ,LBG-VQ算法以及K-means:
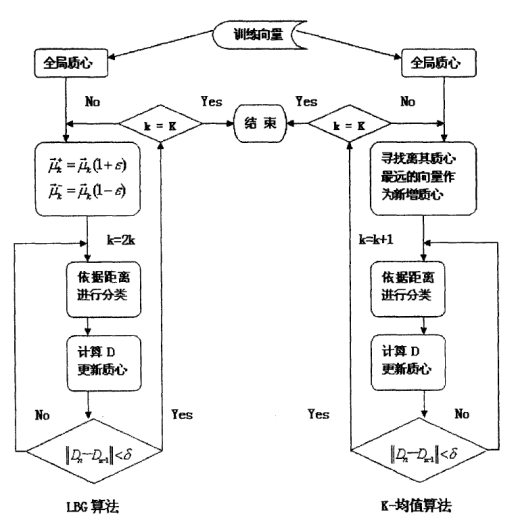
二、基于VQ的说话人识别技术
基于VQ方法:例如N个说话人,每个说话人建立一个码本,共N个码本。每个码本如何建立呢?以MFCC为例,M帧的MFCC,每一帧都是一个多维N的样本点,训练数据量通常较大MxN,聚类成K类是容易实现的(K<<M),LBG-VQ的思路则是利用分裂的思想,通常按倍数递增,知道码本数量增加到:码本的误差达到预设值停止,最终的结果相当于降维:KxN,也就是码本的维度。
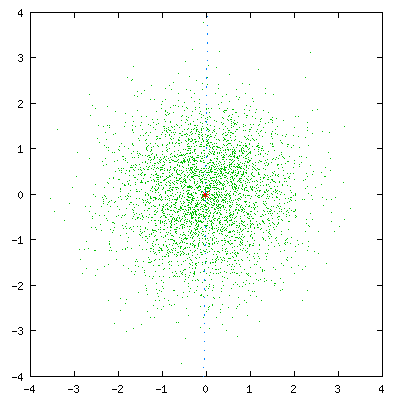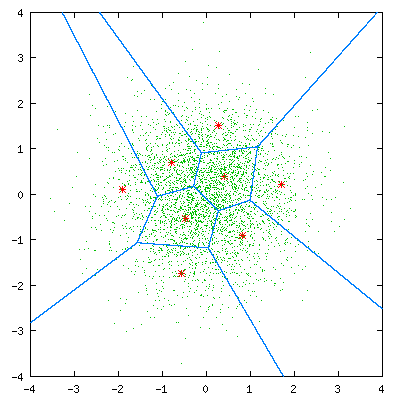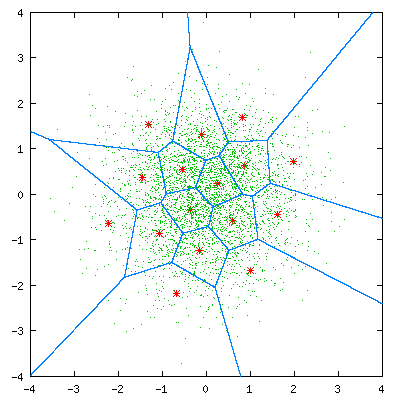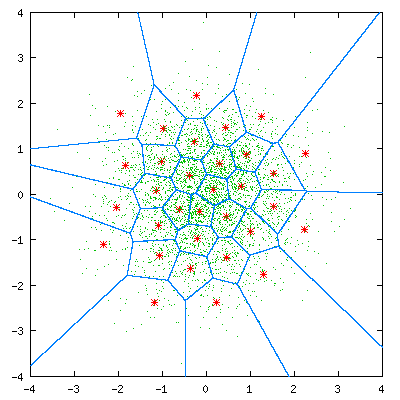
总结一下基于VQ的说话人识别的基本思路:
1)训练:分别针对每个说话人提取特征,利用特征训练码本(Kmeans/LBG-VQ等方法);
2)识别:提取测试数据的特征,与码本匹配,误差距离归一化并求和,最小值即为对应的说话人;
VQLBG代码:
%% VQLBG Vector quantization using the Linde-Buzo-Gray algorithm
% VQLBG Vector quantization using the Linde-Buzo-Gray algorithm
%
% Inputs: d contains training data vectors (one per column)
% k is number of centroids required
%
% Output: r contains the result VQ codebook (k columns, one for each centroids)
function r = vqlbg(d,k)
e = .01;
r = mean(d, 2);
dpr = 10000;
for i = 1:log2(k)
r = [r*(1+e), r*(1-e)];
while (1 == 1)
z = disteu(d, r);
[m,ind] = min(z, [], 2);
t = 0;
for j = 1:2^i
r(:, j) = mean(d(:, find(ind == j)), 2); %#ok<FNDSB>
x = disteu(d(:, find(ind == j)), r(:, j)); %#ok<FNDSB>
for q = 1:length(x)
t = t + x(q);
end
end
if (((dpr - t)/t) < e)
break;
else
dpr = t;
end
end
end
end
%% DISTEU Function
% DISTEU Pairwise Euclidean distances between columns of two matrices
%
% Input:
% x, y: Two matrices whose each column is an a vector data.
%
% Output:
% d: Element d(i,j) will be the Euclidean distance between two
% column vectors X(:,i) and Y(:,j)
%
% Note:
% The Euclidean distance D between two vectors X and Y is:
% D = sum((x-y).^2).^0.5
function d = disteu(x, y)
[M, N] = size(x);
[M2, P] = size(y);
if (M ~= M2)
error('Matrix dimensions do not match.')
end
d = zeros(N, P);
% if (N < P)
% copies = zeros(1,P);
% for n = 1:N
% d(n,:) = sum((x(:, n+copies) - y) .^2, 1);
% end
% else
% copies = zeros(1,N);
% for p = 1:P
% d(:,p) = sum((x - y(:, p+copies)) .^2, 1)';
% end
% end
% d = d.^0.5;
for ii=1:N
for jj=1:P
%d(ii,jj)=sum((x(:,ii)-y(:,jj)).^2).^0.5;
d(ii,jj) = mydistance(x(:,ii),y(:,jj),2);
end
end
%--------------------------------------------------------------------------
%--------------------------------------------------------------------------
end
识别的主要code:
v = mfcc(str{classe},fstr{classe});
% Current distance and sound ID initialization
distmin = Inf;
k1 = 0;
for ii=1:sound_number
d = disteu(v, code{ii});
dist = sum(min(d,[],2)) / size(d,1);
if dist < distmin
distmin = dist;
k1 = ii;
end
end
min_index = k1;
参考
- http://blog.pluskid.org/?p=57
- http://blog.csdn.net/momosp/article/details/7626971


