谱聚类(Spectral clustering)(2):NCut
作者:桂。
时间:2017-04-13 21:19:41
链接:http://www.cnblogs.com/xingshansi/p/6706400.html
声明:欢迎被转载,不过记得注明出处哦~

前言
本文为谱聚类的第二篇,主要梳理NCut算法,关于谱聚类的更多细节信息,可以参考之前的博文:
1)拉普拉斯矩阵(Laplace Matrix)与瑞利熵(Rayleigh quotient)
内容主要参考刘建平Pinard博客,更多细节可以参考该作者博文,本文最后给出代码实现,全文包括:
1)NCut原理
2)NCut算法实现
一、NCut原理
Ncut切图和RatioCut切图很类似,但是把Ratiocut的分母$|Ai|$换成$vol(A_i)$,由于子图样本的个数多并不一定权重就大,我们切图时基于权重也更合我们的目标,因此一般来说Ncut切图优于RatioCut切图。
$vol(A): = \sum\limits_{i \in A}d_i$

对应的,Ncut切图对指示向量h做了改进。注意到RatioCut切图的指示向量使用的是$\frac{1}{\sqrt{|A_j|}}$标示样本归属,而Ncut切图使用了子图权重$\frac{1}{\sqrt{vol(A_j)}}$来标示指示向量h,定义如下:
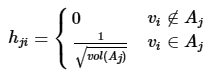
那么我们对于$h_i^TLh_i$有:
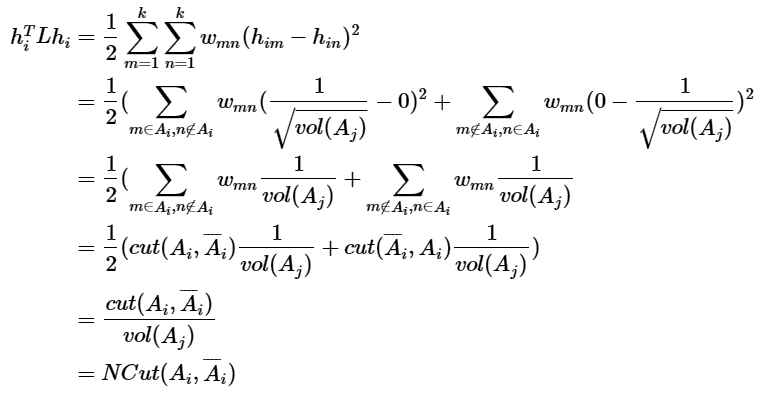
推导方式和RatioCut完全一致。也就是说,我们的优化目标仍然是

但是此时我们的$H^TH \neq I$而是$H^TDH = I$,推导如下:
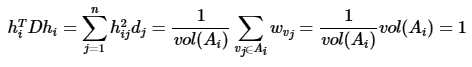
也就是说,此时我们的优化目标最终为:

这个就是泛化瑞利熵的求解问题,之前文章分析过。这里再次给出细节分析。
令$H = D^{-1/2}F$,则优化目标转化为:

至此已经完成了NCut的理论。
画蛇添足一下吧,注意到:
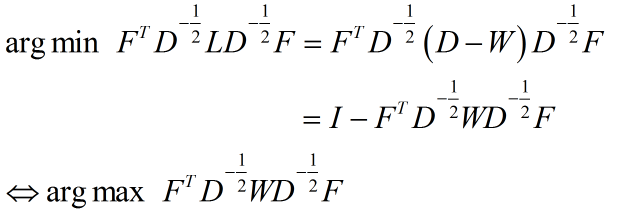
事实上,连拉普拉斯矩阵都懒得构造了。
二、NCut算法实现
首先给出算法步骤:
步骤一:求解邻接矩阵W和度矩阵D
步骤二:对${D^{ - \frac{1}{2}}}W{D^{ - \frac{1}{2}}}$进行特征值分解,并取K个最大特征值对应的特征向量(K为类别数目)
步骤三:将求解的K个特征向量(并分别归一化),构成新的矩阵,对该矩阵进行Kmeans处理
Kmeans得到的类别标签,就是原数据的类别标签,至此完成NCut聚类。
给出代码实现:
sigma2 = 0.01;
%%Step1: Calculate matrixs
for i = 1:N
for j =1:N
W(i,j) = exp(-sqrt(sum((X(i,:)-X(j,:)).^2))/2/sigma2);
end
end
W = W-diag(diag(W));% adjacency matrix
D = diag(sum(W)); %degree matrix
%%Step2:Eigenvalues decomposition
K = 3;
[Q,V] = eigs(D^(-1/2)*W*D^(-1/2),K);
%%Step3:New matrix Q
Q = Q./repmat(sqrt(diag(Q'*Q)'),N,1);
[idx,ctrs] = kmeans(Q,K);
结果图:
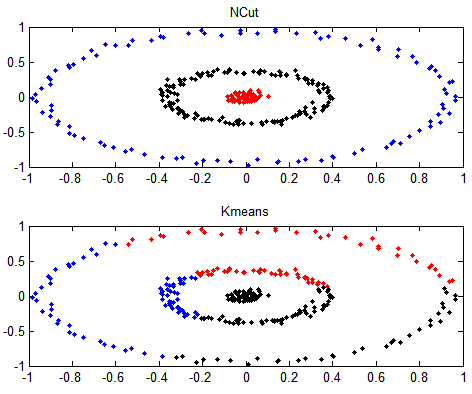
测试一下,按数据为3类进行谱聚类,可以看出来还是有效的,谱聚类中高斯权重涉及到$\sigma$如何取值,不过这里就不做进一步讨论了。
参考:


