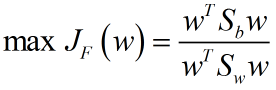拉普拉斯矩阵(Laplace Matrix)与瑞利熵(Rayleigh quotient)
作者:桂。
时间:2017-04-13 07:43:03
链接:http://www.cnblogs.com/xingshansi/p/6702188.html
声明:欢迎被转载,不过记得注明出处哦~

前言
前面分析了非负矩阵分解(NMF)的应用,总觉得NMF与谱聚类(Spectral clustering)的思想很相似,打算分析对比一下。谱聚类更像是基于图(Graph)的思想,其中涉及到一个重要概念就是拉普拉斯矩阵(Laplace matrix),想着先梳理一下这个矩阵:
1)拉普拉斯矩阵基本定义
2)拉普拉斯矩阵意义及性质
3)瑞利熵(Rayleigh quotient)
内容为自己的学习记录,很多地方都借鉴了别人,最后一并给出链接。
一、拉普拉斯矩阵基本定义
对于图G,一般用点的集合V和边的集合E来描述:G(V,E)。现在有这样一个图,如何定义拉普拉斯矩阵呢?这里涉及到两个常用矩阵:邻接矩阵、度矩阵。
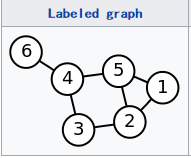
从最简单的应用入手,不同数据点相通权重为1,不相通权重为0.
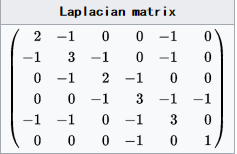
首先求解邻接矩阵W:

将每一列求和,这个数值的对角形式对应就是度矩阵D:
$d_i = \sum\limits_{j=1}^{n}w_{ij}$
写成矩阵形式:
$\mathbf{D} = \left( \begin{array}{ccc} d_1 & \ldots & \ldots \\ \ldots & d_2 & \ldots \\ \vdots & \vdots & \ddots \\ \ldots & \ldots & d_n \end{array} \right)$

从而得到拉普拉斯矩阵L的定义:
$L= D-W$
二、拉普拉斯矩阵意义及性质
不失一般性,$v_i$与$v_j$的权重不再是1而是$w_{ij}$,$f(v_i)$表示节点$v_i$的函数,对应实际应用它可以是一个概率值、一个像素值等等。
对任意向量$f$,
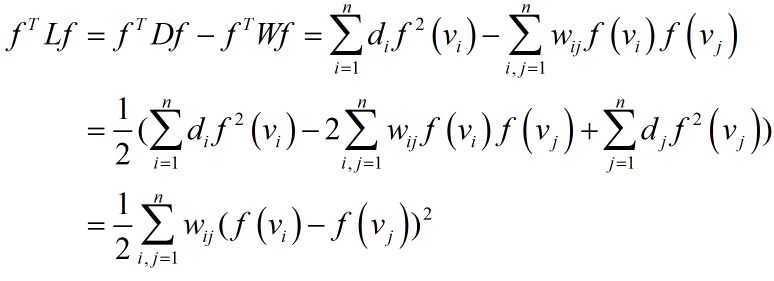
这样一来,拉普拉斯矩阵的意义就比较明显了,它是一种基于欧式距离的测度,如果$w_{ij} = 1$,上式对应就是多有数据点的距离之和,同时也可以看出:D对应二次项,W对应不同一次项相乘。拉普拉斯矩阵是半正定的,且对应的n个实数特征值都大于等于0,即:$0 =\lambda_1 \leq \lambda_2 \leq... \leq \lambda_n$。
三、瑞利熵
提到拉普拉斯矩阵,就不能不提瑞利熵。
A-普通瑞利熵
给出定义:
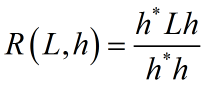
因为对h幅值进行条件,不会影响R的取值,同时也不会改变h向量的方向,对于一般优化问题(以max为例,其他类似):
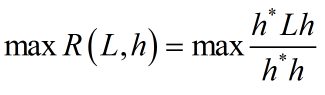
可以转化为拉格朗日乘子问题:

c为常数,即:
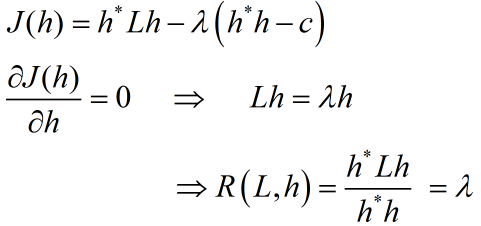
可以看出:
- R的最大值就是L最大特征值,R的最小值就是L最小特征值
- h的解,就是L对应的特征向量
是不是很熟悉啊?
- 简单回顾一下主成分分析(PCA)算法:
设p为矩阵A的单位投影矩阵,最大化投影结果:
PCA就是瑞利熵理论的一个应用。
后面分析谱聚类(Spectral clustering),其中RatioCut算法也是瑞利熵的一个应用。
B-泛化瑞利熵
为什么叫泛化呢?对于
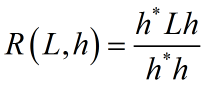
可以看到分子是一般形式,而分母是${{h^*}Dh}$在D取单位阵时的特殊情况,将其一般化:
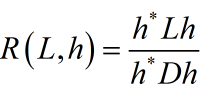
同理可以得到:

适当变形:
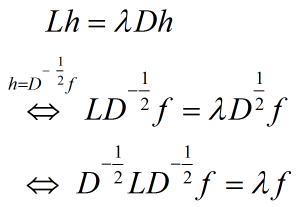
这个时候表达式就是:
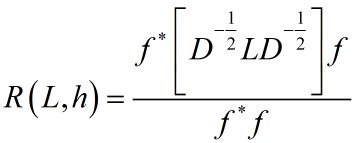
又回到了普通瑞利熵问题,求解就方便了。
- 简单回顾一下Fisher线性判别分析(Linear discriminant analysis, LDA)算法:
Fisher判别准则函数:
分子分母分别是类内、类间距离。这个准则函数就是泛化瑞利熵的形式。
LDA是泛化瑞利熵的一个应用。
后面分析谱聚类(Spectral clustering),其中NCut算法也是泛化瑞利熵的一个应用。
参考: