非负矩阵分解(3):拉格朗日乘子法求解
作者:桂。
时间:2017-04-07 07:11:54
链接:http://www.cnblogs.com/xingshansi/p/6679325.html
声明:欢迎被转载,不过记得注明出处哦~

前言
本文为非负矩阵分解系列第三篇,在第二篇中介绍了不同准则下乘法算法的推导及代码实现,这里不免有一个疑问:明明是一个约束的优化问题,虽然乘法算法巧妙地将其变为一个无约束优化问题,梯度下降到乘法算法的转化,既让人觉得奇妙,又有点莫名其妙。不失一般性,约束问题应该是可以利用拉格朗日乘子法求解,本文打算对此进行梳理,内容主要包括:
1)无约束求解NMF;
2)拉格朗日乘子法求解NMF;
内容为自己的心得体会,许多问题自己也不是很有把握,其中错误的地方希望各位帮忙指出来,全文多有借鉴他人之处,最后一并给出链接。
一、无约束求解NMF
本文主要以Euclidean距离为例,KL散度等不同准则都是大同小异的,就不一一啰嗦了。
考虑无约束优化问题:
![]()
利用梯度下降:
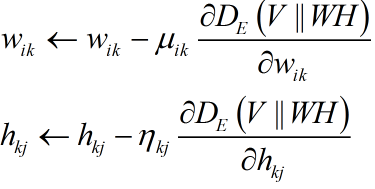
其中:
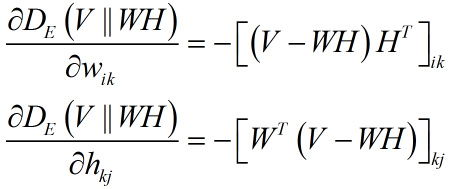
如果直接梯度下降,对于无约束的优化问题,我们不能保证结果都是非负的,下面巧妙之处来了:将梯度下降法变为乘法算法。
令:
梯度下降法变换为乘法算法:
真是巧妙!一个复杂的约束性优化问题,就让一个简单的无约束给解决了。这样一来,如果原矩阵为非负,W、H初始值同样非负,结果自始至终都是非负,直至迭代到满足收敛条件。
收敛性证明可以参考:Lee D D, Seung H S. Algorithms for Non-negative Matrix Factorization[C]// NIPS. 2000:556--562.
对应代码以及更多理论细节,可以参考NMF的上一篇文章。
二、拉格朗日乘子法求解NMF
看到上面的乘法算法,难免感叹它的奇妙,但其实中规中矩,也自有一番力量。对于含有约束的优化问题,这里就采用通用的方法——拉格朗日乘子法。关于拉格朗日乘子法,更多细节可以参考之前的一篇博文。
A-KKT条件
给出约束优化原始问题模型:

其中${h_i}\left( x \right) = 0,\;i = 1,...q$也可写成矩阵形式:${\bf{Ax}} = {\bf{b}}$.该模型为原始问题。
该模型利用拉格朗日乘子可以松弛为无约束优化问题:
$\min \;\;L\left( {x,\lambda ,v} \right) = {f_0}\left( x \right) + \sum\limits_{i = 1}^m {{\lambda _i}{f_i}\left( x \right) + \sum\limits_{i = 1}^q {{v_i}{h_i}\left( x \right)} } $
该模型为对偶问题。(不是对偶方法哦,仅仅是对偶问题,不要搞混了,对偶方法中采用minmax、maxmin之类的问题)
将有约束的原始问题转化为无约束的对偶问题,局部极小解的一阶必要条件(即Karush-Kurth-Tucker,KKT)为:

为什么有这几个约束?更多细节问题同样参考之前的一篇博文,这里就不再多说了。
B-拉格朗日乘子求解NMF
考虑有约束优化问题:
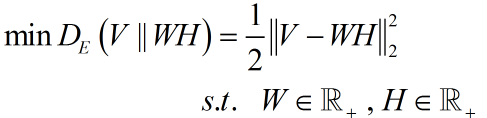
将有约束的原始问题转化为无约束的对偶问题(因为是非负,故约束前添加负号):
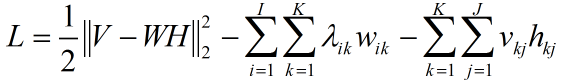
利用梯度下降求解(W、H为复数的情况不考虑):
其中:
将梯度下降的结果变形为:
利用KKT条件,上式就是:
这个式子求解出的W和H,就是局部最优解。虽然是两个式子,两个未知数,看似直接求解,其实不行。这里有个问题:知道W可以解出H,知道H可以解出W,又是一个鸡生蛋蛋生鸡的问题。是不是很熟悉?在分析EM的时候,就是这个问题,所有才有E(expectation)、M(maximize)问题。不过这里用不到EM,因为EM算法的核心是Q函数,而不是两步走问题,任何最大似然估计,参数互相渗透,都有两步走问题呀,这类问题分析过,详细可以参考之前的文章,这里只说说两步走。
参数如何求解呢?接着思路往下走。
C-参数求解
说是两步走,其实就是这么个思路:
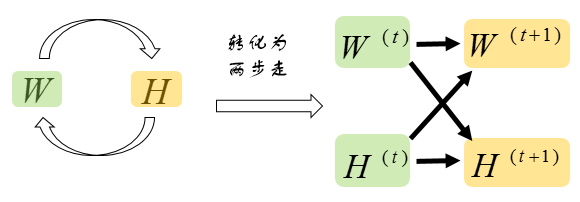
将纠缠不清的问题,转化为:按迭代次序依次推进。这跟之前EM算法一文中的硬币第三抛问题很像,对应的解法就是那篇文中说的山寨版EM算法。给出结果:
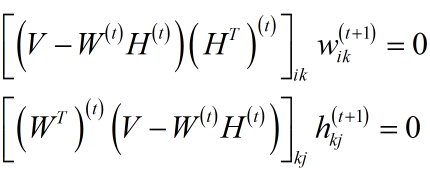
有时为了简便,将迭代次数(t)、(t+1)略去:
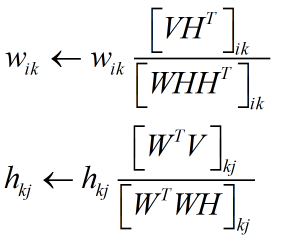
这不就是乘法算法?至于收敛性,证明与之前一致就可以了。还是拉格朗日乘子法比较直观,用着按部就班就能得出结果来。

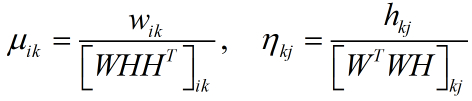

 浙公网安备 33010602011771号
浙公网安备 33010602011771号