非负矩阵分解(2):算法推导与实现
作者:桂。
时间:2017-04-06 20:26:01
链接:http://www.cnblogs.com/xingshansi/p/6670214.html
声明:欢迎被转载,不过记得注明出处哦~

前言
本文非负矩阵分解(Nonegative matrix factorization,NMF)系列第二篇,主要介绍最基本的NMF原理及代码实现,内容主要包括:
1)基于Euclidean距离的NMF推导及实现;
2)基于KL散度的NMF推导及实现;
3)NMF应用示例
开始之前,有两点需要补充:
- 前面分析用的是X=AS形式,感觉别扭,好多文章都是用V = WH,后续打算也采用这也表达方式;
- NMF其实是含有约束的优化问题,但乘法算法可以巧妙得让我们只需讨论:无约束优化问题。
一、基于Euclidean距离的NMF推导及实现
考虑无约束优化问题:
![]()
利用梯度下降:
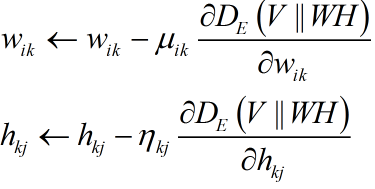
其中:
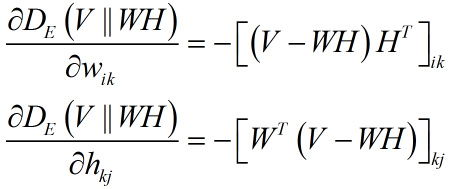
如果直接梯度下降,对于无约束的优化问题,我们不能保证结果都是非负的,下面巧妙之处来了:将梯度下降法变为乘法算法。
令:
梯度下降法变换为乘法算法:
真是巧妙!一个复杂的约束性优化问题,就让一个简单的无约束给解决了。这样一来,如果原矩阵为非负,W、H初始值同样非负,结果自始至终都是非负,直至迭代到满足收敛条件。
收敛性证明可以参考:Lee D D, Seung H S. Algorithms for Non-negative Matrix Factorization[C]// NIPS. 2000:556--562.
给出对应的代码实现:
function [W, H] = nmf(V, K, MAXITER)
%Euclidean distance
F = size(V,1);
T = size(V,2);
rand('seed',0)
W = 1+rand(F, K);
% W = W./repmat(sum(W),F,1);
H = 1+rand(K, T);
ONES = ones(F,T);
for i=1:MAXITER
H = H .* (W'*V)./(W'*W*H+eps) ;
W = W .* (V*H')./(W*H*H'+eps);
end
其实关键的就是循环里的两行。
二、基于KL散度的NMF推导及实现
整个思路与Euclidean distance下的求解思路如出一辙。
考虑无约束优化问题:

利用梯度下降算法:

其中:

根据梯度下降算法转化为乘法算法:
令:
梯度下降算法改写为乘法算法:
收敛性证明可以参考:Lee D D, Seung H S. Algorithms for Non-negative Matrix Factorization[C]// NIPS. 2000:556--562.
对应代码:
function [W, H] = nmf(V, K, MAXITER)
%KL-divergence
F = size(V,1);
T = size(V,2);
rand('seed',0)
W = 1+rand(F, K);
% W = W./repmat(sum(W),F,1);
H = 1+rand(K, T);
ONES = ones(F,T);
for i=1:MAXITER
H = H .* (W'*( V./(W*H+eps))) ./ (W'*ONES);
W = W .* ((V./(W*H+eps))*H') ./(ONES*H');
end
三、NMF应用示例
对于一个混合语音,如鼓点和管乐器混合的单通道声音,可以利用非负矩阵进行分解,实现语音信号的分离。
思路:
语音的时频分析,得到的语谱图是一个二维数据矩阵,其中鼓点、管乐器的概率分布不同,利用NMF可以实现信号的分离。
对应代码(NMF调用上面任何一个都可以):
% Read in audio file
[x0 fs] = audioread('test_audio.wav');
x = x0(1:5*fs);%read 5s wav
nw = 1024;
ni = 256;
X = fft(enframe(x,nw,ni)');
V = abs(X);
% NMF
K = 2; % number of basis vectors
MAXITER = 200; % total number of iterations to run
[W, H] = nmf(V, K, MAXITER);
% get the mixture phase
phi = angle(X);
%Reconstruct
X1 = W(:,1)*H(1,:);
X2 = W(:,2)*H(2,:);
s1 = zeros(1,length(x));
s2 = zeros(1,length(x));
for i = 1:size(X1,2)
nic = (1+(i-1)*ni):(nw+(i-1)*ni);
s1(1,nic) = s1(1,nic)+real(ifft(X1(:,i).*exp(1j*phi(:,i))))';
s2(1,nic) = s2(1,nic)+real(ifft(X2(:,i).*exp(1j*phi(:,i))))';
end
s1 = s1/max(abs(s1));
s2 = s2/max(abs(s2));
可以看出这里K是给定的,即NMF实现分解需要给出先验的类别数。这里给出语谱图,图片可以更加直观地观察分离效果,结果图:

看看时域的分离效果:

分离效果还是不错的。
参考:
- Lee D D, Seung H S. Algorithms for Non-negative Matrix Factorization[C]// NIPS. 2000:556--562.
- 张贤达:《矩阵分析与应用,第二版》.