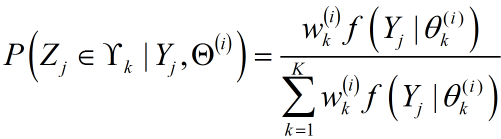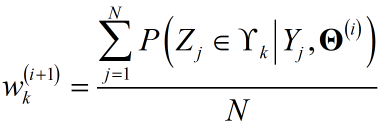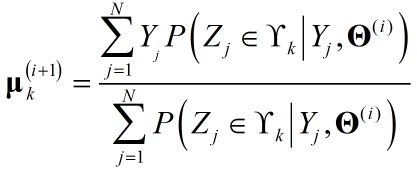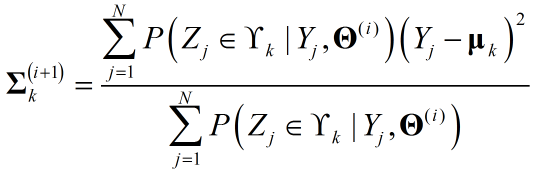混合高斯模型(GMM)推导及实现
作者:桂。
时间:2017-03-20 06:20:54
链接:http://www.cnblogs.com/xingshansi/p/6584555.html

前言
本文是曲线拟合与分布拟合系列的一部分,主要总结混合高斯模型(Gaussian Mixture Model,GMM),GMM主要基于EM算法(前文已经推导),本文主要包括:
1)GMM背景介绍;
2)GMM理论推导;
3)GMM代码实现;
内容多有借鉴他人,最后一并给出链接。
一、GMM背景
A-高斯模型1
给出单个随机信号(均值为-2,方差为9的高斯分布),可以利用最大似然估计(MLE)求解分布参数:

B-高斯模型2
对于单个高斯模型2(均值为3,方差为1),同样可以利用MLE求解:
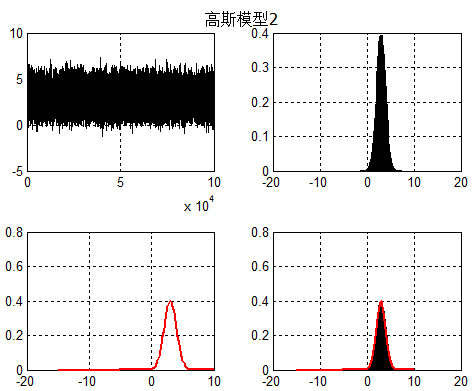
C-高斯模型3
现在对于一个随机数,每一个点来自混合模型1概率为0.5,来自混合模型2概率为0.5,得到统计信息:
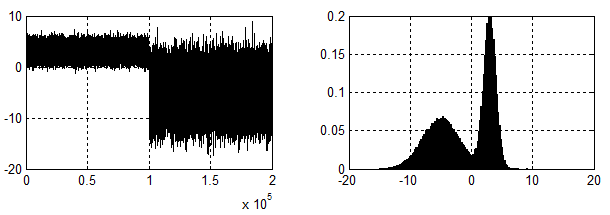
可能已经观察到:只要将信号分为前后两段分别用MLE解高斯模型不就可以?其实这个时候,已经默默地用了一个性质:数据来自模型1或2的概率为0.5,可见一旦该特性确定,混合模型不过是普通的MLE求解问题,可现实情况怎么会这么规律呢,数据来自模型1或2的概率很难通过观察得出。观测数据$Y_1$来自模型1,$Y_2$来自模型2...参差交错。
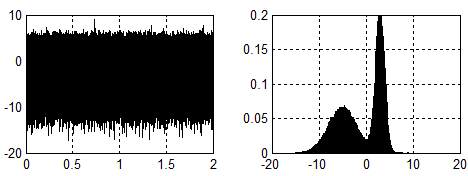
再分两段看看?如果直接利用MLE求解,这就碰到了与之前分析EM时:硬币第三抛同样的尴尬。先看一下EM解决的效果:
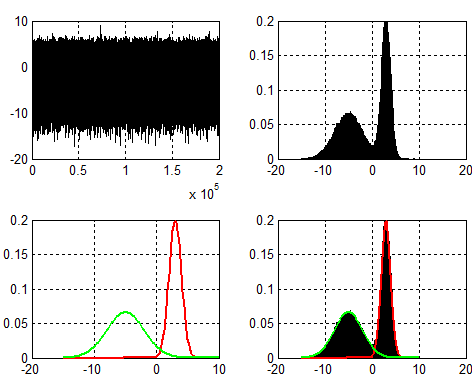
其实硬币第三抛,也是一个混合概率模型:对于任意一个观测点以概率$\pi$选择硬币A,以概率$1-\pi$选择硬币B,对应混合模型为:
$P\left( {{Y_j}|\theta } \right) = {w_1}{P_A} + {w_2}{P_B} = \pi {P_A} + \left( {1 - \pi } \right){P_B}$
同样,对于两个高斯的混合模型(连续分布,故不用分布率,而是概率密度):
![]()
推而广之,对于K个高斯的混合模型:

二、GMM理论推导
可以看出GMM与抛硬币完全属于一类问题,故采用EM算法求解,按模式识别(2)——EM算法的思路进行求解。
记:观测数据为$Y$={$Y_1,Y_2,...Y_N$},对应隐变量为$Z$={$Z_1,Z_2,...Z_N$}。
写出EM算法中Q函数的表达式:
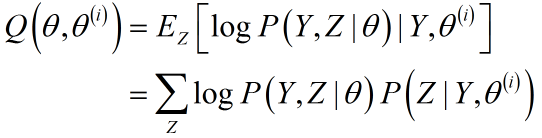
E-Step:
1)将缺失数据,转化为完全数据
主要求解:$P\left( {{Z_j}|{Y_j},{\Theta ^{\left( i \right)}}} \right)$,此处的求解与EM算法一文中硬币第三抛的思路一致,只要求出$P\left( {{Z_j} \in {\Upsilon _k}|{Y_j},{\Theta ^{\left( i \right)}}} \right)$即可,${{Z_j} \in {\Upsilon _k}}$表示第$j$个观测点来自第$k$个分模型。同硬币第三抛的求解完全一致,利用全概率公式,容易得到:
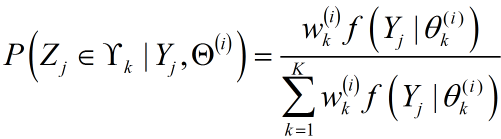
为了推导简洁,M-Step时保留隐变量概率的原形式而不再展开。
2)构造准则函数Q
根据上面给出的Q,可以写出混合分布模型下的准则函数:
$Q\left( {\Theta ,{\Theta ^{\left( i \right)}}} \right) = \sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {\log \left( {{w_k}} \right)P\left( {{Z_j} \in {\Upsilon _k}|{Y_j},{\Theta ^{\left( i \right)}}} \right)} } + \sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {\log \left( {{f_k}\left( {{Y_j}|{Z_j} \in {\Upsilon _k},{\theta _k}} \right)} \right)} } P\left( {{Z_j} \in {\Upsilon _k}|{Y_j},{\Theta ^{\left( i \right)}}} \right)$
其中${{\theta _k}} = [\mu_k,\sigma_k]$为分布$k$对应的参数,$\Theta$ = {$\theta _1$,$\theta _2$,...,$\theta _K$}为参数集合,$N$为样本个数,$K$为混合模型个数。
得到$Q$之后,即可针对完全数据进行MLE求参,可以看到每一个分布的概率(即权重w)与该分布的参数在求参时,可分别求解。由于表达式为一般形式,故该性质对所有混合分布模型都适用。所以对于混合模型,套用Q并代入分布具体表达式即可。
M-Step:
1)MLE求参
- 首先对${{w_k}}$进行优化
由于$\sum\limits_{k = 1}^M {{w_k}} = 1$,利用Lagrange乘子求解:
${J_w} = \sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {\left[ {\log \left( {{w_k}} \right)P\left( {\left. {{Z_j} \in {\Upsilon _k}} \right|{Y_j},{{\bf{\Theta }}^{\left( i \right)}}} \right)} \right]} } + \lambda \left[ {\sum\limits_{k = 1}^K {{w_k}} - 1} \right]$
求偏导:
$\frac{{\partial {J_w}}}{{\partial {w_k}}} = \sum\limits_{J = 1}^N {\left[ {\frac{1}{{{w_k}}}P\left( {{Z_j} \in {\Upsilon _k}|{Y_j},{{\bf{\Theta }}^{\left( i \right)}}} \right)} \right] + } \lambda = 0$
得
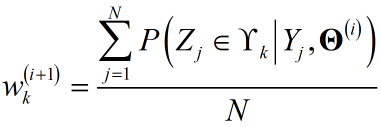
- 对各分布内部参数$\theta_k$进行优化
给出准则函数:
${J_\Theta } = \sum\limits_{j = 1}^N {\sum\limits_{k = 1}^K {\log \left( {{f_k}\left( {{Y_j}|{Z_j} \in {\Upsilon _k},{\theta _k}} \right)} \right)} } P\left( {{Z_j} \in {\Upsilon _k}|{Y_j},{\Theta ^{\left( i \right)}}} \right)$
高维数据,$Y_j$为向量或矩阵,对于高斯分布:
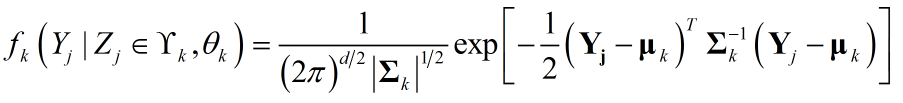
关于$\theta_k$利用MLE即可求参,注意对${{{\bf{\Sigma }}_k}}$求偏导时,关于${{{\bf{\Sigma }}^{-1}_k}}$求偏导更方便,得出结果:
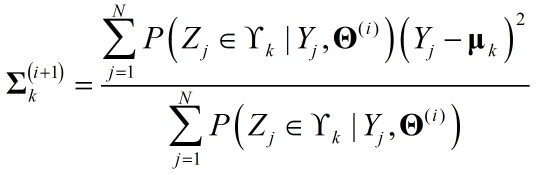
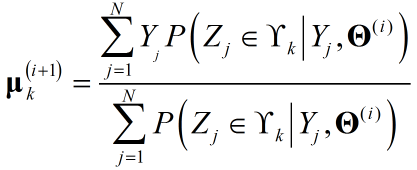
至此,完成了参数求导,可见推导前半部分对于任意分布都有效。只是涉及具体求参时,形式不同有差别。
总结一下GMM:
E-Step:
M-Step:
三、GMM代码实现
子程序代码:
function [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% fit_mix_gaussian - fit parameters for a mixed-gaussian distribution using EM algorithm
%
% format: [u,sig,t,iter] = fit_mix_gaussian( X,M )
%
% input: X - input samples, Nx1 vector
% M - number of gaussians which are assumed to compose the distribution
%
% output: u - fitted mean for each gaussian
% sig - fitted standard deviation for each gaussian
% t - probability of each gaussian in the complete distribution
% iter- number of iterations done by the function
%
% initialize and initial guesses
N = length( X );
Z = ones(N,M) * 1/M; % indicators vector
P = zeros(N,M); % probabilities vector for each sample and each model
t = ones(1,M) * 1/M; % distribution of the gaussian models in the samples
u = linspace(min(X),max(X),M); % mean vector
sig2 = ones(1,M) * var(X) / sqrt(M); % variance vector
C = 1/sqrt(2*pi); % just a constant
Ic = ones(N,1); % - enable a row replication by the * operator
Ir = ones(1,M); % - enable a column replication by the * operator
Q = zeros(N,M); % user variable to determine when we have converged to a steady solution
thresh = 1e-3;
step = N;
last_step = inf;
iter = 0;
min_iter = 10;
% main convergence loop, assume gaussians are 1D
while ((( abs((step/last_step)-1) > thresh) & (step>(N*eps)) ) | (iter<min_iter) )
% E step
% ========
Q = Z;
P = C ./ (Ic*sqrt(sig2)) .* exp( -((X*Ir - Ic*u).^2)./(2*Ic*sig2) );
for m = 1:M
Z(:,m) = (P(:,m)*t(m))./(P*t(:));
end
% estimate convergence step size and update iteration number
prog_text = sprintf(repmat( '\b',1,(iter>0)*12+ceil(log10(iter+1)) ));
iter = iter + 1;
last_step = step * (1 + eps) + eps;
step = sum(sum(abs(Q-Z)));
fprintf( '%s%d iterations\n',prog_text,iter );
% M step
% ========
Zm = sum(Z); % sum each column
Zm(find(Zm==0)) = eps; % avoid devision by zero
u = (X')*Z ./ Zm;
sig2 = sum(((X*Ir - Ic*u).^2).*Z) ./ Zm;
t = Zm/N;
end
sig = sqrt( sig2 );
给出一个示例:
clc;clear all;close all; set(0,'defaultfigurecolor','w') x = [1*randn(100000,1)+3;3*randn(100000,1)-5]; %fitting x = x(:); % should be column vectors ! N = length(x); [u,sig,t,iter] = fit_mix_gaussian( x,2 ); sig = sig.^2; %Plot figure; %Bar subplot 221 plot(x(randperm(N)),'k');grid on; xlim([0,N]); subplot 222 numter = [-15:.2:10]; [histFreq, histXout] = hist(x, numter); binWidth = histXout(2)-histXout(1); bar(histXout, histFreq/binWidth/sum(histFreq)); hold on;grid on; %Fitting plot subplot 223 y = t(2)*1/sqrt(2*pi*sig(2))*exp(-(numter-u(2)).^2/2/sig(2)); plot(numter,y,'r','linewidth',2);grid on; hold on; y = t(1)*1/sqrt(2*pi*sig(1))*exp(-(numter-u(1)).^2/2/sig(1)); plot(numter,y,'g','linewidth',2);grid on; %Fitting result subplot 224 bar(histXout, histFreq/binWidth/sum(histFreq)); hold on;grid on; y = t(2)*1/sqrt(2*pi*sig(2))*exp(-(numter-u(2)).^2/2/sig(2)); plot(numter,y,'r','linewidth',2);grid on; hold on; y = t(1)*1/sqrt(2*pi*sig(1))*exp(-(numter-u(1)).^2/2/sig(1)); plot(numter,y,'g','linewidth',2);grid on;
结果便是GMM背景介绍中的图形。
类似的,可以参考混合拉普拉斯分布拟合(LMM),对应效果:
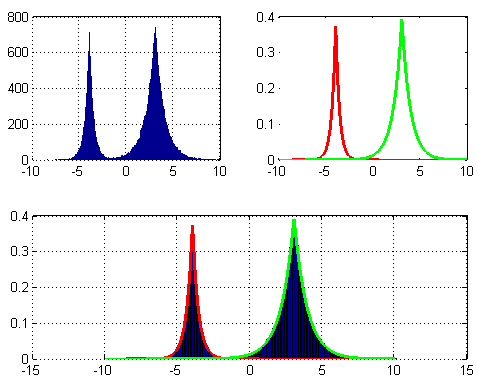
参考:
李航《统计学习方法》.