自适应滤波：随机过程基础
作者：桂。
时间：2017-03-09 21:15:34
链接：http://www.cnblogs.com/xingshansi/p/6527961.html
【读书笔记01】
前言
这几天打算学一学滤波器的相关原理，看的书籍是西蒙.赫金的《自适应滤波器原理》第四版，记录的内容为自己的学习总结，本文主要分为以下四部分：
1）随机过程、确定过程
2）均值、方差、分布函数与概率密度
3）不相关与独立性
4）平稳性与遍历性
内容中不当的地方，还麻烦各位给以指正，内容多有参考他人，对应的链接在文章最后一并给出。
一、随机过程与确定过程
对于一个火车，下一时刻的轨迹已经由铁轨确定了；而对于一个行人，下一刻的落脚点却有各种可能。
简单来说，下一时刻确定的，是确定过程；不确定的，是随机过程。下一刻所有可能，组成了随机变量，即随机变量是各种可能的集合。
给一张示意图：
信号x是一个随机分布，下一刻的值有各种可能；而信号y是一个确定过程，下一刻的值由$y = sin(t)$唯一确定。
既然有各种可能，为什么还要研究随机过程呢？再来一个示意图：
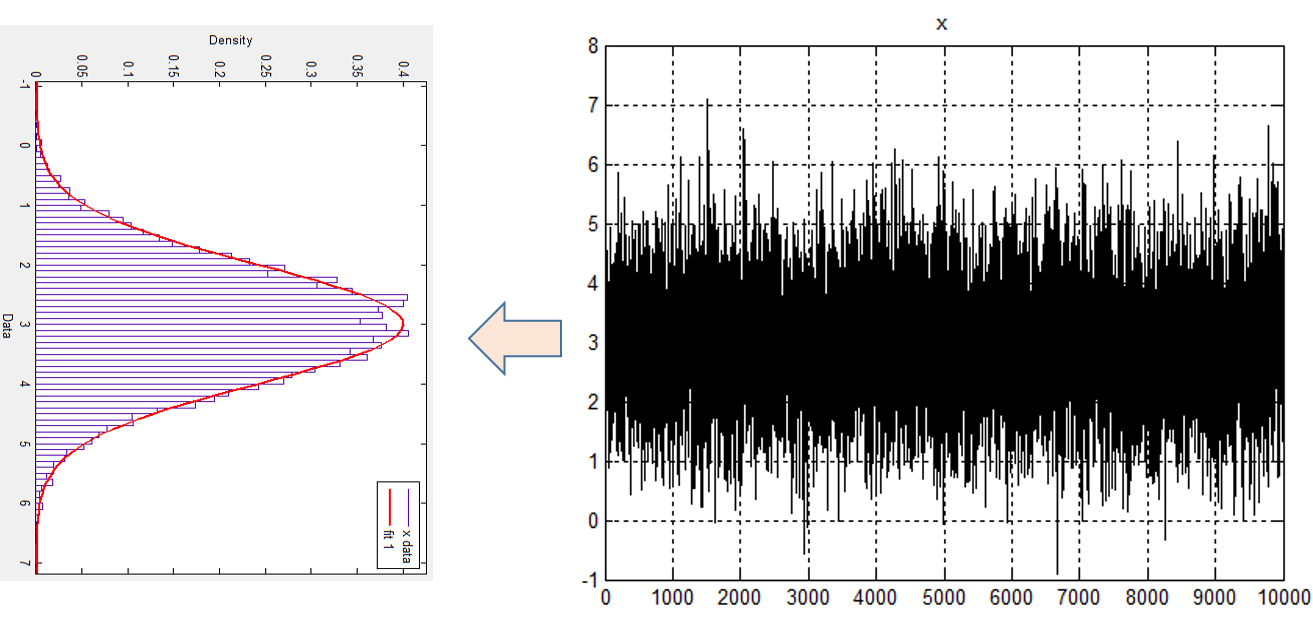
将随机信号x进行直方图统计，通过曲线拟合可以看到：x对应的每一时刻的值都服从正态分布，我们或许可以说：下一时刻，信号x取3的概率大于x取9的概率。由此我们可以相信：对于随机的数据，直方图统计也会包含有价值的信息，so~继续研究它。
二、常用基本概念（针对随机变量描述）
A-均值
给出均值的定义式：
$E[x(t)] = \int_{\; - \infty }^{\; + \infty } {x{f_X}(x\;;t)} dx$
即对于给定时刻t，假设所有的可能都给定了，我们不需要像上一张图那样，需要对不同时刻t进行统计，而是直接对t时刻所有可能值统计，得到分布直方图。利用分布的密度函数，从而实现均值的估计。
现实情况是：我们无法得到同一时刻的所有可能，怎么解决这个尴尬？接着往下看。
B-方差
假设$\mu (t)$是t时刻的均值，则对应的方差定义为：
$D[x(t)] = \int_{\; - \infty }^{\; + \infty } {{{(x - \mu (t))}^2}{f_X}(x\;;t)} dx$
求解同均值类似，尴尬也是。方差体现了数据围绕期望值的分散情况，真是求之不得，辗转反侧，难怪均值叫期望。
知道均值、方差，并不能唯一确定分布（正态是可以的），还需要一些辅助特性来评定统计的分布特性：
- 偏度（Skew）
skew衡量分布的偏斜状况。详细参考：维基百科。
- 峰度（Kurtosis）
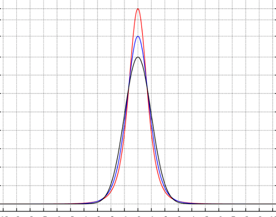
kurtosis衡量分布陡峭状况。详细参考：维基百科。
C-分布函数与概率密度
直接对t时刻所有可能值统计，得到分布直方图，直方图面积归一化，对应的曲线就是概率密度$f(x;t)$,$f(x;t)$关于x的积分就是分布函数$F(x;t)$。
三、不相关与独立性
给一个示意图：
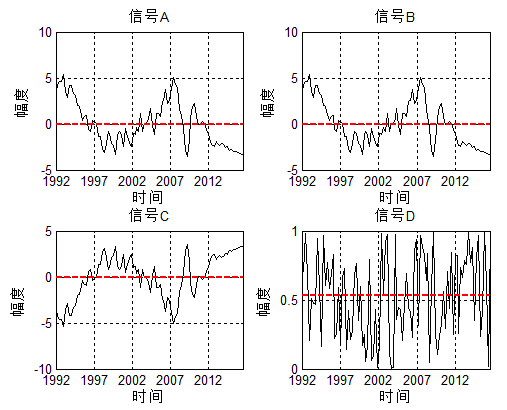
信号A、B、C、D是四个不同的随机信号：
-
- 当信号A增加时，信号B也在增加，A、B的变化趋势完全一致，可以说A与B正相关；
- 当信号A增加时，信号C在减小，A、C的变化趋势完全相反，可以说A与B负相关；
- 当信号A增加时，信号D可能增加，也可能减小，A、D的变化趋势似乎无关，可以说A与B不相关；
给出协方差定义式：
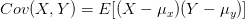
关于相关的细节讨论，可以参考知乎的答案。
相关矩阵虽然体现了相关性，但协方差数值变化时大时小，因此考虑将其归一化（去均值、除均方差）：
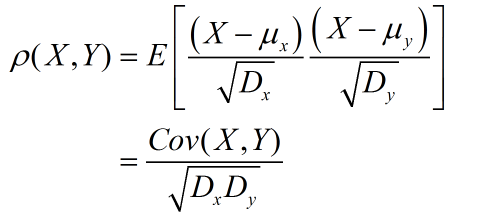
从定义式也可以观察：此处的相关是线性相关，而不是一般意义的相关。因此即使不相关，也不过是线性不相关罢了，说的简单点：A、B两信号不相关，则A的取值变化，不对B的取值产生影响。事实上，A-B-C-D四个信号，是
举个反例：$X$在[-1, 1]上均匀分布，$Y = X^2$，
$Cov(X,Y) = E(X,Y)-E(X)E(Y) = E(X^3) = 0$，即X与Y不相关，可见所谓的相关与否仅仅针对线性，但很明显他们是二次相关，故二者不独立。
给出相关系数为0.9的两个变量的各自曲线，以及联合分布：
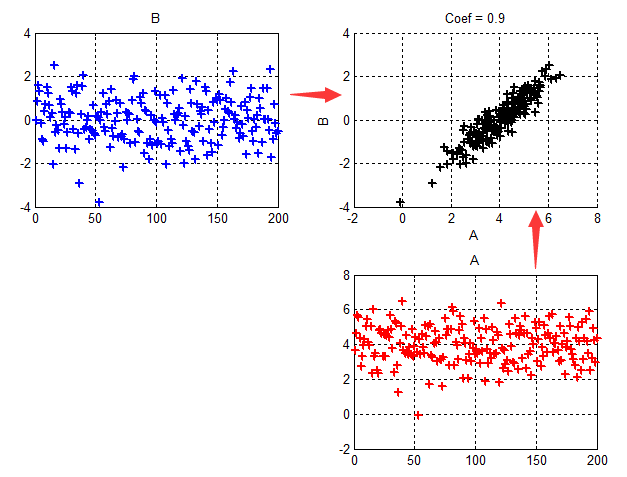
下图从左到右均为联合分布，A、B的相关系数分别为：0.9，-0.9，0，可以看到，以均值为中心，他们对应的正/负/无 线性关系。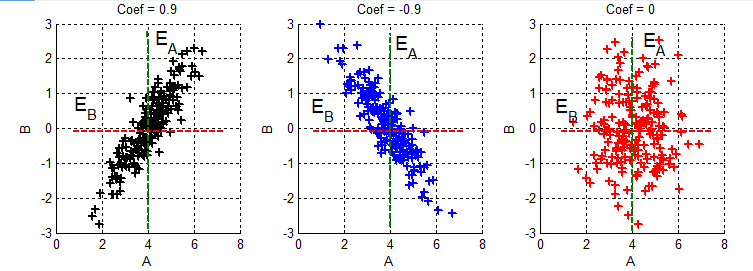
对应的协方差矩阵分别为：${S_1} = \left[ {1,0.9;0.9,1} \right]$, ${S_2} = \left[ {1, - 0.9; - 0.9,1} \right]$, ${S_3} = \left[ {1,0;0,1} \right]$，协方差矩阵的重要性也就不言而喻了。
四、平稳性与遍历性
先来一张图：
对于图中数据，我们不会认为：右边数据服从左边的分布，我们更倾向认为：右图前段数据服从一个分布，后段数据服从一个分布。可以理解为：该信号为非平稳，或者说：短时平稳。
平稳性：就是时间序列统计特性于时间平移的不变性。
翻译一下上面这句话：对于$t_0$时刻，所有可能对应集合Set0，对于$t_1$时刻，所有可能对应集合Set1，...，不同时刻的集合，其统计特性一致。
为什么关于时间需要统计特性不变呢？因为随机变量，取任何值都不确定，只能基于大数据的统计特性进行描述，而如果该时刻或者历史时间段的统计信息，对下一时刻没有任何的借鉴意义，即：统计特性只对统计数据自身成立，统计的意义又在哪里呢？
A-严平稳
严平稳需要统计性质关于之间严格不变，给出定义：
对于所有可能的n，所有可能的$t_1,t_2, ... t_n$和所有可能的k, 当$Z_{t1},...Z_{tn}$和$Z_{t1-k},...Z_{tn-k}$相同时，我们称其为严平稳.
基于两点，我们通常不用该特性：
- 不同时刻，一阶矩、二阶矩...N阶矩，完全一致，则该过程为严平稳，计算量太大，甚至没有终止；
- 常用的统计特性是均值、协方差矩阵，这个只涉及二阶矩，满足通常的需求；
这也是为什么宽/弱平稳，是均值、方差的一致性，而不必三阶矩、四阶矩一致的原因之一。
B-弱/宽平稳
上面已经略有提及，在此给出宽平稳的特性：
- 期望不随时间变化，是常数；
- 协方差函数仅与时间差有关，与时间的具体时刻无关
我们称这样的过程为宽平稳随机过程。
为什么这么定义？举个例子：
设序列{$X_1, X_2, X_3...$}，是互不相关的随机变量序列，且都~N（0，${\sigma ^2}$），则
这就是一个宽平稳的例子，其实第二个特性就是对二阶矩的限定。
啰嗦一句：
- 分布一致，则矩一定一致，故严平稳一定是宽平稳（错，因为矩可能不存在，存在时则一定是）。
- 联合分布服从多元正态分布时，二者等价，因为二阶矩已经完全可以确定正态分布
C-遍历性
遍历性，即各态历经性，真是顾名思义。还记得上文的尴尬么？一个时刻的所有可能，现实中天知道会是什么？
除非这样：
数量足够多的机器，假设10万台，性能完全一致，同时刻工作，同时刻停止，将这样一个小的时间段认为一个时间点，然后统计机器损坏的数量M，
故障率为 = M/100000；
这样基于大样本的统计特性，近似可以看作其分布特性，但这里有两个困难：
1）性能完全一致，这个本身就做不到；2）现实中，很难有同一时刻，样本集合几乎遍历的情况；
能不能折中一下呢？假设一段时间内，所有可能的集合元素，都发生了（即遍历），利用时间统计特性，近似等价。嗯，用时间换空间，是个不错的主意。
遍历性对于时间序列的意义，类似于大数定理对于一般随机变量的意义。
首先回顾一下：对于一个时间序列{$X_t，t = 1,2,...$}，样本均值如何定义：
$\mu = \frac{1}{T}\sum\limits_{t = 1}^T {{x_t}} $
（Eq-1）
其中$x_t$为时间序列$X_t$的一条路径，不妨设为某个股票的日收益率。
样本自相关函数、样本自相关系数等等，类似。
即：实际应用中，用样本的时间均值，代替集合的统计均值，即对于某个时刻的所有可能，我们认为这些可能在一段时间内，会全部出现，这就是遍历性，也叫各态历经性。
回顾大数定律：
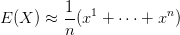（Eq-2）
Eq-1是时间取均值，Eq-2是空间取均值。可以说，随机过程遍历性假设若不成立，应用中的统计总是管中窥豹，就像调研中的小样本，得出的结论看似严谨，实则荒谬。
参考：
