信号处理——信号频域变换
作者:桂。
时间:2017-03-07 18:40:05
链接:http://www.cnblogs.com/xingshansi/p/6516256.html
声明:欢迎转载,不过记得注明出处哦~

前言
本文主要介绍信号频域变换的常用方式,主要介绍基本的三种方法,实现时域数字信号的傅里叶变换:
1)基本DFT变换;
2)FFT变换
3)逆序级联FFT
三种方法实现方式略有差别,但本质完全相同。为了方便大家理解,本文给出基本MATLAB实现。内容的理论部分,多有借鉴他人,相应链接在最后一并给出。
〇、写在前面
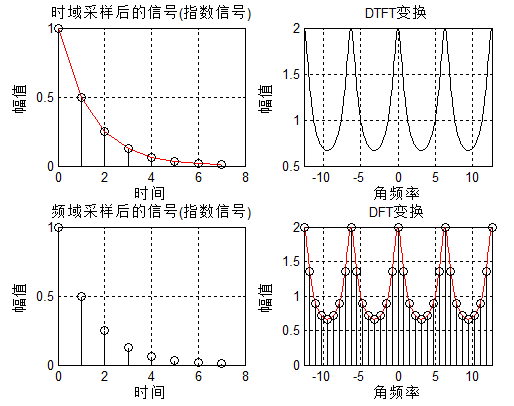
关于信号时域连续、离散以及各自频域的对应关系,可以参考之前的一篇博文。为了便于理解,此处给一个DTFT—>DFT的解释。
MATLAB代码:
%DTFT
clc;clear all;close all
N=8; %原离散信号有8点
n=[0:1:N-1] ; %原信号是1行8列的矩阵
xn=0.5.^n; %构建原始信号,为指数信号
w0=[-2*N:.1:2*N]*2*pi/N; %方便观察,此处取4个周期-4*pi~4*pi
X0=xn*exp(-j*(n'*w0)); %求dtft变换,采用原始定义的方法,对复指数分量求和而得
subplot(221)
plot(n,xn,'r');hold on;xlabel('时间')
stem(n,xn,'k');grid on;
title('时域采样后的信号(指数信号)');ylabel('幅值')
subplot(222);
plot(w0,abs(X0),'k');ylabel('幅值');xlabel('角频率');%逼近连续,其实这么处理不正确,仅仅是方便理解
title('DTFT变换');
xlim([-4*pi,4*pi]);grid on;
%DFT
w=[-2*N:1:2*N]*2*pi/8;
X=xn*exp(-j*(n'*w)); %对DTFT进行频域采样
subplot(223)
stem(n,xn,'k');ylabel('幅值');xlabel('时间');grid on;
title('频域采样后的信号(指数信号)');
subplot(224);
plot(w0,abs(X0),'r');hold on;
stem(w,abs(X),'k');ylabel('幅值');xlabel('角频率')
title('DFT变换');
xlim([-4*pi,4*pi]);grid on;
对应结果图:
一、基本DFT变换
DFT变换有:
$F(k) = \sum^{N-1}_{n=0} f(n) e^{\frac{-j2\pi kn}{N}}$
写成矩阵的形式:
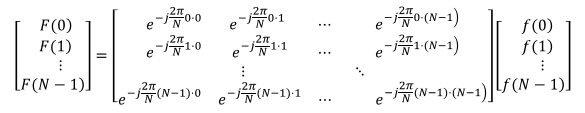
对应的转换为VanderMonde矩阵,对应的MATLAB代码:
clc;clear all;close all;
fs = 200;
f0 = 30;
t = 0:1/fs:2;
x = sin(2*pi*f0*t');
N = length(x);
%DFT
X_DFT = exp(-j*2*pi/N).^([0:N-1]'*[0:N-1])*x;
%绘图
xf = linspace(0,fs,N);
plot(xf,abs(X_DFT),'k');grid on;
xlabel('频率(Hz)');
ylabel('幅度');
title('DFT结果');
也可以将DFT的代码换为Vander矩阵形式,只需修改一句:
% X_DFT1 = exp(-j*2*pi/N).^([0:N-1]'*[0:N-1])*x; %修改为下句 X_DFT = fliplr(vander(exp(-j*2*pi/N).^([0:N-1]))).'*x;
结果图:

二、FFT变换
DFT到FFT常用的有奇偶抽取/前后抽取,两种实现方式,原理此处不再堆砌,可以参考维基百科:
- FFT:https://en.wikipedia.org/wiki/Fast_Fourier_transform
- Cooley-Tukey FFT:https://en.wikipedia.org/wiki/Cooley%E2%80%93Tukey_FFT_algorithm
给出对应的MATLAB代码:
clc;clear all;close all;
fs = 200;
f0 = 30;
t = 0:1/fs:2;
x = sin(2*pi*f0*t');
N = length(x);
%FFT
X_FFT = fft(x);
%绘图
xf = linspace(0,fs,N);
plot(xf,abs(X_FFT),'k');grid on;
xlabel('频率(Hz)');
ylabel('幅度');
title('FFT结果');
结果图:
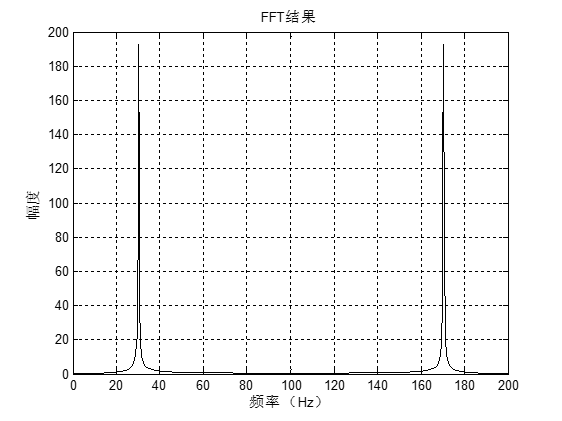
如果严格按照FFT定义,则应该将序列补为$2^N$长度(事实上,内置fft自动完成此操作),代码修改为:
clc;clear all;close all;
fs = 200;
f0 = 30;
t = 0:1/fs:2;
x = sin(2*pi*f0*t');
N = length(x);
%FFT
Len = 2^nextpow2(length(x));
X_FFT = fft(x,Len);
%绘图
xf = linspace(0,fs,Len);
plot(xf,abs(X_FFT),'k');grid on;
xlabel('频率(Hz)');
ylabel('幅度');
title('FFT结果');
对应结果图:

三、逆序级联FFT
为了方便,假设信号$f(n)$长度为2的整次幂。对于数据量过大的情况,可以通过串/并的不断转化,对数据进行分流,从而利用多个芯片实现一个大芯片的任务(此处为个人理解,仅供参考)。给出对应的流图:

以及具体的推导公式:
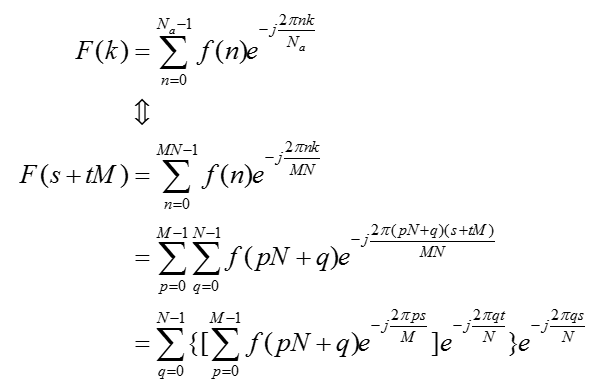
步骤可以简化为:分段FFT,即公式[.]部分—>因子补偿,即公式{.}部分—>分段FFT,即公式最外层部分。
给出具体的实现代码:
clc;clear all;close all;
fs = 200;
f0 = 30;
t = 0:1/fs:2;
x = sin(2*pi*f0*t');
Na = 2^nextpow2(length(x));
sig = [x;zeros(Na-length(x),1)];
N=16;M=Na/N;
sr=zeros(M,N);
for m=1:M
sr(m,:)=sig((m-1)*N+1:m*N,1);
end
for n=1:N
sr(:,n)=fft(sr(:,n));
end
P=zeros(M,N);
for p=0:M-1
for n=0:N-1
P(p+1,n+1)=exp(-j*2*pi*n*p/M/N);
end
end
sr=sr.*P;
for m=1:M
sr(m,:)=fft(sr(m,:));
end
%save result
X_CaFFT = zeros(length(sig),1);
for n=1:N
X_CaFFT((n-1)*M+1:n*M,1)=sr(:,n);
end
%绘图
xf = linspace(0,fs,Na);
plot(xf,abs(X_CaFFT),'k');grid on;hold on;
xlabel('频率(Hz)');
ylabel('幅度');
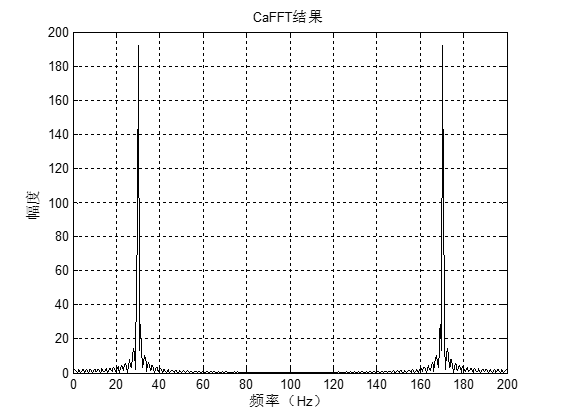
title('CaFFT结果');
对应结果图:
四、三种算法对比分析
三种结果效果完全等价,分析其各自性能。
对于快速运算中,一个蝶形运算,对应一个乘法,两次加法。
| DFT | FFT | CaFFT | |
| 加法器 | $N^2$ | $N log_2N$ | $N log_2N+N$ |
| 乘法器 | $N(N-1)$ | $2Nlog_2N$ | $2Nlog_2N$ |
可见FFT所需资源最少,但如果数据量过大导致直接FFT,硬件无法满足条件,则CaFFT是最优的选择。
参考:
郑君里:《信号与系统》第二版;
张大炜:一种新的级联FFT算法.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号