FFT节省资源的思路

作者：桂。

时间：2017-01-18  23:07:50

链接：http://www.cnblogs.com/xingshansi/articles/6298391.html 

---

前言

 FFT是信号处理的常用手段，许多应用场景同时需要两个甚至多个傅里叶变换结果。例如：计算输入信号通过一个系统的输出结果，为了进行快速运算，通常需要利用补零操作使得二者长度相同，并借助FFT实现。许多场景中输入信号以及滤波器冲激响应都为实数，本文主要分析如何通过一个FFT运算同时得出两个实数DFT的结果。

 一、利用一组复数FFT实现两组实数FFT

　　A.模型构造

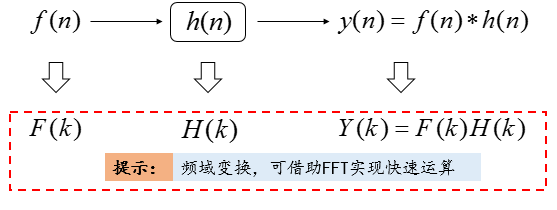
图1 本文理论的应用场景示意图

应用需求如图1所示，定义新变量$z(n)$:

$z(n)= f(n) + jh(n)$

$z(n)$对应的频域变换为：

$Z(k)=X(k)+jH(k)$

 

　　B.理论推导

对于信号$z(n)$以及其共轭信号，

$z(n)=f(n)+jh(n)$
$z^*(n)=f(n)-jh(n)$

对应的频域变换为：

$Z(k)=F(k)+jH(k)$
$Z^*(k)=F(k)-jH(k)$

又信号$z^*(n)$的频域变换存在如下性质，

$DFT(z^*(n))=\sum^{N-1}_{n=0}z^*(n)e^{-\frac{j2\pi kn}{N}}= Z^*(N-k)$

从而由一个FFT运算得到两个FFT结果：

$F(k)=\frac{Z(k)+Z^*(N-k)}{2}$
$H(k)=\frac{Z(k)-Z^*(N-k)}{2j}$

当然输出结果也可以直接得出

$Y(k)=F(k)H(k)=\frac{[Z(k)]^2-[Z^*(N-k)]^2}{4j}$

对于N点的FFT，对应复数乘法个数为：

• 基2FFT：N/2*log₂(N)
• 基4FFT：N/2*log₂(N)-N

二、复数乘法的变形

对于两个复数：x1 = a+jb;  x2 = c+jd：

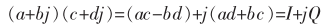
进一步变形：

可以看出I、Q的第一项是相同的，这样便实现了：复数乘法由4个实数乘法器组成，简化为复数乘法由3个实数乘法器组成。