信号处理——傅里叶变换(FT-DTFT-DFT)
作者:桂。
时间:2017-01-17 23:41:13
链接:http://www.cnblogs.com/xingshansi/articles/6294111.html
前言
信号处理一个重要的关系就是时域与频域的关系,本专题为:信号处理的频域处理。
本文主要讲述信号从时域连续信号到数字信号的变化,以及对应的频域关系,内容较为基础,公式不作具体推导。
更多详细的理论以及对应MATLAB代码,可以参考另一篇博文。
理论分析
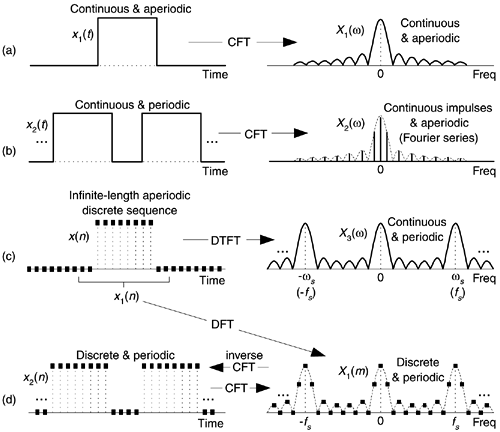
(图1 信号的时频对应关系)
A.傅里叶变换(FFT)
由图1(a)可以看出,连续非周期时域连续信号,对应频域信号仍然是连续信号。
对应的变换关系为:
时域——>频域
$F(\omega) = \int^{+\infty}_{-\infty} f(t) e^{-j\omega t}dt$
频域——>频域
$f(t) = \frac{1}{2\pi}\int^{+\infty}_{-\infty} F(\omega) e^{j\omega t}dt$
图1(b)为傅里叶级数,此处不作描述。
B.离散时间傅里叶变换(DTFT)
图1(c)表示对图1(a)在时域上进行采样,得到时域的离散信号,对应的频域信号仍然是连续信号,并且是以采样率为周期的周期信号。
对应的变换关系为:
时域——>频域
$F(e^{j\omega}) = \sum^{+\infty}_{-\infty} f(n) e^{-j\omega n}$
频域——>时域
$f(n) =\frac{1}{2\pi} \sum^{+\pi}_{-\pi} F(e^{j\omega}) e^{j\omega n}$
C.离散傅里叶变换(FFT)
图1(d)表述对图1(c)在频域上进行采样,得到的时域离散信号,对应的频域也变为离散信号。
对应的变换关系为:
时域——>频域
$F(k) = \sum^{N-1}_{n=0} f(n) e^{\frac{-j2\pi kn}{N}}$
频域——>时域
$f(n) = \frac{1}{N}\sum^{N-1}_{k=0} F(k) e^{\frac{j2\pi kn}{N}}$
三种变换的关系总结一下,关系如图2所示。至于FFT,是DFT的蝶形运算,本质相同,仅仅是运算不同,这里只是分析信号变换的对应关系,FFT的原理不作讨论。

(图2 三种变换的对应关系)


