【learning】微信跳一跳辅助c++详解 轻松上万 【上】
写在前面
17年年底Wechat出了这个跳一跳的小游戏,今年2月份的时候简单地玩了一下,发现被游戏虐了(手太残了只能跳20多)。
今天刚好有点空,于是就花了一个下午的时间写了一个跳一跳的c++辅助。
由于本OIER既不会Python,也不会安卓的USB调试,更不会单片机,故写了一一个操作安卓模拟器的辅助。
先放下效果:(只是先截个图而已,截止至目前跳了2150次,运行1小时55分钟)【未完待续】
据之前的跳一跳大赛的结果,尽管人类的第一为1.2W分,但仍被本半天速成辅助轻松碾在地上。
--------------------------------------------------------------------------------我是分割线-----------------------------------------------------------------------------------------------
一些最基础的东西
完成一次跳跃,你需要得到棋子位置及方块位置。进而计算出两者之间的距离,随后跳跃相应的距离。
在我尚不了解跳一跳底层的数据的时候,抓屏分析几乎是唯一选项。
所以你要先完成抓屏。
如何抓屏
在不额外导库的情况下,windows.h下提供了一个函数叫做getpixel,然而这个函数效率过低,显然不合适如此大面积的图像处理。
然而我又比较懒,不想去装库,但碰巧手头有我半年前手写的bmp库。
我从网上找了个快捷键自动截屏的小程序,通过发送快捷键将屏幕数据转为bmp存入磁盘,再用bmp读取(捂脸)。
反正这种简单游戏对辅助的吞吐量要求不高,就先这么凑合着用吧....
代码就不单独拎出来了
完成抓屏后,为了能够实现准确地识别棋子位置及方块位置,我们要先对界面做一些处理。
显然,我们要把背景和图形阴影给过滤掉。
经过多次抓屏分析,我们得到了跳一跳背景和阴影的一些特征:
1,对于同行不同列,阴影部分的RGB数据完全相同,背景部分的RGB数据也完全相同,且阴影的RGB数据=背景的RGB数据/k (k约等于1.4356)
2,杜宇不同行的同列,背景部分的RGB数据可能不同,且对于全部行,$\Delta R,\ \Delta G,\ \Delta B≤50$。
我们基于这两个性质,对游戏界面进行背景和阴影过滤。
如图所示,过滤前与过滤后。(请先无视除背景颜色变化外的所有东西)


【实现方法】
我们对于每一行分开处理,对于一个正在处理的行,找出该行内出现次数最多的颜色,随后通过计算算出该行阴影的rgb数据。随后将这两种颜色的像素设为黑色(#000000)
该方法的缺点也是显而易见的,首先,无法过滤阴影的边框,且对于方块分布较密集的部分,该过滤方式可能会出现一些问题。
所幸的是,不过滤边框几乎不会影响到接下来的判定,且目标点附近不会出现许多个方块(仅1个嘛....)
滤色部分代码:
1 for(int i=1;i<=P.n;i++){ 2 mp.clear();//该map用于判断颜色众数,由于对吞吐量要求不高,故没有进一步优化 3 for(int j=1;j<=P.m;j++) 4 mp[node(P.r[i][j],P.g[i][j],P.b[i][j])]++; 5 map<node,int>::iterator it; 6 node maxid,maxid2; int maxn=0; 7 for(it=mp.begin();it!=mp.end();it++){ 8 if(maxn<it->second){ 9 maxn=it->second; 10 maxid=it->first; 11 } 12 } 13 maxid2.r=maxid.r/conY;//cony即为上文所说的某个常数 14 maxid2.g=maxid.g/conY; 15 maxid2.b=maxid.b/conY; 16 for(int j=1;j<=P.m;j++){ 17 if(maxid.cmp(P.r[i][j],P.g[i][j],P.b[i][j])) 18 P.r[i][j]=P.g[i][j]=P.b[i][j]=0; 19 if(maxid2.cmp(P.r[i][j],P.g[i][j],P.b[i][j])) 20 P.r[i][j]=P.g[i][j]=P.b[i][j]=0; 21 } 22 }
如何找到棋子
笔者通过简单地分析,发现棋子的色域非常特殊,几乎不存在与棋子相同颜色的方块。
根据此特征,我们只需要求出在特定色域内的点所构成的点集,随后对这些点求一个平均坐标,再加上一个常数项的偏移,即可求出棋子的近似坐标。
用于判定点集的色域:$R∈[43,68],G∈[49,57],B∈[76,102]$。
捕捉到的棋子:
被染成灰色的部分为在色域内的点,白色点即为所有灰色点的平均加偏坐标。
经过近万次实际捕捉,可以证明大胆猜想该方法是有效的。
代码如下:
1 #define LR 43 2 #define RR 68 3 #define LG 49 4 #define RG 57 5 #define LB 76 6 #define RB 102 7 8 int sumx=0,sumy=0,cntx=0; 9 for(int i=1;i<=P.n;i++) 10 for(int j=1;j<=P.m;j++){ 11 int dR=abs(P.r[i][j]); 12 int dG=abs(P.g[i][j]); 13 int dB=abs(P.b[i][j]); 14 int cnt=0; 15 if(LR<=dR&&dR<=RR) cnt++; 16 if(LG<=dG&&dG<=RG) cnt++; 17 if(LB<=dB&&dB<=RB) cnt++; 18 if(cnt==3){ 19 P.r[i][j]=P.g[i][j]=P.b[i][j]=100; 20 sumx+=i; sumy+=j; cntx++; 21 } 22 }//识别棋子
如何确定目标点
我们先大胆假设,我上一次跳到了中心点!!!
我们不难发现,在下个方块的正中心,出现了大大的白点?
经过反复的抓屏,我们发现这个白点具有以下几个性质:
1,永远在目标的正中心。
2,除了边界颜色与目标本身稍有混合外,其余部分相同且不变(#F1F1F1)
3,该点不变色部分的颜色具有近似唯一性(除了药瓶瓶口附近外,其余的格子均不会出现这种颜色,包括看起来很白的几个方块)。
基于这三个特性,我们不妨大胆猜出一个抓白点的方法:
在全屏范围内搜索,是否存在一个色块,满足其大小为12*8px,且颜色均为#F1F1F1。
通过多次测试可以发现满足此条件的色块均在白点内,药瓶子是找不到这样的位子的。
在符合条件的色块中,任意选出一个色块,则目标点的坐标即为该色块的中点(因为色块数量非常少,且非常集中,经测试该方法偏移仅为±2px,和因模拟器卡顿造成的偏移已相差无几,故几乎不用担心精度问题)。
由于存在机器卡顿,误差累计等问题,故无法保证每次跳跃均落在中心点(目前中心率为89.1%),目前最好的记录是连续50次跳到中心点。
这个记录,我相信不采用辅助人手是完全无法做到的。
代码:
1 CAP.readfile("0000white.bmp");//对白点的特殊优化,由于赶工,采用了直接读取bmp的方法 2 int minn=1234567890,maxx=0,maxy=0; 3 for(int j=chessX;j>=chessX-300;j--) 4 for(int i=1;i<=P.m-CAP.m;i++){ 5 int sum=0,pcnt=0; 6 for(int ii=1;ii<CAP.m;ii++) 7 for(int jj=1;jj<CAP.n;jj++){ 8 sum+=pf(P.r[j+jj][i+ii]-CAP.r[jj][ii]); 9 sum+=pf(P.g[j+jj][i+ii]-CAP.g[jj][ii]); 10 sum+=pf(P.b[j+jj][i+ii]-CAP.b[jj][ii]); 11 } 12 if(sum==0){ 13 minn=sum,maxx=i,maxy=j; 14 break; 15 } 16 } 17 //cout<<minn<<endl; 18 if(minn==0){ 19 printf("catch white point!\n"); 20 for(int ii=1;ii<CAP.m;ii++) 21 for(int jj=1;jj<CAP.n;jj++){ 22 P.r[maxy+jj][maxx+ii]=0; 23 P.g[maxy+jj][maxx+ii]=255; 24 P.b[maxy+jj][maxx+ii]=0; 25 } 26 TX=maxy+6; TY=maxx+8; 27 P.r[TX][TY]=255; P.g[TX][TY]=P.b[TX][TY]=0; 28 // P.outfile("test.bmp"); 29 return 2; 30 }
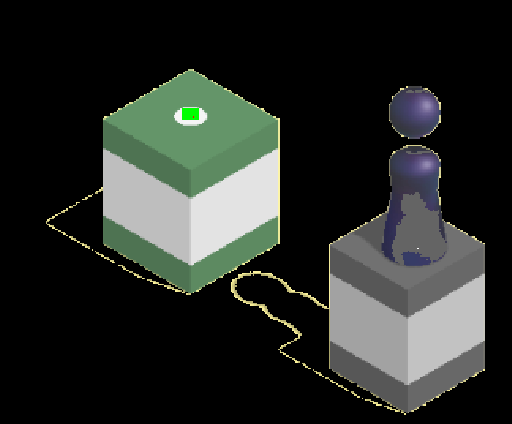

绿色的位置即为匹配到的白点,红点为预计落点
然而,不幸的是,还是有11%的概率跳不到中心点上,下面我们就要采用另一套算法来解决问题:
我们不妨假设这棋子在屏幕的左半边,且我们已知棋子的中心坐标。
我们以棋子为原点,以正右方向为X轴正半轴构造笛卡尔坐标系。
通过简单地统计,我们不难发现目标的位置大概在$f(x)=tan \frac{\pi}{6}x$上
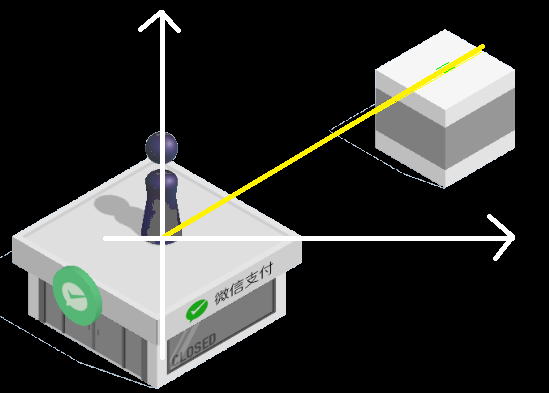

于是我们构造五条射线$f(x)=tan \frac{\pi}{6}x-10$,$f(x)=tan \frac{\pi}{6}x-5$,$f(x)=tan \frac{\pi}{6}x$(图中画出了这一条),$f(x)=tan \frac{\pi}{6}x+5$,$f(x)=tan \frac{\pi}{6}x+10$,将在线上的所有像素取出。
随后,我们找出出现次数最多的颜色,对所有该颜色像素求一个平均坐标,即可得到目标点位置。
考虑到该游戏中存在有花纹较多的方块(如437天,木纹小板凳),我们钦定一个常数eps(允许误差范围),求出像素数量最多的色域(可以理解为$R∈[r-eps,r+eps],G∈[g-eps,g+eps],B∈[b-eps,b+eps]$)求出该色域内所有像素的平均坐标,得到目标点。
如上方右图所示,被染成绿色的点即为判定点,中心红点即为预计落点。
为了提升精度,eps会根据出现的颜色数量而做出相应的调整。
本辅助中,设置了4个阈值5个eps。
对于棋子在屏幕右半边的情况同理。
代码:
1 memset(X,0,sizeof(X)); memset(Y,0,sizeof(Y)); 2 memset(lineR,0,sizeof(lineR)); memset(lineG,0,sizeof(lineG)); memset(lineB,0,sizeof(lineB)); 3 //loop:; 4 mp.clear(); 5 if(chessY<=290 ){ 6 for(int i=chessY+60;i<=P.m;i++){//绘制函数 7 int j=chessX-(i-chessY)*tan30; 8 if(P.r[j][i]==0&&P.g[j][i]==0&&P.b[j][i]==0) continue; 9 cnt++; 10 lineR[cnt]=P.r[j][i]; 11 lineG[cnt]=P.g[j][i]; 12 lineB[cnt]=P.b[j][i]; 13 X[cnt]=j; Y[cnt]=i;//将函数上的点加入集合中,下文同理 14 mp[node(P.r[j][i],P.g[j][i],P.b[j][i])]++; 15 cnt++; 16 lineR[cnt]=P.r[j-4][i]; 17 lineG[cnt]=P.g[j-4][i]; 18 lineB[cnt]=P.b[j-4][i]; 19 X[cnt]=j-4; Y[cnt]=i; 20 mp[node(P.r[j-4][i],P.g[j-4][i],P.b[j-4][i])]++; 21 cnt++; 22 lineR[cnt]=P.r[j+4][i]; 23 lineG[cnt]=P.g[j+4][i]; 24 lineB[cnt]=P.b[j+4][i]; 25 X[cnt]=j+4; Y[cnt]=i; 26 mp[node(P.r[j+4][i],P.g[j+4][i],P.b[j+4][i])]++; 27 cnt++; 28 lineR[cnt]=P.r[j+8][i]; 29 lineG[cnt]=P.g[j+8][i]; 30 lineB[cnt]=P.b[j+8][i]; 31 X[cnt]=j+8; Y[cnt]=i; 32 mp[node(P.r[j+8][i],P.g[j+8][i],P.b[j+8][i])]++; 33 cnt++; 34 lineR[cnt]=P.r[j-8][i]; 35 lineG[cnt]=P.g[j-8][i]; 36 lineB[cnt]=P.b[j-8][i]; 37 X[cnt]=j-8; Y[cnt]=i; 38 mp[node(P.r[j-8][i],P.g[j-8][i],P.b[j-8][i])]++; 39 P.r[j+1][i]=P.r[j-1][i]=255; 40 P.g[j+1][i]=P.g[j-1][i]=255; 41 P.b[j+1][i]=P.b[j-1][i]=0; 42 } 43 }else{ 44 for(int i=chessY-60;i;i--){ 45 int j=chessX-(chessY-i)*tan30; 46 if(P.r[j][i]==0&&P.g[j][i]==0&&P.b[j][i]==0) continue; 47 cnt++; 48 lineR[cnt]=P.r[j][i]; 49 lineG[cnt]=P.g[j][i]; 50 lineB[cnt]=P.b[j][i]; 51 X[cnt]=j; Y[cnt]=i; 52 mp[node(P.r[j][i],P.g[j][i],P.b[j][i])]++; 53 cnt++; 54 lineR[cnt]=P.r[j-4][i]; 55 lineG[cnt]=P.g[j-4][i]; 56 lineB[cnt]=P.b[j-4][i]; 57 X[cnt]=j-4; Y[cnt]=i; 58 mp[node(P.r[j-4][i],P.g[j-4][i],P.b[j-4][i])]++; 59 cnt++; 60 lineR[cnt]=P.r[j+4][i]; 61 lineG[cnt]=P.g[j+4][i]; 62 lineB[cnt]=P.b[j+4][i]; 63 X[cnt]=j+4; Y[cnt]=i; 64 cnt++; 65 mp[node(P.r[j+4][i],P.g[j+4][i],P.b[j+4][i])]++; 66 lineR[cnt]=P.r[j+8][i]; 67 lineG[cnt]=P.g[j+8][i]; 68 lineB[cnt]=P.b[j+8][i]; 69 X[cnt]=j+8; Y[cnt]=i; 70 cnt++; 71 mp[node(P.r[j+8][i],P.g[j+8][i],P.b[j+8][i])]++; 72 lineR[cnt]=P.r[j-8][i]; 73 lineG[cnt]=P.g[j-8][i]; 74 lineB[cnt]=P.b[j-8][i]; 75 X[cnt]=j-8; Y[cnt]=i; 76 mp[node(P.r[j-8][i],P.g[j-8][i],P.b[j-8][i])]++; 77 P.r[j+1][i]=P.r[j-1][i]=255; 78 P.g[j+1][i]=P.g[j-1][i]=255; 79 P.b[j+1][i]=P.b[j-1][i]=0; 80 } 81 } 82 //printf("colorsum:%d\n",mp.size()); 83 if(mp.size()<40){ 84 JumpepsR=JumpepsG=JumpepsB=1; 85 }else if(mp.size()<100){ 86 JumpepsR=JumpepsG=JumpepsB=4; 87 }else if(mp.size()<400){ 88 JumpepsR=JumpepsG=JumpepsB=7; 89 }else JumpepsR=JumpepsG=JumpepsB=10; 90 if(cnt==0) 91 return 1; 92 //if(cnt==0) goto loop; 93 int maxn=0,maxid=0,quan=3; 94 for(int i=1;i<=cnt;i++){ 95 quan=3; 96 int R=lineR[i]; 97 int G=lineG[i]; 98 int B=lineB[i]; 99 int sum=0; 100 for(int j=1;j<=cnt;j++){ 101 int DeltaR=abs(lineR[j]-R); 102 int DeltaG=abs(lineG[j]-G); 103 int DeltaB=abs(lineB[j]-B); 104 if(DeltaR>JumpepsR) continue; 105 if(DeltaG>JumpepsG) continue; 106 if(DeltaB>JumpepsB) continue; 107 sum+=abs(X[j]-chessX)*0.05+4; //求出最大的色域 108 } 109 if(sum>maxn) maxn=sum,maxid=i; 110 } 111 int sumX=0,sumY=0,sum=0; 112 int R=lineR[maxid]; 113 int G=lineG[maxid]; 114 int B=lineB[maxid]; 115 for(int j=1;j<=cnt;j++){ 116 int DeltaR=abs(lineR[j]-R); 117 int DeltaG=abs(lineG[j]-G); 118 int DeltaB=abs(lineB[j]-B); 119 if(DeltaR>JumpepsR) continue; 120 if(DeltaG>JumpepsG) continue; 121 if(DeltaB>JumpepsB) continue; 122 sum++; 123 P.r[X[j]][Y[j]]=0; 124 P.g[X[j]][Y[j]]=255; 125 P.b[X[j]][Y[j]]=0; 126 sumX+=X[j]; sumY+=Y[j];//求出该色域内点出现的最大次数 127 } 128 if(sum==0) 129 return 1; 130 sumX/=sum; sumY/=sum;//求出坐标 131 //求出目标点坐标 132 P.r[sumX][sumY]=255; P.g[sumX][sumY]=P.b[sumX][sumY]=0; 133 TX=sumX; TY=sumY;
找到坐标后,如何确定按压的时长
我们不妨猜想这个按压时间与两点间距呈线性关系。
通过简单地采样+散点图,于是就拟合出了该直线的斜率。
通过该方法,得到的跳跃时间$T=2.55 \times dist$,其中$dist$表示起点到终点的距离,单位为像素,T的单位为毫秒。
后来,我发现该拟合方法误差较大,只能实现连续36次跳至中心点,中心点率为85%。
为了进一步提高精度,我又发现了一个性质:需要跳跃的时间与dist并无直接关联,但与dist在$y=tan \frac {\pi}{6}x$上的投影有关。
因此,优化算法如下:
令向量$\vec a=BEGIN-END$,其中BEGIN表示棋子中心点坐标,END表示目标点坐标。
设一个单位向量$\vec b=(cos \frac{\pi}{6},sin \frac{\pi}{6})$
则跳跃时间$T=2.53 \times \vec a \cdot \vec b$ ,单位仍为毫秒。
再简单地调下参,就可以实现90%的中心点率,最高连续50次中心点啦~。
刚刚跳到4.4W挂掉了....本蒟蒻修复完bug了...
若要看二代辅助的细节,请移步下篇
整个一代辅助代码如下:
#include<bits/stdc++.h> #include<cmath> #include<windows.h> #define d(x) keybd_event(x,0,0,0) #define u(x) keybd_event(x,0,2,0) #define s(x) Sleep(x) #define me(x) mouse_event(x,0,0,0,0) #define sc(x,y) SetCursorPos(x,y) #define gk(x) GetAsyncKeyState(x) #define M 100000 using namespace std; int up(int x){while((x*3)%4!=0) x++;return x;} int lf(int x){return abs(x);} void printhead(unsigned char c[],int n,int m){ //该函数用于写入一个24位bmp头 c[0]=0x42; c[1]=0x4d; //BM unsigned siz=54+3*up(n)*up(m); for(int i=2;i<=5;i++){ c[i]=siz&255; siz=siz>>8; }//写入siz siz=3*n*m; c[10]=0x36;//写入数据头位置 c[0x0e]=0x28;//头大小 for(int i=0x12;i<=0x15;i++) c[i]=m&255,m>>=8;//写入宽度 for(int i=0x16;i<=0x19;i++) c[i]=n&255,n>>=8;//写入高度 c[0x1a]=1;//永远为1 c[0x1c]=0x18;//24位位图 //for(int i=0x22;i<=0x25;i++) c[i]=siz&255,siz>>=8;//写入去头字节数 } #define MFLONG 15000000 #define W 1921 #define H 1081 unsigned char _c[MFLONG]={0}; struct board{//画布函数 int n,m;//宽高 unsigned char r[H][W],g[H][W],b[H][W]; board(){ n=m=0; memset(b,0,sizeof(b)); memset(r,0,sizeof(r)); memset(g,0,sizeof(g)); } board(int nn,int mm,int R,int G,int B){ n=nn; m=mm; memset(b,B,sizeof(b)); memset(r,R,sizeof(r)); memset(g,G,sizeof(g)); } void clear(){ n=m=0; memset(b,0,sizeof(b)); memset(r,0,sizeof(r)); memset(g,0,sizeof(g)); } void outfile(char ad[]){ FILE *fp; fp=fopen(ad,"wb"); printhead(_c,n,m); int ns=54; for(int i=n;i;i--){ for(int j=1;j<=m;j++){ _c[ns++]=b[i][j]; _c[ns++]=g[i][j]; _c[ns++]=r[i][j]; } int k=(3*m)%4; for(int i=0;i<k;i++) _c[ns++]=0; } fwrite(_c,1,ns,fp); fclose(fp); } void readfile(char ad[]){ FILE *fp; fp=fopen(ad,"rb"); fread(_c,1,MFLONG,fp); fclose(fp); for(int i=0x15;i>=0x12;i--) m=m<<8,m=m+_c[i]; for(int i=0x19;i>=0x16;i--) n=n<<8,n=n+_c[i]; int ns=54; for(int i=n;i;i--){ for(int j=1;j<=m;j++){ b[i][j]=_c[ns++]; g[i][j]=_c[ns++]; r[i][j]=_c[ns++]; } int k=(m*3)%4; ns+=k; } fclose(fp); } }; board S,P,P2,CAP; void capture(){ d(VK_SNAPSHOT); u(VK_SNAPSHOT); S.readfile("screenx.bmp"); } #define epsR 2 #define epsG 2 #define epsB 2 #define conY 1.4356 ///过滤底色和阴影的参数 #define LR 43 #define RR 68 #define LG 49 #define RG 57 #define LB 76 #define RB 102 #define tan30 0.5773 /*#define JumpepsR 7 #define JumpepsG 7 #define JumpepsB 7//用于判断目标点的东西*/ int JumpepsR,JumpepsG,JumpepsB; int wx[]={-1,-1,-1,0,1,1,1,0}; int wy[]={-1,0,1,1,1,0,-1,-1}; struct node{ int r,g,b; node(){r=g=b=0;} node(unsigned char R,unsigned char G,unsigned B){ r=R; g=G; b=B; } friend bool operator <(node a,node b){ if(a.r!=b.r) return a.r<b.r; if(a.g!=b.g) return a.g<b.g; return a.b<b.b; } bool cmp(int R,int G,int B){ int e1=abs(r-R); int e2=abs(g-G); int e3=abs(b-B); if(e1>epsR) return 0; if(e2>epsG) return 0; if(e3>epsB) return 0; return 1; } }; int pf(int x){return x*x;} map<node,int> mp,mmp; int chessX,chessY;//棋子的x,y坐标 int TX,TY; int lineR[10000]={0},lineG[10000]={0},lineB[10000]={0},X[10000]={0},Y[10000]={0}; int wave(){//完成对图像的底色和阴影过滤,以及求出棋子的中心点 P.clear(); int sx=32,ex=1074; int sy=682,ey=1265; P.m=ey-sy+1; P.n=ex-sx+1; for(int i=sx;i<=ex;i++) for(int j=sy;j<=ey;j++){ P.r[i-sx+1][j-sy+1]=S.r[i][j]; P.g[i-sx+1][j-sy+1]=S.g[i][j]; P.b[i-sx+1][j-sy+1]=S.b[i][j]; } // P.readfile("st720.bmp"); //抓出图像 P2=P; int sumx=0,sumy=0,cntx=0; for(int i=1;i<=P.n;i++) for(int j=1;j<=P.m;j++){ int dR=abs(P.r[i][j]); int dG=abs(P.g[i][j]); int dB=abs(P.b[i][j]); int cnt=0; if(LR<=dR&&dR<=RR) cnt++; if(LG<=dG&&dG<=RG) cnt++; if(LB<=dB&&dB<=RB) cnt++; if(cnt==3){ P.r[i][j]=P.g[i][j]=P.b[i][j]=100; sumx+=i; sumy+=j; cntx++; } }//识别棋子 for(int i=1;i<=P.n;i++){ mp.clear(); for(int j=1;j<=P.m;j++) mp[node(P.r[i][j],P.g[i][j],P.b[i][j])]++; map<node,int>::iterator it; node maxid,maxid2; int maxn=0; for(it=mp.begin();it!=mp.end();it++){ if(maxn<it->second){ maxn=it->second; maxid=it->first; } } maxid2.r=maxid.r/conY; maxid2.g=maxid.g/conY; maxid2.b=maxid.b/conY; for(int j=1;j<=P.m;j++){ if(maxid.cmp(P.r[i][j],P.g[i][j],P.b[i][j])) P.r[i][j]=P.g[i][j]=P.b[i][j]=0; if(maxid2.cmp(P.r[i][j],P.g[i][j],P.b[i][j])) P.r[i][j]=P.g[i][j]=P.b[i][j]=0; } } if(cntx==0) return 1; sumx/=cntx; sumy/=cntx; sumx+=14; P.r[sumx][sumy]=P.g[sumx][sumy]=P.b[sumx][sumy]=255; chessX=sumx+2; chessY=sumy; int cnt=0; // P.outfile("ok.bmp"); CAP.readfile("0000white.bmp");//对白点的特殊优化 int minn=1234567890,maxx=0,maxy=0; for(int j=chessX;j>=chessX-300;j--) for(int i=1;i<=P.m-CAP.m;i++){ int sum=0,pcnt=0; for(int ii=1;ii<CAP.m;ii++) for(int jj=1;jj<CAP.n;jj++){ sum+=pf(P.r[j+jj][i+ii]-CAP.r[jj][ii]); sum+=pf(P.g[j+jj][i+ii]-CAP.g[jj][ii]); sum+=pf(P.b[j+jj][i+ii]-CAP.b[jj][ii]); } if(sum==0){ minn=sum,maxx=i,maxy=j; break; } } //cout<<minn<<endl; if(minn==0){ printf("catch white point!\n"); for(int ii=1;ii<CAP.m;ii++) for(int jj=1;jj<CAP.n;jj++){ P.r[maxy+jj][maxx+ii]=0; P.g[maxy+jj][maxx+ii]=255; P.b[maxy+jj][maxx+ii]=0; } TX=maxy+6; TY=maxx+8; P.r[TX][TY]=255; P.g[TX][TY]=P.b[TX][TY]=0; // P.outfile("test.bmp"); return 2; } CAP.readfile("0000brown.bmp");//对437天的特殊优化 minn=1234567890,maxx=0,maxy=0; for(int j=chessX;j>=chessX-300;j--) for(int i=1;i<=P.m-CAP.m;i++){ int sum=0,pcnt=0; for(int ii=1;ii<CAP.m;ii++) for(int jj=1;jj<CAP.n;jj++){ sum+=pf(P.r[j+jj][i+ii]-CAP.r[jj][ii]); sum+=pf(P.g[j+jj][i+ii]-CAP.g[jj][ii]); sum+=pf(P.b[j+jj][i+ii]-CAP.b[jj][ii]); } if(sum==0){ minn=sum,maxx=i,maxy=j; break; } } //cout<<minn<<endl; if(minn==0){ printf("catch brown point!\n"); for(int ii=1;ii<CAP.m;ii++) for(int jj=1;jj<CAP.n;jj++){ P.r[maxy+jj][maxx+ii]=0; P.g[maxy+jj][maxx+ii]=255; P.b[maxy+jj][maxx+ii]=0; } TX=maxy+4; TY=maxx+6; P.r[TX][TY]=255; P.g[TX][TY]=P.b[TX][TY]=0; // P.outfile("test.bmp"); return 0; } //printf("%d %d\n",maxx,maxy); memset(X,0,sizeof(X)); memset(Y,0,sizeof(Y)); memset(lineR,0,sizeof(lineR)); memset(lineG,0,sizeof(lineG)); memset(lineB,0,sizeof(lineB)); //loop:; mp.clear(); if(chessY<=290 ){ for(int i=chessY+60;i<=P.m;i++){ int j=chessX-(i-chessY)*tan30; if(P.r[j][i]==0&&P.g[j][i]==0&&P.b[j][i]==0) continue; cnt++; lineR[cnt]=P.r[j][i]; lineG[cnt]=P.g[j][i]; lineB[cnt]=P.b[j][i]; X[cnt]=j; Y[cnt]=i; mp[node(P.r[j][i],P.g[j][i],P.b[j][i])]++; cnt++; lineR[cnt]=P.r[j-4][i]; lineG[cnt]=P.g[j-4][i]; lineB[cnt]=P.b[j-4][i]; X[cnt]=j-4; Y[cnt]=i; mp[node(P.r[j-4][i],P.g[j-4][i],P.b[j-4][i])]++; cnt++; lineR[cnt]=P.r[j+4][i]; lineG[cnt]=P.g[j+4][i]; lineB[cnt]=P.b[j+4][i]; X[cnt]=j+4; Y[cnt]=i; mp[node(P.r[j+4][i],P.g[j+4][i],P.b[j+4][i])]++; cnt++; lineR[cnt]=P.r[j+8][i]; lineG[cnt]=P.g[j+8][i]; lineB[cnt]=P.b[j+8][i]; X[cnt]=j+8; Y[cnt]=i; mp[node(P.r[j+8][i],P.g[j+8][i],P.b[j+8][i])]++; cnt++; lineR[cnt]=P.r[j-8][i]; lineG[cnt]=P.g[j-8][i]; lineB[cnt]=P.b[j-8][i]; X[cnt]=j-8; Y[cnt]=i; mp[node(P.r[j-8][i],P.g[j-8][i],P.b[j-8][i])]++; P.r[j+1][i]=P.r[j-1][i]=255; P.g[j+1][i]=P.g[j-1][i]=255; P.b[j+1][i]=P.b[j-1][i]=0; } }else{ for(int i=chessY-60;i;i--){ int j=chessX-(chessY-i)*tan30; if(P.r[j][i]==0&&P.g[j][i]==0&&P.b[j][i]==0) continue; cnt++; lineR[cnt]=P.r[j][i]; lineG[cnt]=P.g[j][i]; lineB[cnt]=P.b[j][i]; X[cnt]=j; Y[cnt]=i; mp[node(P.r[j][i],P.g[j][i],P.b[j][i])]++; cnt++; lineR[cnt]=P.r[j-4][i]; lineG[cnt]=P.g[j-4][i]; lineB[cnt]=P.b[j-4][i]; X[cnt]=j-4; Y[cnt]=i; mp[node(P.r[j-4][i],P.g[j-4][i],P.b[j-4][i])]++; cnt++; lineR[cnt]=P.r[j+4][i]; lineG[cnt]=P.g[j+4][i]; lineB[cnt]=P.b[j+4][i]; X[cnt]=j+4; Y[cnt]=i; cnt++; mp[node(P.r[j+4][i],P.g[j+4][i],P.b[j+4][i])]++; lineR[cnt]=P.r[j+8][i]; lineG[cnt]=P.g[j+8][i]; lineB[cnt]=P.b[j+8][i]; X[cnt]=j+8; Y[cnt]=i; cnt++; mp[node(P.r[j+8][i],P.g[j+8][i],P.b[j+8][i])]++; lineR[cnt]=P.r[j-8][i]; lineG[cnt]=P.g[j-8][i]; lineB[cnt]=P.b[j-8][i]; X[cnt]=j-8; Y[cnt]=i; mp[node(P.r[j-8][i],P.g[j-8][i],P.b[j-8][i])]++; P.r[j+1][i]=P.r[j-1][i]=255; P.g[j+1][i]=P.g[j-1][i]=255; P.b[j+1][i]=P.b[j-1][i]=0; } } //printf("colorsum:%d\n",mp.size()); if(mp.size()<40){ JumpepsR=JumpepsG=JumpepsB=1; }else if(mp.size()<100){ JumpepsR=JumpepsG=JumpepsB=4; }else if(mp.size()<400){ JumpepsR=JumpepsG=JumpepsB=7; }else JumpepsR=JumpepsG=JumpepsB=10; if(cnt==0) return 1; //if(cnt==0) goto loop; int maxn=0,maxid=0,quan=3; for(int i=1;i<=cnt;i++){ quan=3; int R=lineR[i]; int G=lineG[i]; int B=lineB[i]; int sum=0; for(int j=1;j<=cnt;j++){ int DeltaR=abs(lineR[j]-R); int DeltaG=abs(lineG[j]-G); int DeltaB=abs(lineB[j]-B); if(DeltaR>JumpepsR) continue; if(DeltaG>JumpepsG) continue; if(DeltaB>JumpepsB) continue; sum+=abs(X[j]-chessX)*0.05+4; } if(sum>maxn) maxn=sum,maxid=i; } int sumX=0,sumY=0,sum=0; int R=lineR[maxid]; int G=lineG[maxid]; int B=lineB[maxid]; for(int j=1;j<=cnt;j++){ int DeltaR=abs(lineR[j]-R); int DeltaG=abs(lineG[j]-G); int DeltaB=abs(lineB[j]-B); if(DeltaR>JumpepsR) continue; if(DeltaG>JumpepsG) continue; if(DeltaB>JumpepsB) continue; sum++; P.r[X[j]][Y[j]]=0; P.g[X[j]][Y[j]]=255; P.b[X[j]][Y[j]]=0; sumX+=X[j]; sumY+=Y[j]; } if(sum==0) return 1; sumX/=sum; sumY/=sum; //求出目标点坐标 P.r[sumX][sumY]=255; P.g[sumX][sumY]=P.b[sumX][sumY]=0; TX=sumX; TY=sumY; //P.outfile("test.bmp"); return 0; //点击模组 } int main(){ while(!gk(VK_F7)) s(10); keybd_event(VK_F7,0,2,0); char c[100]; int cas=0,x=0,y,sum=0,buchang=0; //Sleep(2000); int last=0; while(1){ cas++; capture(); Sleep(400); capture(); Sleep(200); int k=wave(); if(gk(VK_F7)) return 0; int X=abs(TX-chessX),Y=abs(TY-chessY); double d=0.866,b=1.732; int he=2*X+d*(Y-b*X); printf("dist=%d pixel\n",he); me(2); s(he*2.528); me(4); Sleep(1500); freopen("log.txt","r",stdin); scanf("%d%d",&x,&y); fclose(stdin); sprintf(c,"log%d.bmp",x); P.outfile(c); sprintf(c,"st%d.bmp",x); P2.outfile(c); x++; y+=(k==2); printf("sumjump=%d,centrejump=%d\n\n",x,y); freopen("log.txt","w",stdout); printf("%d %d\n",x,y); fclose(stdout); freopen("con","w",stdout); } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号