数据结构之图

一，什么是图

表示多对多的关系

图包含一组顶点和一组边（不考虑重边和自回路）

二，图的表示

邻接矩阵表示图：有边的表示1，无边的表示0

邻接矩阵优点：

1.  直观
2. 查找方便
3. 查询一个顶点的所有邻接点方便
4. 方便计算度（该顶点的边数），入度，出度（有向图需要查看行（出度）和列（入度））

邻接矩阵缺点：

1. 浪费空间：稀疏图（点很多而边很少）
2. 浪费时间：

邻接表：只存非零元素，不唯一，稀疏图

三，图的遍历

DFS(深度优先搜索，Depth First Search）: 原路返回=>树的先序遍历

BFS(广度优先搜索，Breath First Search)=>树的层次遍历

 

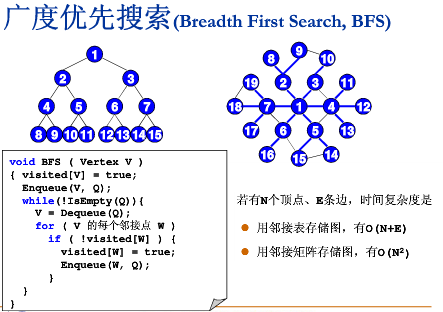
 连通：如果从v到w存在一条（无向）路径，则称v和w是连通的

 路径：v到w的路径是一系列的顶点的集合，其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数（如果带权，则是所有边的权重和）。如果v和w之间的所有顶点都不同，则称简单路径（无回路）

回路：起点等于终点的路径

连通图：图中任意两顶点均连通

连通分量：无向图中的极大连通子图

强连通；有向图中顶点v和w之间存在双向路径（既有从v->w又有从w->v，可以不是同一条），则称v和w是强连通

弱连通：去掉方向后的v和w是连通的

强连通图：有向图中任意两顶点均强连通

强连通分量：有向图的极大强连通子图

 

六度空间算法

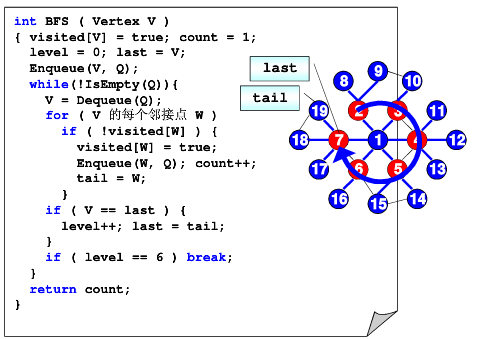
中序遍历和前序遍历直接求后序遍历 

 

 

完全二叉搜索树的核心代码

 

 

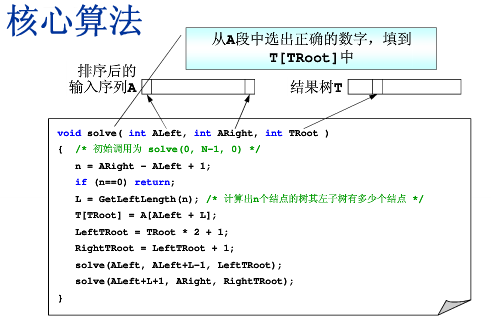
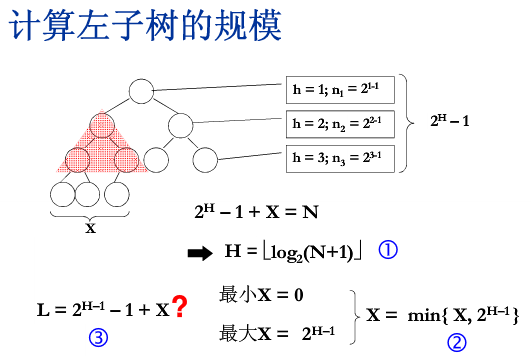
最短路径

网络：带权的图，

1. 单元最短路径：固定源点；
   1. （有向）无权图
      1. 递增顺序
   2. （有向）有权图
      1. 负值圈（不考虑）
      2. Dijkstra算法

         实现上述代码中红线伪代码的方法

2. 多元最短路径：任意两点
   1. 直接将单元最短路算法调用V遍
   2. Floyd算法

      1. 

         

          

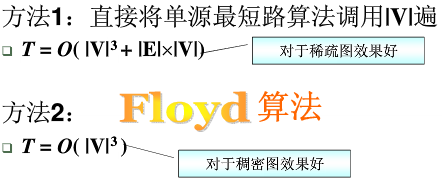
 最小生成树

定义：

 

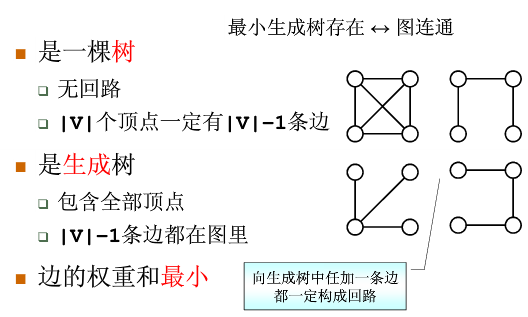
稠密图的贪心算法：Prim算法，从一个点一点一点向外扩张延伸，进入树内的点的dist都为0，往外延伸时是与树中任意一个结点距离最小

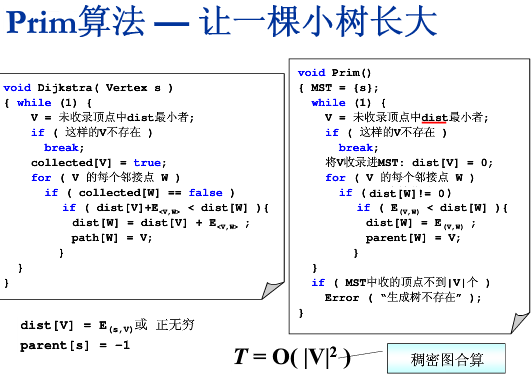
稀疏图的贪心算法：每次从剩余所有边中取最短的边，所选边不能构成回路

 

拓扑排序

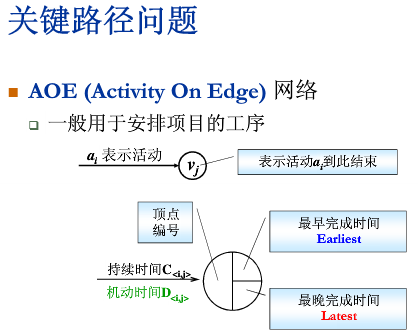
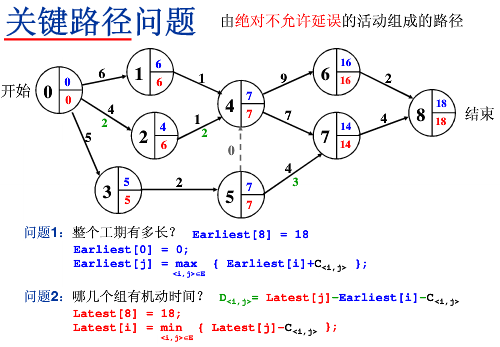
1. AOV(Activity On Vertex) 网络

 

 

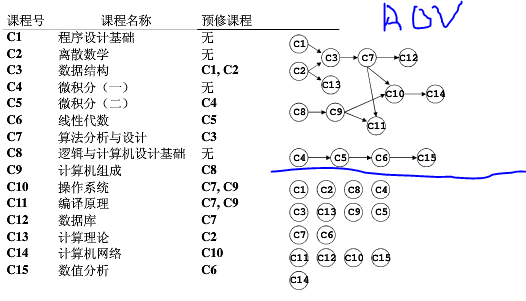
 算法部分：