数据结构之线性结构之堆栈

二，堆栈

 

中缀表达式：运算符位于两数之后； a+b*c-d/e

后缀表达式：运算符位于两数之后； abc*+de/-；计算机表示式求解时的读法；用堆栈实现计算

前缀表达式：运算符位于两数之前； -+a*bc/de

 

堆栈（操作受限制的线性表），先入后出，只在一端（栈顶，top)做插入和删除

push和pop为最常用的操作，可以交替进行；

栈的顺序存储实现：用数组实现堆栈

#define MAXSIZE 10
typedef struct {
    int Data[MAXSIZE];
    int Top;   //指向栈顶的位置
}Stack;

 

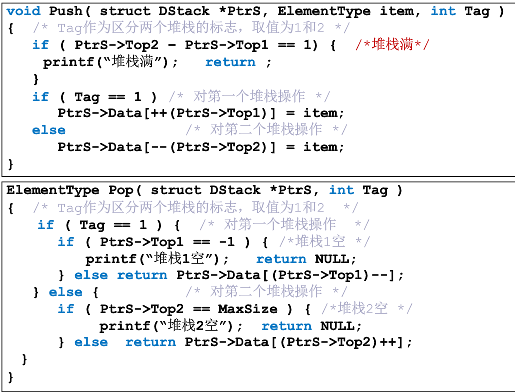
void Push(Stack *PtrS, int item)//item为待插入元素
{
    if (PtrS->Top == MAXSIZE)
    {
        printf("堆栈满"); 
        return;
    }
    else
    {
        PtrS->Data[++(PtrS->Top)] = item;//先把指向top的指针指向下一位，再往该位置插入数字
        return;
    }
}

 

int Pop(Stack *PtrS)
{
    if (PtrS->Top==-1)
    {
        printf("栈为空");
        return -NAN;   //此处只要是特殊值，标志错误
    }
    else
    {
        return(PtrS->Data[(PtrS->Top)--]);//返回栈顶的值之后需要把栈顶的指针的值往下移动一位
    }
}

 

一个数组实现两个堆栈：一个指向数组头，一个指向数组尾部，当两个指针相邻时，数组满，即两头向中间生长

堆栈的链式存储实现

用链表表示堆栈，链栈，实际是个单链表。插入和删除操作只能在链栈的栈顶进行。即栈顶Top应该在链表的头，不能在尾部（单向链表只能找到下一项，找不到上一项）

typedef struct NodeStack {
    int Data;
    struct NodeStack *Next;
}LinkStack;

void LinkPush(int item, LinkStack *S)
{
    LinkStack *temp = new LinkStack;
    temp->Data = item;
    temp->Next = S->Next;
    S->Next = temp;
}

int LinkPop(LinkStack *S)
{
    LinkStack *temp = new LinkStack;
    int result;
    if (S->Next == NULL)
    {
        printf("堆栈空");
        return NULL;
    }
    else
    {
        temp = S->Next;//删除某一个数时需要定位到该数之前的那个数
        S->Next = temp->Next;
        result = temp->Data;
        delete(temp);
        return result;
    }
}

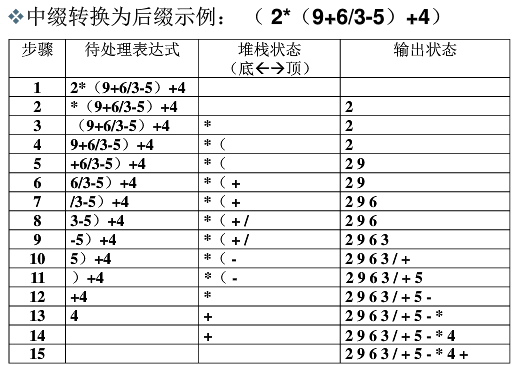
中缀表达式转换成后缀表达式：堆栈实现，复杂度为n

1. 运算数：直接输出；
2. 左括号：压栈
3. 右括号：输出栈顶元素，直到遇到左括号（出栈，不输出）
4. 运算符：大于栈顶，压栈；小于等于栈顶，输出栈顶，比较新栈顶，循环，压栈；括号内的运算符依旧遵循此规则
5. 堆栈存留一一输出

　　　　　　小于等于栈顶时，栈顶输出

 

后缀表达式可以用堆栈求出其具体数值：

把运算数压入栈中，遇到运算符，取出栈顶两元素运算后的结果压入栈中，继续

堆栈其他作用：

1. 函数调用及递归实现
2. 深度优先搜索
3. 回溯算法