博客作业05--查找
1.1查找的思维导图
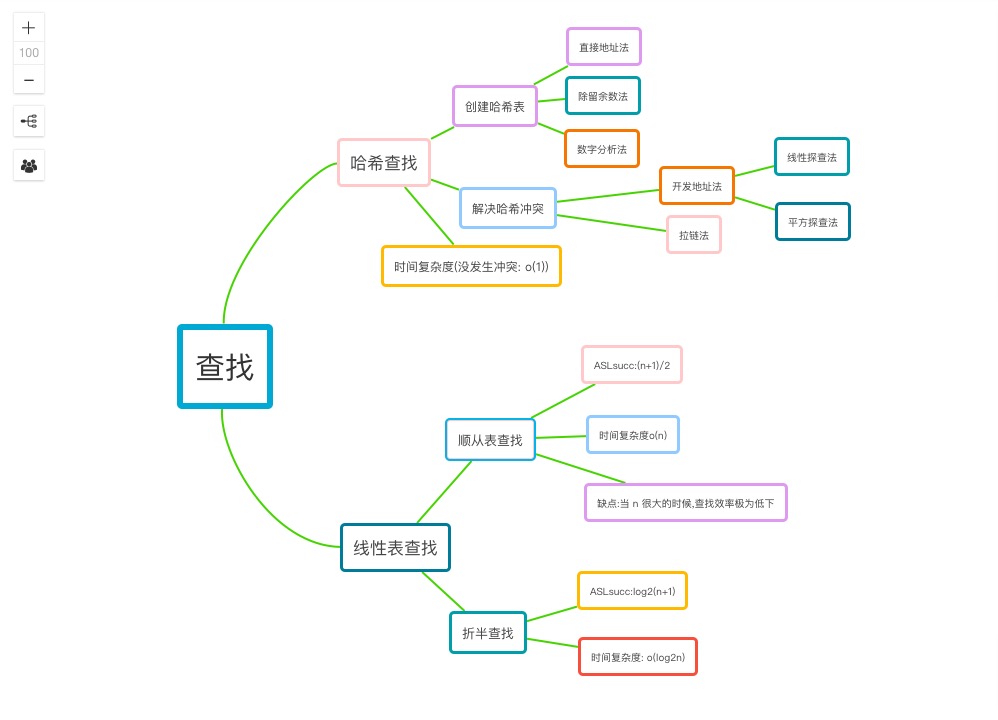
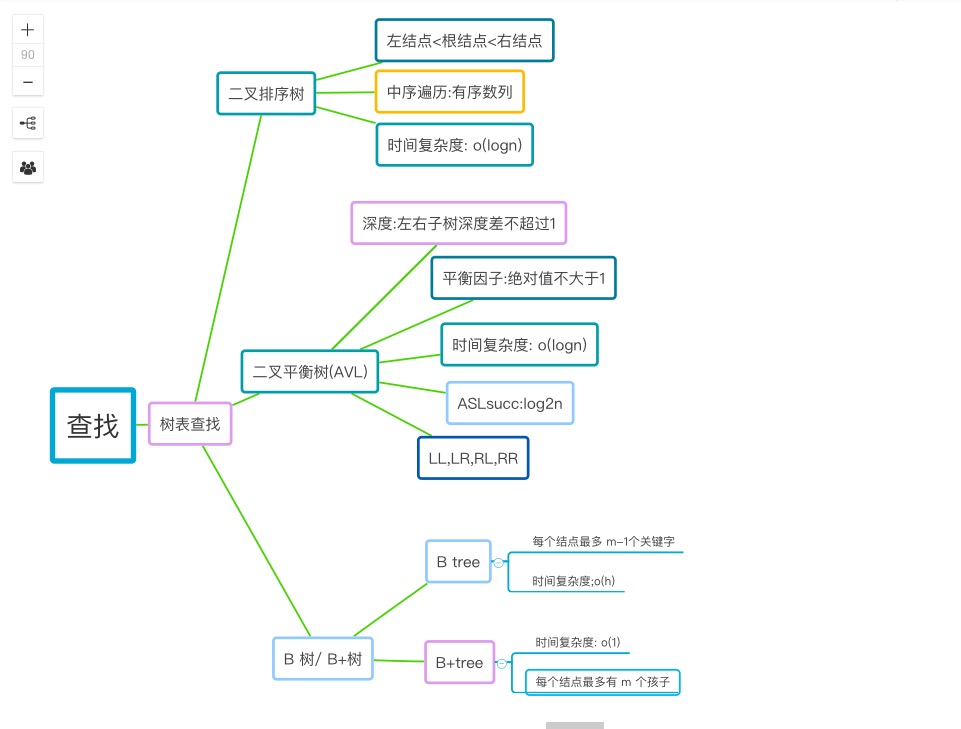
1.2 查找学习体会
在本章节中,查找的内容很多,同时计算平均查找度的方法也不同,时间复杂度也不同,由于内容比较多,故各种概念容易混淆,需要多花时间研究.
我们学习了线性表,数表,和哈希表的查找。并且学会了在相同数据结构下减少时间复杂度的方法和思想。
对应二叉搜索树的特点:
1.若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2.若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3.任意节点的左、右子树也分别为二叉查找树。
4.中序遍历得到递增序列.
2.PTA实验作业(4分)
2.1 题目1:是否二叉搜索树
2.2 设计思路(伪代码或流程图)
bool IsBST(BinTree T)
{
若树空则为二叉搜索树;
若左子树不为空且左子树最大值大于最大值
返回不是
若右子树不为空且右子树最小值小于最大值if (T->Right!=NULL && minValue(T->Right) <= T->Data)
返回不是
返回左子树和右子树
}
2.3 代码截图
2.4 PTA提交列表说明。

编译错误是因为PTA的编程环境和我用的DEV不一样,有些地方不能通用
部分正确是因为左右都是,但答案是NO这个情况我没有考虑
2.1 题目2:二叉搜索树中的最近公共祖先
2.2 设计思路(伪代码或流程图)
int find(Tree T,int u)
{
如果是空树返回0
如果查找不到u,v返0
如果u,v有一个是根节点返回根节点的关键字
如果u,v一个在左子树,一个在右子树返回根节点的关键字
如果都在右子树继续调用,节点变成右节点
如果都在左子树继续调用,节点变成左节点
2.3 代码截图
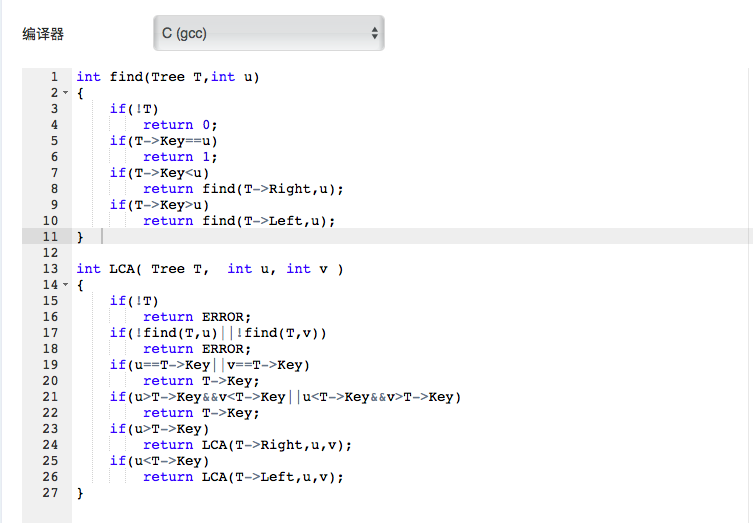
2.4 PTA提交列表说明。

这道较为简单,在 dev 上运行后即可
2.1 题目3:qq 账户的申请与登录
2.2 设计思路(伪代码或流程图)
struct UserNode{
int ID;
char password[20];
ptrUser next;
};
ptrUser HashTable[MAXN];
//定义用户结构体指针,包括密码和 id
void InsertUserNode(int idx,int id,char* pwd)
//插入用户 id 子函数
void NewUser(int id,char pwd[])
//新建用户子函数
void Login(int id,char pwd[])
//登录用户子函数
2.3 代码截图

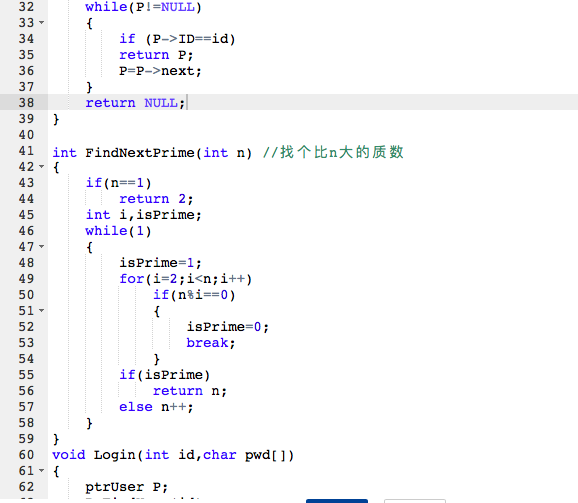

2.4 PTA提交列表说明。

map的不熟悉以及不会使用
3.截图本周题目集的PTA最后排名(3分)

第90名
共108分
3.1 PTA排名(截图带自己名字的排名)
2分
4. 阅读代码
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
红黑树的时间复杂度为: O(lgn)
将一个节点插入到红黑树中,需要执行哪些步骤
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
红黑树本身就是一颗二叉查找树,将节点插入后,该树仍然是一颗二叉查找树。也就意味着,树的键值仍然是有序的。此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。这也就意味着,任何的旋转和重新着色操作,都不会改变它仍然是一颗二叉查找树的事实。
好吧?那接下来,我们就来想方设法的旋转以及重新着色,使这颗树重新成为红黑树!
第二步:将插入的节点着色为"红色"。
为什么着色成红色,而不是黑色呢?为什么呢?在回答之前,我们需要重新温习一下红黑树的特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
将插入的节点着色为红色,不会违背"特性(5)"!少违背一条特性,就意味着我们需要处理的情况越少。接下来,就要努力的让这棵树满足其它性质即可;满足了的话,它就又是一颗红黑树了。o(∩∩)o...哈哈
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。




