二叉堆

二叉堆

 

 

我们知道堆栈是一种LIFO（后进先出）结构，队列是一种FIFO（先进先出）结构，而二叉堆是一种最小值先出的数据结构，因此二叉堆很适合用来做排序。

二叉堆的性质：二叉堆是一棵完全二叉树。

二叉堆采用数组来存储（按广度优先遍历的顺序），而没有像普通的树结构使用指针来表示节点间的关系。

如下图所示：

 

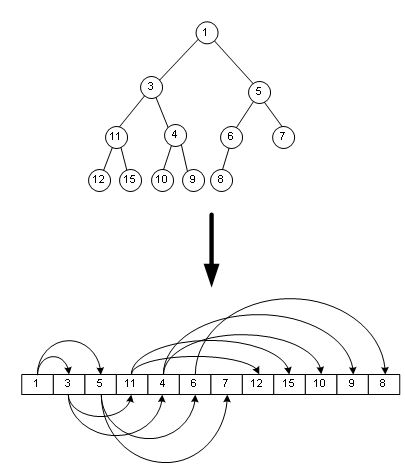
如图，最小的一个元素就是数组第一个元素。

将二叉堆按最广优先遍历的顺序编号从0到N-1，根据完全二叉树的性质，则第n个结点的子结点分别是2n+1和2n+2，其父结点是(n-1)/2。并且，叶子结点的下标是从 N/2开始，一直到N-1。这样，对于数组中的任意一个元素，我们可以很方便的计算出它的父节点、孩子节点所在的位置（即数组下标）。

 

如果下标是从1开始（算法导论就是从1开始），元素就是1,...,n，则第i个节点的子节点分别是2i和2i+1，其父节点是i/2.叶子节点的下标从n/2+1开始。

 

最小堆和最大堆

最大堆：父结点的键值总是大于或等于任何一个子结点的键值；最大堆常用于排序算法。
最小堆：父结点的键值总是小于或等于任何一个子结点的键值；最小堆常用于优先队列。

堆的意义就在于：最快的找到最大/最小值，在堆结构中插入一个值重新构造堆结构，取走最大/最下值后重新构造堆结构；其时间复杂度为O(logN)；

堆实践中用途不在于排序，其主要用在调度算法中，比如优先级调度，每次取优先级最高的，时间驱动，取时间最小/等待最长的 等等 ，分为最大堆/最小堆。

 

利用最大堆和最小堆可以求一个包含N个元素的数组的前K大（或小）的数，原理如下：

我们首先取这N个元素中的前K个元素来建立一个由K个元素组成的小（大）顶堆，这样堆顶元素便是当前已读取元素中的第K大（小）者；然后，依次读取剩下的N-K个元素，而对于其中的每个元素x，若x大于（小于）当前的堆顶元素，则将堆顶元素替换为x，并自堆顶至向下调整堆；这样，在读取完所有元素后，堆中的K个元素即为这N个数中的前K个最大（小）元素，同时堆顶元素为这N个数中的第K大（小）元素。

 

 

---

插入

如果要在二叉堆中插入或删除一个元素，必须保证堆性质仍能满足。

为了将x插入到堆中，我们在下一个可用位置创建一个空穴，如果x放在空穴中不破坏堆的序，那么插入完成。否则我们把父节点的元素移到空穴中，这样，空穴就上移一步了，继续操作直到可以将x放入空穴为之。。 这步骤叫上滤。

 

 

 

 

---

 

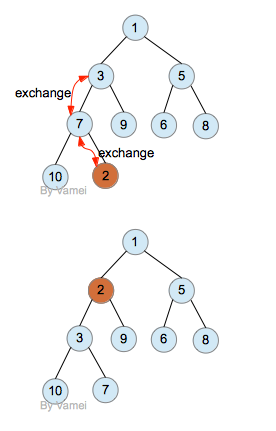
删除

删除操作一定是踢出数组的第一个元素（即根节点），这么来第一个元素以前的位置就成了空位，因此堆中最后一个元素x必须移到该堆的某个地方。我们将空穴的两个儿子中较小者移入空穴，这样空穴就下移了一步，重复步骤直到x可以放进去为止（比较x和孩子的大小）。这种策略叫做下滤。

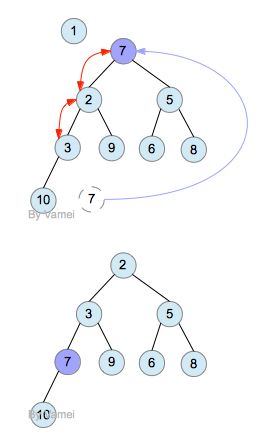
插入：这里数组从0-(n-1),

    /**
     * insert into the priority queue,maintaining heap order.
     * duplicates are allowed.
     * @param x the item to insert.
     * 这里以小根堆为例
     */
    public void insert(int x){
        //二叉堆的实现是数组以及一个代表长度的整数
        //判断长度是不是到数组最后了
        if(currentSize==array.length-1)
            enlargeArray(array.length*2+1);
        //上滤
        int hole=currentSize;//从0到n-1的下标。
        //hole-1)/2表示父节点
        while(x<array[(hole-1)/2]){
            array[hole]=array[(hole-1)/2];
            hole=(hole-1)/2;//空穴移到父节点。
        }
        array[hole]=x;
    }

 

删除：

 

    public int deleteMin(){
        int minItem=array[0];
        array[0]=array[currentSize-1];//将最后一个元素放到被删除的位置
        percolateDown(0);
        return minItem;
    }
    /**
     * 下滤
     * @param hole 是下滤开始的位置
     */
    private void percolateDown(int hole) {
        int child;//孩子中较小的孩子
        int tmp=array[hole];//要下滤的元素
        while(hole*2+1<=currentSize-1){
            child=hole*2+1;//左儿子位置
            //child不是最后一个节点（有右孩子），而且右孩子比左孩子小，那么child为较小的那个孩子
            if(child!=currentSize-1&&array[child+1]<array[child])
                child++;
            if(array[child]<tmp){
                array[hole]=array[child]; 
                    //孩子上移，空穴就下滤了。
                hole=child;
            }
            else
                break;
        }
        
        array[hole]=tmp;
        
    }                

 

构建堆：因为是数组，所以只要重排数组元素就行。将所有父节点下滤就行。

public void buildHeap(int[] nums){
    //先将nums数组的元素拷贝到堆数组array中，此步省略
    for(int i=currentSize/2-1;i>=0;i--){
        percolateDown(i);
    }
}

 

参考：https://www.cnblogs.com/chenny7/p/4108954.html

参考：《数据结构与算法分析java语言描述》