机器学习---核函数

前言：当我跟你说起核的时候，你的脑海里一定是这样的：

想到的一定是BOOMBOOM。谈核色变，但是今天我们说的核却温和可爱的多了。

我记得我前面说到了SVM的核武器是核函数，这篇文章可以作为http://www.cnblogs.com/xiaohuahua108/p/5934282.html这篇文章的下篇。但是我这里首先强调一下，核函数不是仅仅在SVM里使用，他只是一个工具，把低维数据映射到高维数据的工具。

形如这样：

本来是二维的数据，现在我们把它映射的高维。这里也需要说明下，低维到高维，维数没有一个数量上的标准，可能就是无限维到无限维。

一 核

1.1 核的介绍

内核方法是一类用于模式分析或识别的算法，其最知名的使用是在支持向量机（SVM）。模式分析的一般任务是在一般类型的数据（例如序列，文本文档，点集，向量，图像等）中找到并研究一般类型的关系（例如聚类，排名，主成分，相关性，分类）图表等）。内核方法将数据映射到更高维的空间，希望在这个更高维的空间中，数据可以变得更容易分离或更好的结构化。对这种映射的形式也没有约束，这甚至可能导致无限维空间。然而，这种映射函数几乎不需要计算的，所以可以说成是在低维空间计算高维空间内积的一个工具。

1.2 核的诀窍

内核技巧是一个非常有趣和强大的工具。 它是强大的，因为它提供了一个从线性到非线性的连接以及任何可以只表示两个向量之间的点积的算法。 它来自如下事实：如果我们首先将我们的输入数据映射到更高维的空间，那么我在这个高维的空间进行操作出的效果，在原来那个空间就表现为非线性。

现在，内核技巧非常有趣，因为不需要计算映射。 如果我们的算法只能根据两个向量之间的内积表示，我们所需要的就是用一些其他合适的空间替换这个内积。 这就是"技巧"的地方：无论使用怎样的点积，它都被内核函数替代。 核函数表示特征空间中的内积，通常表示为：

 

K（x，y）= <φ（x），φ（y）>

 

使用内核函数，该算法然后可以被携带到更高维空间中，而不将输入点显式映射到该空间中。 这是非常可取的，因为有时我们的高维特征空间甚至可以是无限维，因此不可能计算。

讲了这么大一段废话，还是我上文的加黑部分，在低维中计算高维数据的点积。

1.3 核函数的性质

核函数必须是连续的，对称的，并且最优选地应该具有正（半）定Gram矩阵。据说满足Mercer定理的核是正半定数，意味着它们的核矩阵只有非负特征值。使用肯定的内核确保优化问题将是凸的和解决方案将是唯一的。

然而，许多并非严格定义的核函数在实践中表现得很好。一个例子是Sigmoid内核，尽管它广泛使用，但它对于其参数的某些值不是正半定的。 Boughorbel（2005）也实验证明，只有条件正定的内核在某些应用中可能胜过大多数经典内核。

内核还可以分为各向异性静止，各向同性静止，紧凑支撑，局部静止，非稳定或可分离非平稳。此外，内核也可以标记为scale-invariant（规模不变）或scale-dependent（规模依赖），这是一个有趣的属性，因为尺度不变内核驱动训练过程不变的数据的缩放。

 

补充：Mercer 定理：任何半正定的函数都可以作为核函数。所谓半正定的函数f(x_i,x_j)，是指拥有训练数据集合（x₁,x₂,...x_n)，我们定义一个矩阵的元素a_ij = f(x_i,x_j)，这个矩阵式n*n的，如果这个矩阵是半正定的，那么f(x_i,x_j)就称为半正定的函数。这个mercer定理不是核函数必要条件，只是一个充分条件，即还有不满足mercer定理的函数也可以是核函数

1.4 如何选择核

我导师说是世界性难题，反正我不懂，如果有懂得，可以私聊我哦。

但是据说高斯核效果很好。

二 几种常用的核

2.1 线性核

线性内核是最简单的内核函数。 它由内积<x，y>加上可选的常数c给出。 使用线性内核的内核算法通常等于它们的非内核对应物，即具有线性内核的KPCA与标准PCA相同。

 

表达式 ：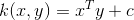

2.2 多项式核函数

多项式核是非固定内核。 多项式内核非常适合于所有训练数据都归一化的问题。我记得一般都会把问题归一化吧？？

表达式：k（x，y）=（αx ^ T y + c）^ d

可调参数是斜率α，常数项c和多项式度d。

2.3 高斯核

高斯核是径向基函数核的一个例子。

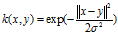
或者，它也可以使用来实现

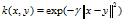
可调参数sigma在内核的性能中起着主要作用，并且应该仔细地调整到手头的问题。 如果过高估计，指数将几乎呈线性，高维投影将开始失去其非线性功率。 另一方面，如果低估，该函数将缺乏正则化，并且决策边界将对训练数据中的噪声高度敏感。

 

2.4指数的内核

指数核与高斯核密切相关，只有正态的平方被忽略。 它也是一个径向基函数内核。

表达式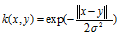：。和高斯核确实很像，哈哈。

2.5 拉普拉斯算子核

拉普拉斯核心完全等同于指数内核，除了对sigma参数的变化不那么敏感。 作为等价的，它也是一个径向基函数内核。

 

表达式：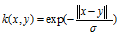

重要的是注意，关于高斯内核的σ参数的观察也适用于指数和拉普拉斯内核。

 

好了今天就讲到这里，下次有时间在来和大家分享其他的核函数吧。。。如果感觉我写的还可以，麻烦点个粉，或者点一个推荐哦。