java 根据二叉树前序 ，中序求后续

在一棵二叉树总，前序遍历结果为：ABDGCEFH，中序遍历结果为：DGBAECHF，求后序遍历结果。

我们知道：

前序遍历方式为：根节点->左子树->右子树

中序遍历方式为：左子树->根节点->右子树

后序遍历方式为：左子树->右子树->根节点

从这里可以看出，前序遍历的第一个值就是根节点，然后再中序遍历中找到这个值，那么这个值的左边部分即为当前二叉树的左子树部分前序遍历结果，这个值的右边部分即为当前二叉树的右子树部分前序遍历结果。因此，通过这个分析，可以恢复这棵二叉树，得到这样的一段伪码：

 

节点 getRoot(前序，中序)

c=前序第一个字符

pos=c在中序中的位置

len1=中序pos左半部分长度

len2=中序pos右半部分长度

新建节点r，令r的元素等于c

r的左儿子=getRoot(前序位置1开始的len1长度部分，中序pos位置的左半部分)

r的右儿子=getRoot(前序位置len1开始右半部分，中序pos位置的右半部分)

return r

 

如图1示：

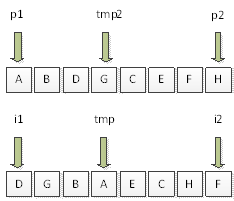
图1

输入前序ABDGCEFH，中序DGBAECHF，可以得出

A为该二叉树的根节点

1: BDG为该二叉树左子树的前序

2: DGB为该二叉树左子树的中序

根据1和2可以构建一棵左子树

 

3: CEFH为该二叉树右子树的前序

4: ECHF为该二叉树右子树的中序

根据3和4可以构建一个右子树

 

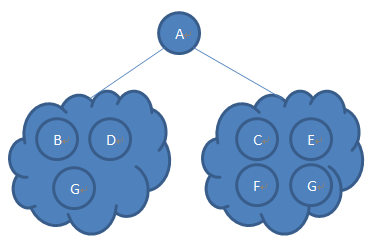
执行至该步骤的时候就得到了该二叉树的云结构，如图2所示，A为根节点，BDG在它的左子树上，CEFG在它的右子树上。

如此递归即可以构建一棵完整的二叉树

 

java代码

class DataNode{
    int data;
    DataNode leftChild = null;
    DataNode rightChild = null;
}

public class NodeTree {
    
    DataNode rootNode;
    DataNode tempNode;
    //int index_root; 
    DataNode left_childDataNode;
    DataNode right_childDataNode;
    
    public DataNode initRootNode(int[] preArray){
        rootNode = new DataNode();
        rootNode.data = preArray[0];
        return rootNode;
    }
    
    public  void BuildTree(int[] preArray,int[] midArray,DataNode rootNode){
        int index_root = getIndex(midArray, rootNode.data);
        int lengthOfRightTree = preArray.length - index_root -1;
        
        int[] preArray_left;
        int[] preArray_right;
        int[] midArray_left;
        int[] midArray_right;
        
        if (index_root>0) {
            left_childDataNode = new DataNode();
            if (index_root==1) {
                left_childDataNode.data = midArray[0];
                rootNode.leftChild = left_childDataNode;
            }else {
                preArray_left = new int[index_root];
                midArray_left = new int[index_root];
                System.arraycopy(preArray, 1, preArray_left, 0, index_root);
                System.arraycopy(midArray, 0, midArray_left, 0, index_root);
                left_childDataNode.data = preArray_left[0];
                rootNode.leftChild = left_childDataNode;
                BuildTree(preArray_left, midArray_left, left_childDataNode);
            }    
        }
        
        if (lengthOfRightTree>0) {
            right_childDataNode = new DataNode();
            if (lengthOfRightTree==1) {
                right_childDataNode.data = midArray[index_root+1];
                rootNode.rightChild = right_childDataNode;
                return;
            }else {
                preArray_right  = new int[lengthOfRightTree];
                midArray_right = new int[lengthOfRightTree];
                System.arraycopy(preArray, index_root+1, preArray_right, 0,lengthOfRightTree);
                System.arraycopy(midArray, index_root+1, midArray_right, 0, lengthOfRightTree);
                right_childDataNode.data = preArray_right[0];
                rootNode.rightChild = right_childDataNode;
                BuildTree(preArray_right, midArray_right,right_childDataNode);
            }
        }
    }
    
    public int getIndex(int[] array,int temp){
        int index = -1;
        for (int i = 0; i < array.length; i++) {
            if (array[i]==temp) {
                index = i;
                return index;
            }
        }
        return index;
    }
    //后序遍历
    public void postOrderTraverse(DataNode node){
        if (node==null) {
            return;
        }
        postOrderTraverse(node.leftChild);
        postOrderTraverse(node.rightChild);
        System.out.print(node.data);
    }
    //前序遍历
    public void preOrderTraverse(DataNode node){
        if (node==null) {
            return;
        }
        System.out.print(node.data);
        preOrderTraverse(node.leftChild);
        preOrderTraverse(node.rightChild);
    }
    //中序遍历
    public void inOrderTraverse(DataNode node){
        if (node==null) {
            return;
        }
        inOrderTraverse(node.leftChild);
        System.out.print(node.data);
        inOrderTraverse(node.rightChild);
    }
    
    public static void main(String args[]){
        int[] preArray = {1,2,3};
        int[] midArray = {1,2,3};
        NodeTree tree = new NodeTree();
        DataNode headNode = tree.initRootNode(preArray);
        tree.BuildTree(preArray, midArray, headNode);
        tree.postOrderTraverse(headNode);
    }
    
}