ccf 201803-4 棋局评估 (对抗搜索)
问题描述
Alice和Bob正在玩井字棋游戏。
井字棋游戏的规则很简单:两人轮流往3*3的棋盘中放棋子,Alice放的是“X”,Bob放的是“O”,Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时,游戏结束,该种棋子的持有者获胜。当棋盘被填满的时候,游戏结束,双方平手。
Alice设计了一种对棋局评分的方法:
- 对于Alice已经获胜的局面,评估得分为(棋盘上的空格子数+1);
- 对于Bob已经获胜的局面,评估得分为 -(棋盘上的空格子数+1);
- 对于平局的局面,评估得分为0;
井字棋游戏的规则很简单:两人轮流往3*3的棋盘中放棋子,Alice放的是“X”,Bob放的是“O”,Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时,游戏结束,该种棋子的持有者获胜。当棋盘被填满的时候,游戏结束,双方平手。
Alice设计了一种对棋局评分的方法:
- 对于Alice已经获胜的局面,评估得分为(棋盘上的空格子数+1);
- 对于Bob已经获胜的局面,评估得分为 -(棋盘上的空格子数+1);
- 对于平局的局面,评估得分为0;
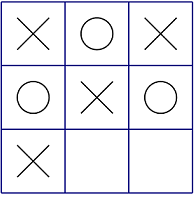
例如上图中的局面,Alice已经获胜,同时棋盘上有2个空格,所以局面得分为2+1=3。
由于Alice并不喜欢计算,所以他请教擅长编程的你,如果两人都以最优策略行棋,那么当前局面的最终得分会是多少?
由于Alice并不喜欢计算,所以他请教擅长编程的你,如果两人都以最优策略行棋,那么当前局面的最终得分会是多少?
输入格式
输入的第一行包含一个正整数T,表示数据的组数。
每组数据输入有3行,每行有3个整数,用空格分隔,分别表示棋盘每个格子的状态。0表示格子为空,1表示格子中为“X”,2表示格子中为“O”。保证不会出现其他状态。
保证输入的局面合法。(即保证输入的局面可以通过行棋到达,且保证没有双方同时获胜的情况)
保证输入的局面轮到Alice行棋。
每组数据输入有3行,每行有3个整数,用空格分隔,分别表示棋盘每个格子的状态。0表示格子为空,1表示格子中为“X”,2表示格子中为“O”。保证不会出现其他状态。
保证输入的局面合法。(即保证输入的局面可以通过行棋到达,且保证没有双方同时获胜的情况)
保证输入的局面轮到Alice行棋。
输出格式
对于每组数据,输出一行一个整数,表示当前局面的得分。
样例输入
3
1 2 1
2 1 2
0 0 0
2 1 1
0 2 1
0 0 2
0 0 0
0 0 0
0 0 0
1 2 1
2 1 2
0 0 0
2 1 1
0 2 1
0 0 2
0 0 0
0 0 0
0 0 0
样例输出
3
-4
0
-4
0
样例说明
第一组数据:
Alice将棋子放在左下角(或右下角)后,可以到达问题描述中的局面,得分为3。
3为Alice行棋后能到达的局面中得分的最大值。
第二组数据:
Bob已经获胜(如图),此局面得分为-(3+1)=-4。 第三组数据: 井字棋中若双方都采用最优策略,游戏平局,最终得分为0。 数据规模和约定 对于所有评测用例,1 ≤ T ≤ 5。
#include <iostream> #include <algorithm> using namespace std; int a[3][3]; //判断行是否胜利 ,at为第几行,id为是谁在下棋,1为Alice,2为Bob bool row(int at,int id) { if(a[at][0] == id && a[at][1] == id && a[at][2] == id) { return true; } return false; } //判断列是否胜利 ,at为第几行,id为是谁在下棋,1为Alice,2为Bob bool line(int at,int id) { if(a[0][at] == id && a[1][at] == id && a[2][at] == id) { return true; } return false; } //如果胜利计算当前棋盘的得分 int sum(int id) { int s = 1; for(int i=0;i<3;i++) { for(int j=0;j<3;j++) { if(a[i][j] == 0) { s++; } } } //Alice胜利,得分为正 if(id == 1) { return s; } else { return -1 * s; } } void show() { for(int i=0;i<3;i++) { for(int j = 0;j<3;j++) { cout << a[i][j] << " "; } cout << endl; } cout << endl; } //判断是否获胜 bool win(int id) { bool yes = false; //先比较当前局面的行 for(int i=0;i<3;i++) { if(row(i,id) == true) { yes = true; } } //再比较当前局面的列 for(int i=0;i<3;i++) { if(line(i,id) == true) { yes = true; } } //比较对角线 if(a[0][0] == id && a[1][1] == id && a[2][2] == id) { yes = true; } if(a[0][2] == id && a[1][1] == id && a[2][0] == id) { yes = true; } //判断是否胜利 if(yes) { return true; } else { return false; } } //对抗搜索,每个人都取对自己最有利的得分 int dfs(int id) { //无路可走,和棋 if(sum(id) == 1 || sum(id) == -1) { return 0; } //max表示 alice能得的最高分 int maxNum = -1000; //min表示bob能得到的最高分 int minNum = 1000; //遍历所有情况 //并判断当前局面,用当前最大值与对手回合的最大值进行比较 for(int i=0;i<3;i++) { for(int j=0;j<3;j++) { if(a[i][j] == 0) { //当前棋手在a[i][j]落子 ,再对此时的局面进行判断 a[i][j] = id; if( win(id) ) { int score = sum(id); a[i][j] = 0; //score>0表明Alice获胜,返回Alice的得分 //score<0表明Bob获胜,返回Bod的得分 return score > 0 ? max(maxNum,score) : min(minNum,score); } //每个人都假设自己能赢,用自己的最高分和对手的下一次进攻最高分比相比较, //对手能赢返回正,不能赢返回0 //如果判断此种局面赢不了,则会返回一个负值 if(id == 1) { maxNum = max(maxNum,dfs( id%2 + 1)); } else { minNum = min(minNum,dfs( id%2 + 1)); } //回溯 a[i][j] = 0; } } } return id==1 ? maxNum : minNum; } int main() { int n; cin >> n; for(int i=0;i<n;i++) { for(int j=0;j<3;j++) { for(int k=0;k<3;k++) { cin >> a[j][k]; } } if(win(1)) { cout << sum(1) << endl; continue; } if(win(2)) { cout << sum(2) << endl; continue; } int res = dfs(1); cout << res << endl; } return 0; }


