【原创】递归算法的要素总结

8个月没维护过blog了，想想看也是经历了挺多的，学了不少东西。慢慢的把自己的一些心得和总结发出来，和大家分享和改正。

好了，上面是题外话，今天的主题是递归算法的实现要素和分析。

 

一、分析和总结

 

写好一个递归算法，我认为主要是把握好如下三个方面：

1. 提取重复的逻辑。

2. 控制逻辑边界。

3. 恰当的退出。

 

1. 重复逻辑

出现重复逻辑一定是必不可少的，因为递归的精髓就是loop。但是，重复的逻辑需要抽象。抽象出来一个干净利落的可循环逻辑对程序编写的帮助很大。下面将会提到一个例子，有更多分析。

2. 控制逻辑边界

控制边界保证了程序在正确的框架下运行。因为抽象出来的逻辑需要一个框架保证其可以递归执行，“刚刚好”是它的要点。写程序也经常因为边界把控的不准确容易留下bug。

那么如何正确控制边界？一个比较好的办法，就是对边界也进行逻辑上的递归。因为递归是层层相同，那么第一层和第k层是一致的。第一层容易得出执行边界，那么相应的可以抽象第k层的执行边界。不过第k层的边界是逻辑上的，而第一层通常是数值上的。通常在第一层的辅助下抽象出严格的逻辑边界。

3. 合适退出递归

递归的退出往往和逻辑边界是相辅相成的，这一点下面的例子也会提到。

一般递归的退出有两种表现形式：

1.下层递归检测边界溢出退出。

特点是在递归代码的开始，会有边界控制。

2.本层递归检查边界。

特点是在进入下层递归前检查边界。

这两种方式最大的不同在于效率，因为每层递归会有对临时数据的保存，所以减少递归层数可以降低程序损耗。

 

三者关系：

2和3的根本在于1的抽象逻辑，一个好的递归不仅思想上干净利落，并且在代码表现上也是简单直接。

可以从下面的同一道题的两份代码中体会。

 

二、代码分析

这是leetcode上面的一道题，是根据中序和后序遍历的结果来恢复二叉树。

下面有两份代码，第一份算是正例，1、2、3点的结合比较到位。第二份算是侧例，帮助大家体会和理解1、2、3点的不同导致代码层面的差异。

代码如下：

/**
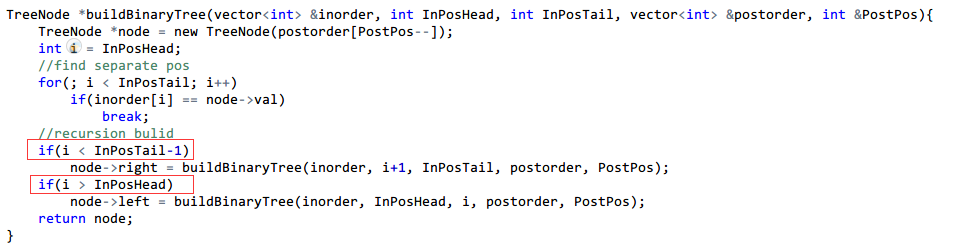
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {
        if(inorder.size() == 0)
            return NULL;
        int PostPos = postorder.size()-1;
        return buildBinaryTree(inorder, 0, inorder.size(), postorder, PostPos);
    }
    
    TreeNode *buildBinaryTree(vector<int> &inorder, int InPosHead, int InPosTail, 
　　　　　　　　　　　　　　　　　　　　vector<int> &postorder, int &PostPos){
        TreeNode *node = new TreeNode(postorder[PostPos--]);
        int i = InPosHead;
        //find separate pos
        for(; i < InPosTail; i++)
            if(inorder[i] == node->val)
                break;
        //recursion bulid
        if(i < InPosTail-1)
            node->right = buildBinaryTree(inorder, i+1, InPosTail, postorder, PostPos);
        if(i > InPosHead)
            node->left = buildBinaryTree(inorder, InPosHead, i, postorder, PostPos);
        return node;
    }
};

算法的思路是：根据后序排列来确定对应中序的根节点(1)，然后构建右子树和左子树(2)。 (括号的数字代表上面的三个方面)

分析：

这句话中 ”构建右左子树“表明了可以通过递归逻辑实现，并确定了边界的抽象(2)。而”根据后序排列来确定对应中序的根节点“是对递归逻辑的抽象(1)。

可以看到，我在上面两句话中都刻意强调了”右左子树“，而不是”左右子树“，这是因为后序表的逆向排列正好代表了右树优先的根节点，所以先建右子树再创建左子树是简单直接的方法。这对2的边界控制很有帮助。(恰当的抽象)

并且逻辑退出(3)放到了同层递归检测，这不仅减少程序消耗而且显示表明了结束条件，对可读性也有帮助。

 

再贴一份代码，这个递归的抽象逻辑和我写的稍有不同(我的是优先构建右子树，这份是不分左右顺序)，但是在边界控制稍显复杂(后序表的边界控制)。具体的分析留给大家了。

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    private int postPos;
    
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(inorder == null)
            return null;
        HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
        for(int i=0; i<inorder.length; i++)
            map.put(inorder[i], i);
        return helper(inorder, 0, inorder.length-1, postorder, 0, postorder.length-1, map);
    }
    
    private TreeNode helper(int[] inorder, int inL, int inR,
                            int[] postorder, int postL, int postR, HashMap<Integer, Integer> map){
        if(inL > inR)
            return null;
        TreeNode root = new TreeNode(postorder[postR]);
        int index = map.get(root.val);
        root.left  = helper(inorder, inL, index-1, postorder, postL, postL+index-inL-1, map);
    root.right = helper(inorder, index+1, inR, postorder, postL+index-inL, postR-1, map);
        return root;
    }
}

 

最后，虽然递归有逻辑简单，代码清晰的优点，但是并不建议首先考虑用递归解决问题。好的程序还是需要通过深入解析写出更快捷、更巧妙的算法，而不是把问题交给机器暴力解决。当然递归加剪枝可以避开一些不必要的搜索，不过大部分还是有替代的办法。

希望能帮初学者对递归有个认识和理解，加深对计算机解题方式的理解。

 

转载请注明出处，谢谢~  http://www.cnblogs.com/xiaoboCSer/p/4172741.html