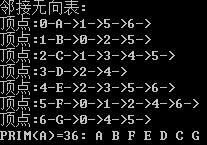
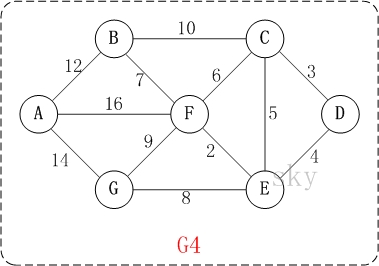
数据结构之最小生成树Prim算法
普里姆算法介绍
普里姆(Prim)算法,是用来求加权连通图的最小生成树算法
基本思想:对于图G而言,V是所有顶点的集合;现在,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。 从所有uЄU,vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边。
代码实现
1. 思想逻辑
(1)以无向图的某个顶点(A)出发,计算所有点到该点的权重值,若无连接取最大权重值#define INF (~(0x1<<31))
(2)找到与该顶点最小权重值的顶点(B),再以B为顶点计算所有点到改点的权重值,依次更新之前的权重值,注意权重值为0或小于当前权重值的不更新,因为1是一当找到最小权重值的顶点时,将权重值设为了0,2是会出现无连接的情况。
(3)将上述过程一次循环,并得到最小生成树。
2. Prim算法
// Prim最小生成树 void Prim(int nStart) { int i = 0; int nIndex=0; // prim最小树的索引,即prims数组的索引 char cPrims[MAX]; // prim最小树的结果数组 int weights[MAX]; // 顶点间边的权值 cPrims[nIndex++] = m_mVexs[nStart].data; // 初始化"顶点的权值数组", // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。 for (i = 0; i < m_nVexNum; i++) { weights[i] = GetWeight(nStart, i); } for (i = 0; i < m_nVexNum; i ++) { if (nStart == i) { continue; } int min = INF; int nMinWeightIndex = 0; for (int k = 0; k < m_nVexNum; k ++) { if (weights[k]!= 0 && weights[k] < min) { min = weights[k]; nMinWeightIndex = k; } } // 找到下一个最小权重值索引 cPrims[nIndex++] = m_mVexs[nMinWeightIndex].data; // 以找到的顶点更新其他点到该点的权重值 weights[nMinWeightIndex]=0; int nNewWeight = 0; for (int ii = 0; ii < m_nVexNum; ii++) { nNewWeight = GetWeight(nMinWeightIndex, ii); // 该位置需要特别注意 if (0 != weights[ii] && weights[ii] > nNewWeight) { weights[ii] = nNewWeight; } } } // 计算最小生成树的权重值 int nSum = 0; for (i = 1; i < nIndex; i ++) { int min = INF; int nVexsIndex = GetVIndex(cPrims[i]); for (int kk = 0; kk < i; kk ++) { int nNextVexsIndex = GetVIndex(cPrims[kk]); int nWeight = GetWeight(nVexsIndex, nNextVexsIndex); if (nWeight < min) { min = nWeight; } } nSum += min; } // 打印最小生成树 cout << "PRIM(" << m_mVexs[nStart].data <<")=" << nSum << ": "; for (i = 0; i < nIndex; i++) cout << cPrims[i] << " "; cout << endl; }
3. 全部实现

#include "stdio.h" #include <iostream> using namespace std; #define MAX 100 #define INF (~(0x1<<31)) // 最大值(即0X7FFFFFFF) class EData { public: EData(char start, char end, int weight) : nStart(start), nEnd(end), nWeight(weight){} char nStart; char nEnd; int nWeight; }; // 边 struct ENode { int nVindex; // 该边所指的顶点的位置 int nWeight; // 边的权重 ENode *pNext; // 指向下一个边的指针 }; struct VNode { char data; // 顶点信息 ENode *pFirstEdge; // 指向第一条依附该顶点的边 }; // 无向邻接表 class listUDG { public: listUDG(){}; listUDG(char *vexs, int vlen, EData **pEData, int elen) { m_nVexNum = vlen; m_nEdgNum = elen; // 初始化"邻接表"的顶点 for (int i = 0; i < vlen; i ++) { m_mVexs[i].data = vexs[i]; m_mVexs[i].pFirstEdge = NULL; } char c1,c2; int p1,p2; ENode *node1, *node2; // 初始化"邻接表"的边 for (int j = 0; j < elen; j ++) { // 读取边的起始顶点和结束顶点 c1 = pEData[j]->nStart; c2 = pEData[j]->nEnd; p1 = GetVIndex(c1); p2 = GetVIndex(c2); node1 = new ENode(); node1->nVindex = p2; node1->nWeight = pEData[j]->nWeight; if (m_mVexs[p1].pFirstEdge == NULL) { m_mVexs[p1].pFirstEdge = node1; } else { LinkLast(m_mVexs[p1].pFirstEdge, node1); } node2 = new ENode(); node2->nVindex = p1; node2->nWeight = pEData[j]->nWeight; if (m_mVexs[p2].pFirstEdge == NULL) { m_mVexs[p2].pFirstEdge = node2; } else { LinkLast(m_mVexs[p2].pFirstEdge, node2); } } } ~listUDG() { ENode *pENode = NULL; ENode *pTemp = NULL; for (int i = 0; i < m_nVexNum; i ++) { pENode = m_mVexs[i].pFirstEdge; if (pENode != NULL) { pTemp = pENode; pENode = pENode->pNext; delete pTemp; } delete pENode; } } void PrintUDG() { ENode *pTempNode = NULL; cout << "邻接无向表:" << endl; for (int i = 0; i < m_nVexNum; i ++) { cout << "顶点:" << GetVIndex(m_mVexs[i].data)<< "-" << m_mVexs[i].data<< "->"; pTempNode = m_mVexs[i].pFirstEdge; while (pTempNode) { cout <<pTempNode->nVindex << "->"; pTempNode = pTempNode->pNext; } cout << endl; } } // Prim最小生成树 void Prim(int nStart) { int i = 0; int nIndex=0; // prim最小树的索引,即prims数组的索引 char cPrims[MAX]; // prim最小树的结果数组 int weights[MAX]; // 顶点间边的权值 cPrims[nIndex++] = m_mVexs[nStart].data; // 初始化"顶点的权值数组", // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。 for (i = 0; i < m_nVexNum; i++) { weights[i] = GetWeight(nStart, i); } for (i = 0; i < m_nVexNum; i ++) { if (nStart == i) { continue; } int min = INF; int nMinWeightIndex = 0; for (int k = 0; k < m_nVexNum; k ++) { if (weights[k]!= 0 && weights[k] < min) { min = weights[k]; nMinWeightIndex = k; } } // 找到下一个最小权重值索引 cPrims[nIndex++] = m_mVexs[nMinWeightIndex].data; // 以找到的顶点更新其他点到该点的权重值 weights[nMinWeightIndex]=0; int nNewWeight = 0; for (int ii = 0; ii < m_nVexNum; ii++) { nNewWeight = GetWeight(nMinWeightIndex, ii); // 该位置需要特别注意 if (0 != weights[ii] && weights[ii] > nNewWeight) { weights[ii] = nNewWeight; } } } // 计算最小生成树的权重值 int nSum = 0; for (i = 1; i < nIndex; i ++) { int min = INF; int nVexsIndex = GetVIndex(cPrims[i]); for (int kk = 0; kk < i; kk ++) { int nNextVexsIndex = GetVIndex(cPrims[kk]); int nWeight = GetWeight(nVexsIndex, nNextVexsIndex); if (nWeight < min) { min = nWeight; } } nSum += min; } // 打印最小生成树 cout << "PRIM(" << m_mVexs[nStart].data <<")=" << nSum << ": "; for (i = 0; i < nIndex; i++) cout << cPrims[i] << " "; cout << endl; } private: // 获取<start, end>的权值,若start和end不是连接的,则返回无穷大 int GetWeight(int start, int end) { if (start == end) { return 0; } ENode *pTempNode = m_mVexs[start].pFirstEdge; while (pTempNode) { if (end == pTempNode->nVindex) { return pTempNode->nWeight; } pTempNode = pTempNode->pNext; } return INF; } // 返回顶点的索引 int GetVIndex(char ch) { int i = 0; for (; i < m_nVexNum; i ++) { if (m_mVexs[i].data == ch) { return i; } } return -1; } void LinkLast(ENode *pFirstNode, ENode *pNode) { if (pFirstNode == NULL || pNode == NULL) { return; } ENode *pTempNode = pFirstNode; while (pTempNode->pNext != NULL) { pTempNode = pTempNode->pNext; } pTempNode->pNext = pNode; } private: int m_nVexNum; // 顶点数目 int m_nEdgNum; // 边数目 VNode m_mVexs[MAX]; VNode m_PrimVexs[MAX]; }; void main() { char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; // 边 EData *edges[] = { // 起点 终点 权 new EData('A', 'B', 12), new EData('A', 'F', 16), new EData('A', 'G', 14), new EData('B', 'C', 10), new EData('B', 'F', 7), new EData('C', 'D', 3), new EData('C', 'E', 5), new EData('C', 'F', 6), new EData('D', 'E', 4), new EData('E', 'F', 2), new EData('E', 'G', 8), new EData('F', 'G', 9) }; int vlen = sizeof(vexs)/sizeof(vexs[0]); int elen = sizeof(edges)/sizeof(edges[0]); listUDG* pG = new listUDG(vexs, vlen, edges, elen); pG->PrintUDG(); // 打印图 pG->Prim(0); for (int i = 0; i < elen; i ++) { delete edges[i]; } return; }