2018冬令营模拟测试赛(一)
2018冬令营模拟测试赛(一)
[Problem A]全面战争不可避
试题描述

补充说明:铁路毁坏指的是这条铁路彻底消失了,不会对之后的询问造成影响(即询问之间是独立的)
输入

输出

输入示例1
5 4 4
1 2
1 3
2 4
2 5
1 2
2 4
3 4
1 4
输出示例1
1
2
1
1
输入示例2 & 输出示例2
数据规模及约定

题解
它保证每时每刻都是棵树,那么一条边贡献为 \(-1\),那么只需要数一下区间内出现了多少个不同的点就好了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 500010
int n, m, q, A[maxn<<1], pre[maxn<<1], lst[maxn];
int C[maxn<<1];
void update(int x) {
for(; x <= (m << 1); x += x & -x) C[x]++;
return ;
}
int sum(int x) {
int sum = 0;
for(; x; x -= x & -x) sum += C[x];
return sum;
}
struct Que {
int ql, qr, id;
Que() {}
Que(int _1, int _2, int _3): ql(_1), qr(_2), id(_3) {}
bool operator < (const Que& t) const { return ql < t.ql; }
} qs[maxn];
int Ans[maxn];
struct Num {
int lst, pos;
Num() {}
Num(int _, int __): lst(_), pos(__) {}
bool operator < (const Num& t) const { return lst < t.lst; }
} ns[maxn<<1];
int num[50], cntn;
void writeint(int x) {
if(!x) return (void)putchar('0');
cntn = 0;
while(x) num[cntn++] = x % 10, x /= 10;
dwn(i, cntn - 1, 0) putchar(num[i] + '0');
return ;
}
int main() {
n = read(); m = read(); q = read();
rep(i, 1, m) A[(i<<1)-1] = read(), A[i<<1] = read();
rep(i, 1, m << 1) ns[i] = Num(lst[A[i]], i), lst[A[i]] = i;
rep(kase, 1, q) {
int ql = read(), qr = read();
qs[kase] = Que(ql, qr, kase);
}
sort(qs + 1, qs + q + 1); sort(ns + 1, ns + (m << 1 | 1));
int j = 1;
rep(i, 1, q) {
while(j <= (m << 1) && ns[j].lst < (qs[i].ql << 1) - 1) update(ns[j++].pos);
Ans[qs[i].id] = sum(qs[i].qr << 1) - sum((qs[i].ql << 1) - 2) - (qs[i].qr - qs[i].ql + 1);
}
rep(i, 1, q) printf("%d\n", Ans[i]);
return 0;
}
[Problem B]神社闭店之日
试题描述

输入

输出

输入示例1
4 3 3 5
1 2 6 3
1 1
2 2
2 3
2 4
3 4
输出示例1
9
15
15
9
33
输入示例2 & 输出示例2
数据规模及约定

注意:数据范围发生改动,所有 \(b_i\) 的最小公倍数现在小于等于 \(10^{13}\)。
题解
首先用一下 KMP 中 border 的理论,不难发现满足要求的串必须是一个周期串,每个最小周期的长度就是所有 \(b_i(i \in [L_j, R_j])\) 和串长的最大公约数;于是现在有了一个暴力,令 \(G = \mathrm{gcd}\{b_i | i \in [L_j, R_j]\}\),则题目就是让求 \(\sum_{l=1}^L C^{\mathrm{gcd}(G, l)}\)。
这样只能过 \(60\) 分,考虑优化,显然是枚举 \(\mathrm{gcd}\) 然后用莫比乌斯反演。
\begin{equation}
\sum_{l=1}^L C^{\mathrm{gcd}(G, l)} \\
= \sum_{g|G} { c^g \sum_{g|l, l \in [1, L]} {[\mathrm{gcd}(G, l) = g]} } \\
= \sum_{g|G} { c^g \sum_{l=1}^{\lfloor \frac{L}{g} \rfloor} {[\mathrm{gcd}(\frac{G}{g}, l) = 1]} } \\
= \sum_{g|G} { c^g \sum_{l=1}^{\lfloor \frac{L}{g} \rfloor} { \sum_{d|\frac{G}{g}, d|l} {\mu(d)} } } \\
= \sum_{g|G} { c^g \sum_{d|\frac{G}{g}} { \mu(d) \sum_{d|l, l \in [1, \lfloor \frac{L}{g} \rfloor]} {1} } } \\
= \sum_{g|G} { c^g \sum_{gd|G} { \mu(d) \lfloor \frac{L}{gd} \rfloor } } \\
\notag
\end{equation}
此时,令 \(T = gd\),我们看看能不能消掉一个字母。注意这时 \(g|T\)。
\begin{equation}
= \sum_{g|G} { c^g \sum_{T|G, g|T} { \mu(\frac{T}{g}) \lfloor \frac{L}{T} \rfloor } } \\
= \sum_{T|G} { \lfloor \frac{L}{T} \rfloor \sum_{g|T} {c^g \mu(\frac{T}{g})} } \\
\notag
\end{equation}
其实字母个数并没有改变(去掉了一个 \(d\),但引入了 \(T\)),但是我们可以改变运算顺序了。可以发现,我们将枚举 \(T\) 放到了外层,这样后面那个 \(\sum_{g|T} {c^g \mu(\frac{T}{g})}\) 就只与 \(T\) 有关了,那么对于每一种可能的 \(T\),我们暴力枚举它的约数 \(g\),然后算出这个式子的值就好了。
可以发现后面询问出现的所有约数都是 \(\mathrm{lcm} \{ b_i | i \in [1, N] \}\) 的所有约数的真子集,所以我们预处理一下,再用个哈希,就可以 \(O(1)\) 询问了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
#define LL long long
LL read() {
LL x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 100010
#define MOD 998244353
int n, L, C, q;
LL A[maxn];
LL gcd(LL a, LL b) { return b ? gcd(b, a % b) : a; }
LL G[maxn<<2];
void build(int o, int l, int r) {
if(l == r) G[o] = A[l];
else {
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
build(lc, l, mid); build(rc, mid + 1, r);
G[o] = gcd(G[lc], G[rc]);
}
return ;
}
LL query(int o, int l, int r, int ql, int qr) {
if(ql <= l && r <= qr) return G[o];
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
LL ans = 0;
if(ql <= mid) ans = gcd(ans, query(lc, l, mid, ql, qr));
if(qr > mid) ans = gcd(ans, query(rc, mid + 1, r, ql, qr));
return ans;
}
const int HMOD = 1000037, MAXN = 11010;
struct Hash {
int ToT, head[HMOD], nxt[maxn], val[maxn];
LL key[maxn];
Hash(): ToT(0) { memset(head, 0, sizeof(head)); }
int Find(LL x) {
int u = x % HMOD;
for(int e = head[u]; e; e = nxt[e]) if(key[e] == x) return val[e];
return -1;
}
void Insert(LL x, int v) {
if(Find(x) >= 0) return ;
int u = x % HMOD;
key[++ToT] = x; val[ToT] = v; nxt[ToT] = head[u]; head[u] = ToT;
return ;
}
} cp, mu, Ans;
int Pow(int a, LL b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
int getmu(LL x) {
int cur = 1, cnt, m = (int)sqrt(x + .5);
rep(i, 2, m) if(x % i == 0) {
cnt = 0;
while(x % i == 0) {
if(++cnt > 1) return 0;
x /= i;
}
cur = -cur;
if(x == 1) break;
}
if(x > 1) cur = -cur;
return cur;
}
int f[MAXN], cd;
LL divs[MAXN];
void init(LL x) {
int m = (int)sqrt(x + .5);
rep(i, 1, m) if(x % i == 0) {
divs[++cd] = i;
if(i != x / i) divs[++cd] = x / i;
}
sort(divs + 1, divs + cd + 1);
rep(i, 1, cd) cp.Insert(divs[i], Pow(C, divs[i])), mu.Insert(divs[i], getmu(divs[i]));
rep(i, 1, cd) {
int s = 0;
rep(j, 1, i) if(divs[i] % divs[j] == 0) {
f[i] += (MOD + mu.Find(divs[i] / divs[j]) * cp.Find(divs[j])) % MOD;
if(f[i] >= MOD) f[i] -= MOD;
s += (LL)f[j] * (L / divs[j]) % MOD;
if(s >= MOD) s -= MOD;
}
Ans.Insert(divs[i], s);
}
return ;
}
int main() {
n = read(); L = read(); C = read(); q = read();
LL lcm = 1;
rep(i, 1, n) A[i] = read(), lcm = lcm / gcd(lcm, A[i]) * A[i];
build(1, 1, n);
init(lcm);
while(q--) {
int ql = read(), qr = read();
printf("%d\n", Ans.Find(query(1, 1, n, ql, qr)));
}
return 0;
}
[Problem C]唯一神
试题描述


输入

输出

输入示例1
2 2 2 0 1 2
输出示例1
300736801
输入示例2 & 输出示例2
数据规模及约定


题解
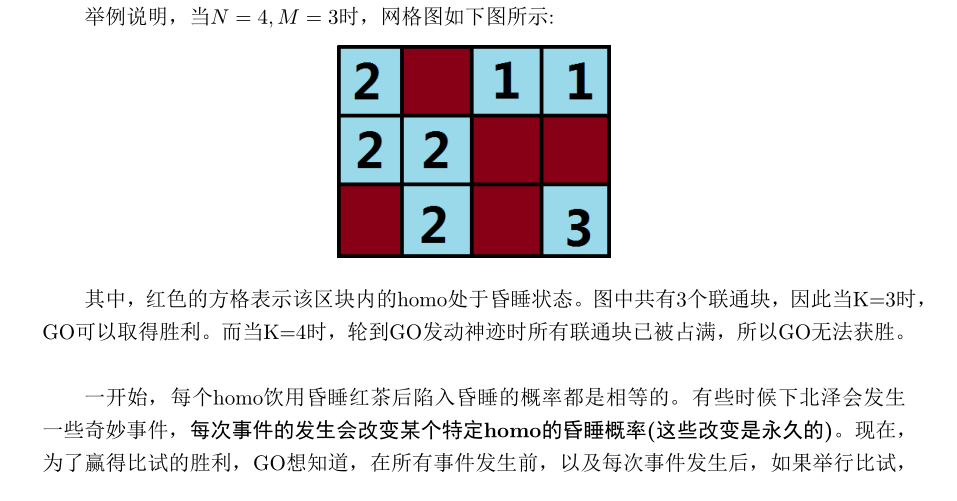
首先不难想到一个 dp,设 \(f(i, s, k)\) 表示对于前 \(i\) 行,第 \(i\) 行的连通状态为 \(s\)(这个连通状态最多有 \(9\) 种),当前连通块个数模 \(K\) 等于 \(k\) 时的概率。那么你可以预处理一下每两个连通性之间转移对答案的贡献,以及连通块的变化数量。
但是这样会发现每次修改都不得不重新 dp,非常费时。
考虑优化,我们发现每一步的转移都是类似的,即从 \(f(i, s, k)\) 转移到 \(f(i+1, s', k + \Delta k)\)(默认 \(k\) 这一维任何运算都在模 \(K\) 意义下),这样的话相当于乘上一个 \((maxs \cdot K) \times (maxs \cdot K)\)(\(maxs\) 为状态数)的矩阵,于是我们可以用线段树维护这样一个矩阵,每次修改只需要改 \(\mathrm{log} n\) 个矩阵。但是这样做无论是时间还是空间都不够。
考虑进一步优化,由于每次 \(k\) 转移到下一步非常有规律,是循环位移了 \(\Delta k\) 个位置,我们就可以想到这是一个多项式循环卷积的形式。
补充一下循环卷积的定义(形式)和做法:
定义:令 \(f(x) = \sum_{i=0}^{K-1} {a_i x^i}\) 和 \(g(x) = \sum_{i=0}^{K-1} {b_i x^i}\) 为两个 \(K-1\) 次多项式,那么它们的循环卷积 \((f \times g)(x) = \sum_{k=0}^{K-1} { x^k \sum_{i+j \equiv k (\mathrm{mod}\ K)} {a_i b_j} }\)。
做法:循环卷积就是在 DFT 的时候开 \(K\) 位,点值直接对应位相乘,然后再保持 \(K\) 位并 IDFT 回来,得到的系数向量就是循环卷积之后的结果了。
由于转化成点值之后,每一步点值都是对应位相乘,所以 \(K\) 个点值之间互相独立,所以对于每个状态我们维护一下这个点值,再线段树中对于每个点值维护一个 \(maxs \times maxs\) 的矩阵,那么 dp 的过程就是将最初的状态转化成点值,\(F_k\) 是一个 \(maxs\) 维的向量,向量第 \(i\) 维存储连通状态为 \(i\) 时的第 \(k\) 维点值。那个转移矩阵可以这样构造:将每一次转移看成乘上一个 \(p \cdot x^{\Delta k}\) 的多项式(\(p\) 是系数,等于该转移贡献的概率),然后将这个多项式转化成点值表达,转移矩阵上对应位置填上对应维度的点值就好了。最后在把最终状态的多项式转化回系数向量即可,答案就是 \(k = 0\) 那一维。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <map>
#include <vector>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 200010
#define maxs 10
#define maxk 10
#define maxnode 400000
#define MOD 370137601
#define G 37
#define LL long long
int n, m, K, q, p0, q0;
map <vector <int>, int> id;
vector <int> sta[maxs];
int cnts;
void search(vector <int> now) {
if(id.count(now)) return ;
sta[id[now] = ++cnts] = now;
rep(i, 0, m - 1)
rep(j, i + 1, m - 1) if(now[i] && now[j] && now[i] != now[j]) {
vector <int> to = now;
int c = min(to[i], to[j]);
rep(k, 0, m - 1) if(to[k] == to[i] || to[k] == to[j]) to[k] = c;
search(to);
}
return ;
}
int sleep[maxn][3], getup[maxn][3], fa[10], trans[maxs][maxs], tpow[maxs][maxs];
bool change[maxn][3];
int findset(int x) { return x == fa[x] ? x : fa[x] = findset(fa[x]); }
void getTrans() {
vector <int> A(m), B(m);
rep(sid, 1, cnts) {
A = sta[sid];
int cn = 0, id1[3], id2[3], cA = 0;
memset(id1, 0, sizeof(id1));
rep(i, 0, m - 1) if(A[i]) id1[i] = ++cn, cA = max(cA, A[i]);
rep(s, 0, (1 << m) - 1) {
int cnt = cn;
memset(id2, 0, sizeof(id2));
rep(i, 0, m - 1) if(s >> i & 1) id2[i] = ++cnt;
rep(i, 1, cnt) fa[i] = i;
rep(i, 0, m - 1) rep(j, i + 1, m - 1) if(A[i] == A[j] && A[i]) {
int u = findset(id1[i]), v = findset(id1[j]);
if(u != v) fa[v] = u;
}
rep(i, 0, m - 1) if(s >> i & 1) {
if(A[i]) {
int u = findset(id1[i]), v = findset(id2[i]);
if(u != v) fa[v] = u;
}
if(i && (s >> i - 1 & 1)) {
int u = findset(id2[i-1]), v = findset(id2[i]);
if(u != v) fa[v] = u;
}
}
int c = 0, cB = 0, num[10]; memset(num, 0, sizeof(num));
rep(i, 0, m - 1) if(s >> i & 1) {
int u = findset(id2[i]);
if(!num[u]) num[u] = ++c;
}
rep(i, 1, cnt) if(findset(i) == i) cB++;
rep(i, 0, m - 1) if(s >> i & 1) B[i] = num[findset(id2[i])]; else B[i] = 0;
trans[sid][s] = id[B]; tpow[sid][s] = (cB - cA + K) % K;
}
}
return ;
}
int Pow(int a, int b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
int Mat[maxk][maxk], _Mat[maxk][maxk], wk;
void FFT_init() {
wk = Pow(G, (MOD - 1) / K);
rep(i, 0, K - 1) rep(j, 0, K - 1) Mat[i][j] = Pow(wk, i * j), _Mat[i][j] = Pow(Mat[i][j], MOD - 2);
return ;
}
LL buf[maxs];
void FFT(int *A, int tp) {
memset(buf, 0, sizeof(buf));
rep(i, 0, K - 1) {
int *M = tp > 0 ? Mat[i] : _Mat[i];
rep(j, 0, K - 1) buf[i] += (LL)*(M + j) * A[j] % MOD;
}
if(tp < 0) rep(i, 0, K - 1) buf[i] = buf[i] % MOD * Pow(K, MOD - 2);
rep(i, 0, K - 1) A[i] = buf[i] % MOD;
return ;
}
struct Matrix {
int A[maxs][maxs];
Matrix() {}
Matrix operator * (const Matrix& t) const {
Matrix ans;
rep(i, 1, cnts) {
memset(buf, 0, sizeof(buf));
const int *mA = A[i];
rep(k, 1, cnts) {
const int *tA = t.A[k];
LL tmp = *(mA + k);
rep(j, 1, cnts) buf[j] += tmp * *(tA + j) % MOD;
}
rep(j, 1, cnts) ans.A[i][j] = buf[j] % MOD;
}
return ans;
}
} Pool[maxnode], Now[maxk];
int Arr[maxk], F[maxs][maxk];
int ToT;
struct SegTree {
int node[maxn<<2];
void build(int o, int l, int r, int level) {
node[o] = level;
if(l == r) return ;
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
build(lc, l, mid, level - 1); build(rc, mid + 1, r, level - 1);
return ;
}
void modify(int o, int l, int r, int x, int nid) {
if(l == r) Pool[node[o] = ++ToT] = Now[nid];
else {
int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
if(x <= mid) modify(lc, l, mid, x, nid); else modify(rc, mid + 1, r, x, nid);
Pool[node[o] = ++ToT] = Pool[node[lc]] * Pool[node[rc]];
}
return ;
}
} sgt[maxk];
int main() {
n = read(); m = read(); K = read(); q = read(); p0 = read(); q0 = read();
vector <int> A(m);
rep(i, 0, (1 << m) - 1) {
int c = 0;
rep(j, 0, m - 1)
if(i >> j & 1) {
if(j && (i >> j - 1 & 1)) A[j] = c;
else A[j] = ++c;
}
else A[j] = 0;
search(A);
}
getTrans();
FFT_init();
int _sleep = (LL)p0 * Pow(q0, MOD - 2) % MOD, _getup = (LL)(q0 - p0) * Pow(q0, MOD - 2) % MOD, clog;
for(clog = 1; (1 << clog) <= n; clog++); clog--;
ToT = K * (clog + 1);
rep(s, 1, cnts) {
rep(tr, 0, (1 << m) - 1) {
int t = trans[s][tr], p = 1;
rep(j, 0, m - 1) if(tr >> j & 1) p = (LL)p * _getup % MOD; else p = (LL)p * _sleep % MOD;
memset(Arr, 0, sizeof(Arr));
Arr[tpow[s][tr]] = p;
FFT(Arr, 1);
rep(i, 0, K - 1) Pool[i*(clog+1)+1].A[s][t] = Arr[i];
}
}
rep(i, 0, K - 1) {
rep(j, 1, clog) Pool[i*(clog+1)+j+1] = Pool[i*(clog+1)+j] * Pool[i*(clog+1)+j];
sgt[i].build(1, 1, n, (i + 1) * (clog + 1));
}
F[1][0] = 1;
FFT(F[1], 1);
// F[1~cnts][k] * Pool[sgt[k].node[1]]
LL tB[maxs];
rep(k, 0, K - 1) {
memset(tB, 0, sizeof(tB));
rep(i, 1, cnts) {
int *pA = Pool[sgt[k].node[1]].A[i];
rep(j, 1, cnts)
tB[j] += (LL)F[i][k] * *(pA + j) % MOD;
}
rep(i, 1, cnts) F[i][k] = tB[i] % MOD;
}
int ans = 0;
rep(i, 1, cnts) {
FFT(F[i], -1);
ans += F[i][0];
if(ans >= MOD) ans -= MOD;
}
printf("%d\n", ans);
while(q--) {
int x = read(), y = read() - 1, p1 = read(), q1 = read();
change[x][y] = 1;
sleep[x][y] = (LL)p1 * Pow(q1, MOD - 2) % MOD; getup[x][y] = (LL)(q1 - p1) * Pow(q1, MOD - 2) % MOD;
rep(s, 1, cnts) {
rep(tr, 0, (1 << m) - 1) {
int t = trans[s][tr], p = 1;
rep(j, 0, m - 1)
if(tr >> j & 1) p = (LL)p * (change[x][j] ? getup[x][j] : (LL)(q0 - p0) * Pow(q0, MOD - 2) % MOD) % MOD;
else p = (LL)p * (change[x][j] ? sleep[x][j] : (LL)p0 * Pow(q0, MOD - 2) % MOD) % MOD;
memset(Arr, 0, sizeof(Arr));
Arr[tpow[s][tr]] = p;
FFT(Arr, 1);
rep(i, 0, K - 1) Now[i].A[s][t] = Arr[i];
}
}
rep(i, 0, K - 1) sgt[i].modify(1, 1, n, x, i);
memset(F, 0, sizeof(F));
F[1][0] = 1;
FFT(F[1], 1);
// F[1~cnts][k] * Pool[sgt[k].node[1]]
rep(k, 0, K - 1) {
memset(tB, 0, sizeof(tB));
rep(i, 1, cnts) {
int *pA = Pool[sgt[k].node[1]].A[i];
rep(j, 1, cnts)
tB[j] += (LL)F[i][k] * *(pA + j) % MOD;
}
rep(i, 1, cnts) F[i][k] = tB[i] % MOD;
}
ans = 0;
rep(i, 1, cnts) {
FFT(F[i], -1);
ans += F[i][0];
if(ans >= MOD) ans -= MOD;
}
printf("%d\n", ans);
}
return 0;
}
又是一道常数卡得生活不能自理的题



 浙公网安备 33010602011771号
浙公网安备 33010602011771号