BZOJ3924 [Zjoi2015]幻想乡战略游戏

Description

 傲娇少女幽香正在玩一个非常有趣的战略类游戏，本来这个游戏的地图其实还不算太大，幽香还能管得过来，但是不知道为什么现在的网游厂商把游戏的地图越做越大，以至于幽香一眼根本看不过来，更别说和别人打仗了。 在打仗之前，幽香现在面临一个非常基本的管理问题需要解决。 整个地图是一个树结构，一共有n块空地，这些空地被n-1条带权边连接起来，使得每两个点之间有一条唯一的路径将它们连接起来。在游戏中，幽香可能在空地上增加或者减少一些军队。同时，幽香可以在一个空地上放置一个补给站。 如果补给站在点u上，并且空地v上有dv个单位的军队，那么幽香每天就要花费dv×dist(u,v)的金钱来补给这些军队。由于幽香需要补给所有的军队，因此幽香总共就要花费为Sigma(Dv*dist(u，v),其中1<=V<=N)的代价。其中dist(u,v)表示u个v在树上的距离（唯一路径的权和）。 因为游戏的规定，幽香只能选择一个空地作为补给站。在游戏的过程中，幽香可能会在某些空地上制造一些军队，也可能会减少某些空地上的军队，进行了这样的操作以后，出于经济上的考虑，幽香往往可以移动他的补给站从而省一些钱。但是由于这个游戏的地图是在太大了，幽香无法轻易的进行最优的安排，你能帮帮她吗？ 你可以假定一开始所有空地上都没有军队。 

Input

第一行两个数n和Q分别表示树的点数和幽香操作的个数，其中点从1到n标号。 接下来n-1行，每行三个正整数a,b,c，表示a和b之间有一条边权为c的边。 接下来Q行，每行两个数u,e，表示幽香在点u上放了e单位个军队（如果e<0，就相当于是幽香在u上减少了|e|单位个军队，说白了就是du←du+e）。数据保证任何时刻每个点上的军队数量都是非负的。 

Output

 对于幽香的每个操作，输出操作完成以后，每天的最小花费，也即如果幽香选择最优的补给点进行补给时的花费。 

Sample Input

10 5
1 2 1
2 3 1
2 4 1
1 5 1
2 61
2 7 1
5 8 1
7 91
1 10 1
3 1
2 1
8 1
3 1
4 1

Sample Output

0
1
4
5
6

HINT

 

对于所有数据，1<=c<=1000, 0<=|e|<=1000, n<=10^5, Q<=10^5
 
问题就是算带修改带权重心。
考虑用动态树分治来做，建出重心树后就可以保证树高logn了。
那么我们先考虑如何计算一个点到所有点的带权距离（带修改）
对于一个节点Y，它的父亲x将贡献v2+v1*(w(x,y))的权值。
在重心树上不停地向根走，将所有权值累加即可。
那么怎么求重心呢？考虑先将重心设为root，每次更新。
如果当前的重心成了x，注意重心只可能在x最大的子树中。
具体看代码
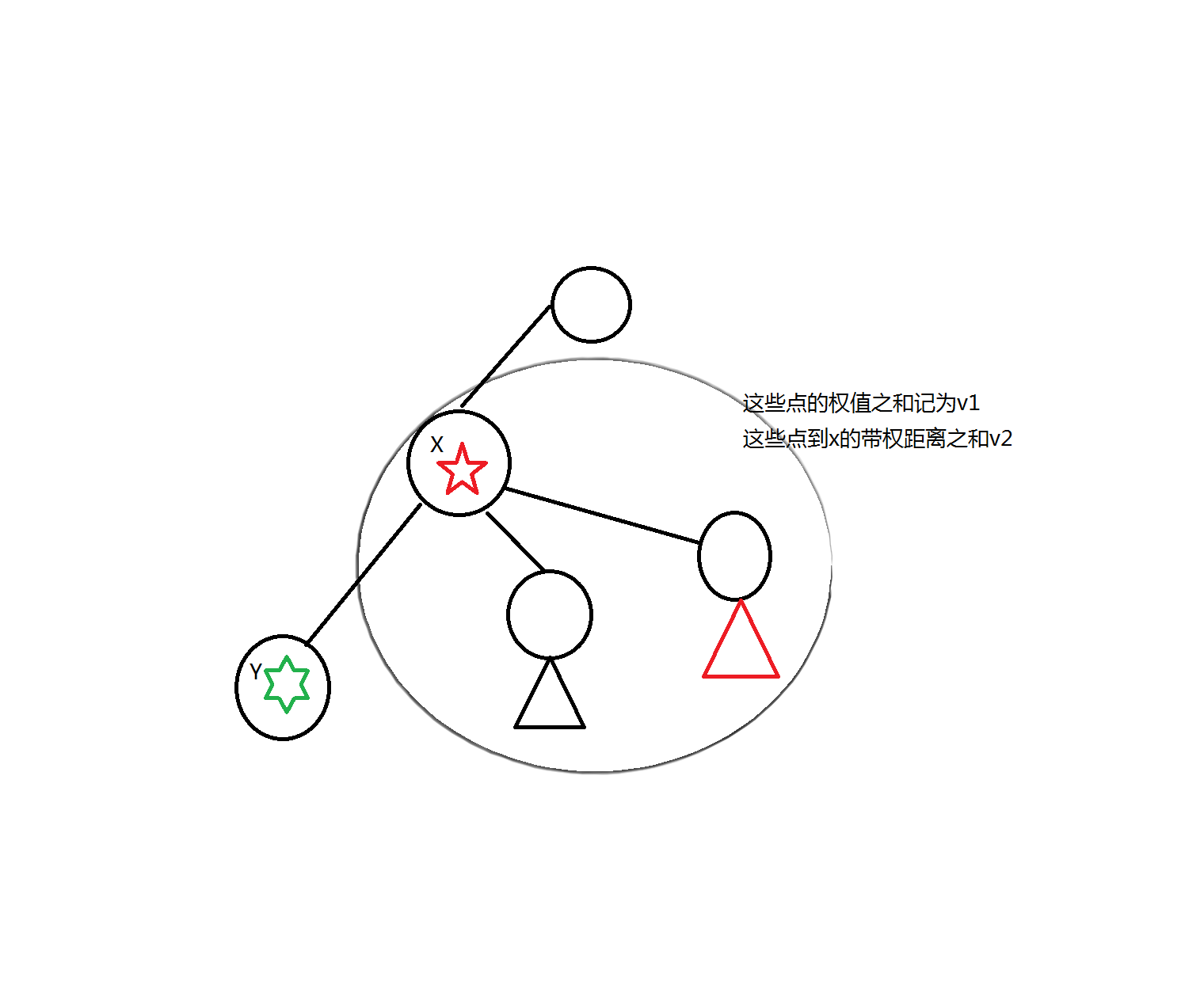
#include<cstdio>
#include<cctype>
#include<queue>
#include<cstring>
#include<algorithm>
#define rep(s,t) for(int i=s;i<=t;i++)
#define ren for(int i=first[x];i;i=next[i])
#define ren2 for(int i=first2[x];i;i=next2[i])
using namespace std;
inline int read() {
    int x=0,f=1;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*f;
}
typedef long long LL;
const int maxn=200010;
int n,m,first[maxn],next[maxn],es;
struct Edge {int to,dist;}edges[maxn];
void AddEdge(int w,int v,int u) {
    edges[++es]=(Edge){v,w};next[es]=first[u];first[u]=es;
    edges[++es]=(Edge){u,w};next[es]=first[v];first[v]=es;
}
int first2[maxn],next2[maxn],to[maxn],num[maxn],es2;
void AddEdge2(int u,int v,int w) {
    to[++es2]=v;num[es2]=w;next2[es2]=first2[u];first2[u]=es2;
}
int mn[maxn][21],Log[maxn],pos[maxn],dep[maxn],cnt;
void dfs(int x,int fa) {
    mn[++cnt][0]=dep[x];pos[x]=cnt;
    ren {
        Edge& e=edges[i];
        if(e.to!=fa) {
            dep[e.to]=dep[x]+e.dist;dfs(e.to,x);
            mn[++cnt][0]=dep[x];
        }
    }
}
int dist(int x,int y) {
    int ans=dep[x]+dep[y],k;
    x=pos[x];y=pos[y];if(x>y) swap(x,y);
    k=Log[y-x+1];return ans-min(mn[x][k],mn[y-(1<<k)+1][k])*2;
}//In order to get the LCA of x and y for nlogn times,we should use the "LCA-RMQ algorithm" to calculate.
int root,size,s[maxn],f[maxn],vis[maxn];
void getroot(int x,int fa) {
    s[x]=1;int maxs=0;
    ren {
        Edge& e=edges[i];
        if(!vis[e.to]&&e.to!=fa) getroot(e.to,x),s[x]+=s[e.to],maxs=max(maxs,s[e.to]);
    }
    f[x]=max(maxs,size-s[x]);
    if(f[root]>f[x]) root=x;
}
int fa[maxn];
void solve(int x,int F) {
    vis[x]=1;fa[x]=F;
    ren {
        Edge& e=edges[i];
        if(!vis[e.to]) {
            size=f[0]=s[e.to];getroot(e.to,root=0);
            AddEdge2(x,root,e.to);
            solve(root,x);
        }
    }
}
LL sum[maxn],dis1[maxn],dis2[maxn];
//sum1[x]=sigma(y's val) | y is included in x's subtree.
//dis1[x]=sigma(dist(x,y)) | y is included in x's subtree.
//dis2[x]=sigma(dist(fa[x],y)) | y is included in x's subtree.
void add(int x,int v) {
    sum[x]+=v;
    for(int i=x;fa[i];i=fa[i]) {
        int d=dist(fa[i],x);
        dis1[fa[i]]+=(LL)d*v;
        dis2[i]+=(LL)d*v;
        sum[fa[i]]+=v;
    }
}
LL cal(int x) {
    LL ret=dis1[x];
    for(int i=x;fa[i];i=fa[i]) {
        int d=dist(fa[i],x);
        ret+=dis1[fa[i]]-dis2[i];
        ret+=d*(sum[fa[i]]-sum[i]);
    }
    return ret;
}
LL query(int x) {
    LL ans=cal(x);
    ren2 {
        LL tmp=cal(num[i]);// Consider x's subnode y in previous tree, if the result is smaller than x then the center of gravity must be in y's conquer 's tree.
        if(tmp<ans) return query(to[i]);
    }
    return ans;
}
int main() {
    n=read();m=read();
    rep(1,n-1) AddEdge(read(),read(),read());
    dfs(1,0);Log[0]=-1;
    rep(1,cnt) Log[i]=Log[i>>1]+1;
    for(int j=1;(1<<j)<=cnt;j++)
       for(int i=1;i+(1<<j)-1<=cnt;i++)
          mn[i][j]=min(mn[i][j-1],mn[i+(1<<j-1)][j-1]);//pre-process
    size=f[0]=n;getroot(1,root=0);
    int t=root;solve(root,0);root=t;
    while(m--) {
        int x=read(),v=read();
        add(x,v);
        printf("%lld\n",query(root));
    }
    return 0;
}
View Code

 

posted @ 2015-07-09 11:41  wzj_is_a_juruo  阅读(562)  评论(0)  编辑  收藏  举报