博客作业06--图

1.学习总结

1.1图的思维导图

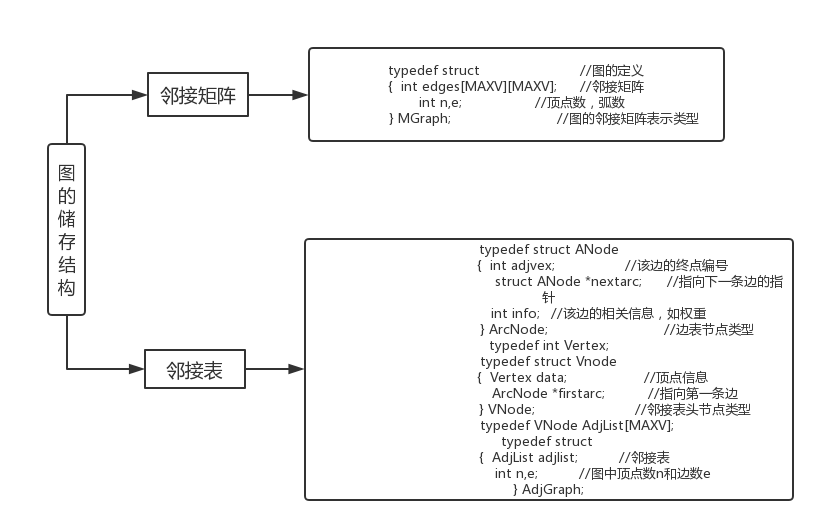
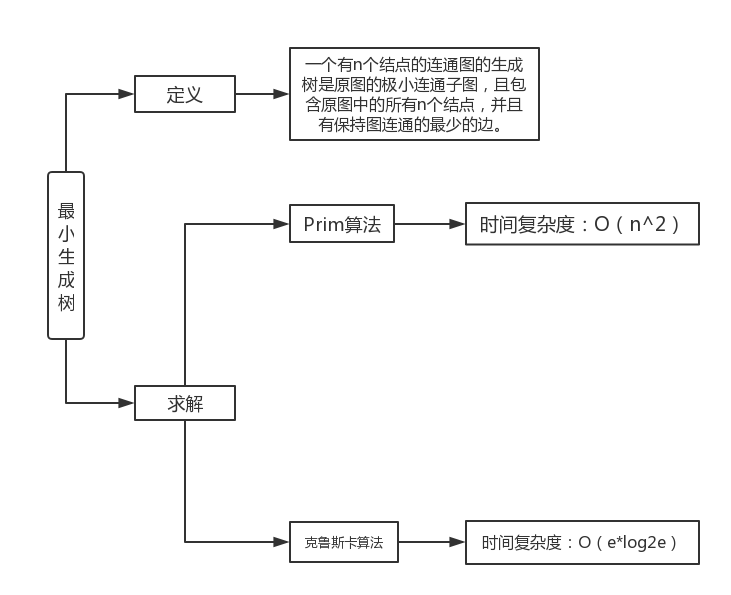
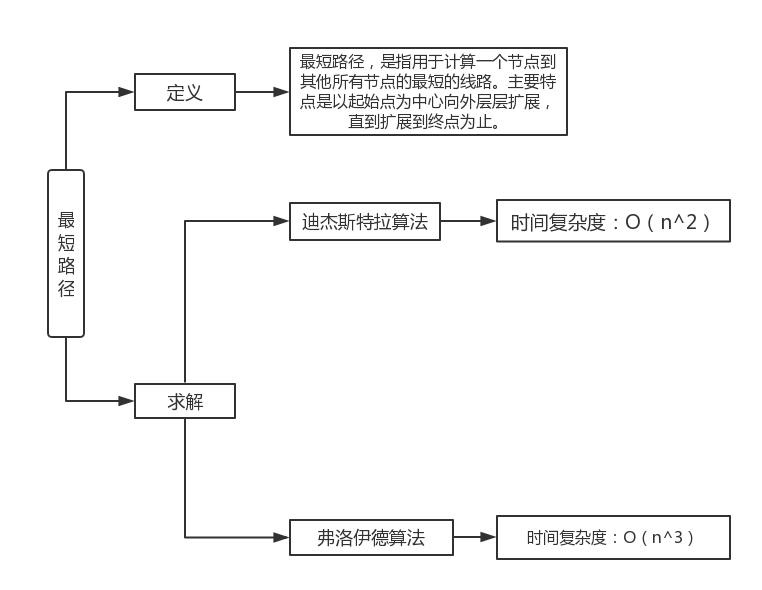
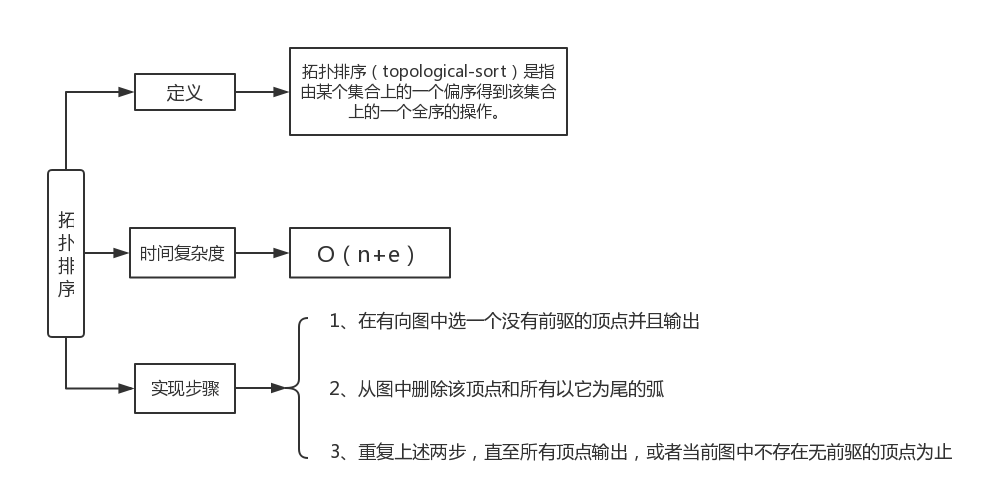
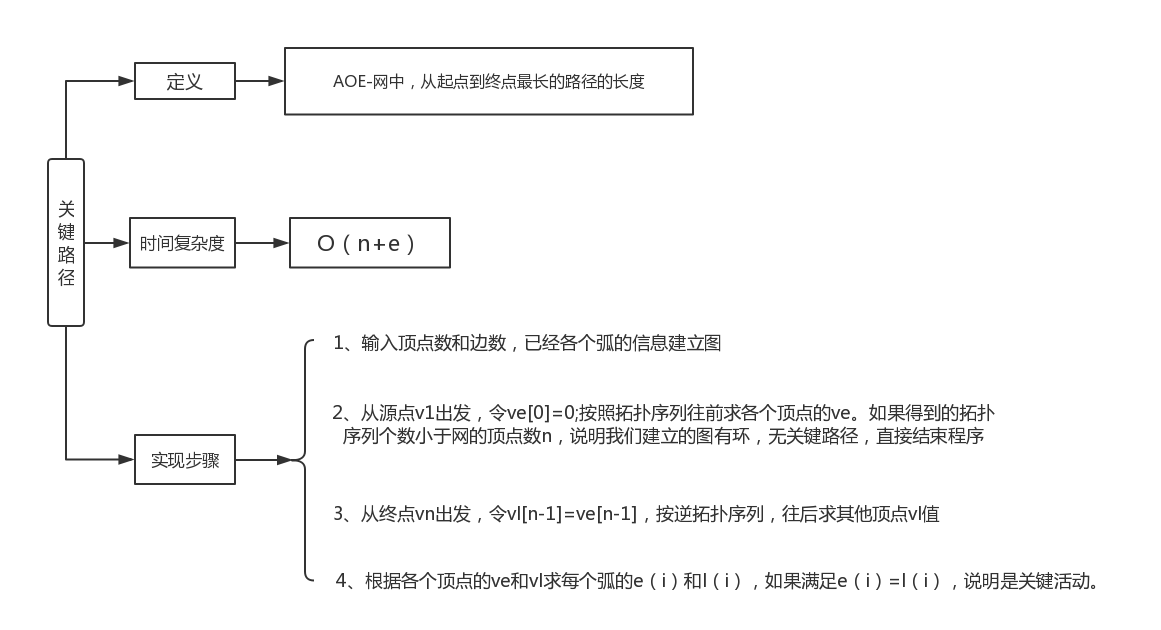
1.2 图结构学习体会

对于深度遍历和广度遍历算法，个人认为还是比较简单和易理解的，值得注意的是广度遍历需要用到队列；而对于最小生成树的Prim和Kruscal算法以及最短路径的Dijkstra算法，他们的原理我能够轻松理解，不过在代码上我并不是明白的很透彻，还需要多多研究；还有拓扑排序的算法，拓扑排序的原理和代码都很简单易懂，需要注意拓扑排序代码中需要用到栈

2.PTA实验作业

2.1 题目1：7-1 图着色问题

2.2 设计思路

建图
然后调用深度遍历函数将深度遍历结果储存于数组d中
输入颜色分配方案数目n
while（n--）
{
    for i=1 to  顶点数
       输入颜色方案并计算颜色数目
    判断颜色数目是否与k相等，不等令flag=0
    将颜色按深度遍历排序储存在数组e中 
   for i=0 to 顶点数
       for j=0 to 顶点数
          如果g->a[d[i]][d[j]]==1即存在边且e[i]==e[j]颜色相等 
              令flag=0且退出循环
   如果flag=0 输出no 否则 输出yes
}

2.3 代码截图

2.4 PTA提交列表说明

我一开始使用邻接表来做，但是大部分点都会段错误，所以我改用邻接矩阵来做

2.1 题目2：7-3 六度空间

2.2 设计思路

定义一个队列，count记录与该结点距离不超过6的结点数 ，level记录层数，last记录每一层访问的最后一个节点
先让起始点入队
while（队列不为空）
{
    第一个元素出队 并存入de
    for i=0   to  n-1
    如果G[de][i] && !visited[i]
       visited[i] = true代表已判断过
       将i进队
       count加一
       tail=i
    如果de=last
       层数加一
       last=tail
    如果层数等于6 退出循环
}
返回count

2.3 代码截图

2.4 PTA提交列表说明

建图的时候没建好，顶点编号从1开始，图是从0开始，输入值应该要减一，后面改的时候打快了，a--和b--都敲成b--了，没发现，最后从头看了一遍才发现

2.1 题目3：7-7 旅游规划

2.2 设计思路

主函数：Dijkstra函数
定义x
往dist和cost（分别代表距离和价格）存入初始值
初始化起点s的dist，cost，visit的值，其中dist和cost置为零，visit置为一
while（1）
   调用Findmindist函数寻找最小的V的邻边
   如果没找到 退出循环
   否则 visit[x]=1代表已经过
   for w=0  to  v-1
       如果!visit[w] && G[x][w].length < INF
          如果即路径长度更小的时候 
             修改路径长度和价格
          如果路径长度相同但价格更少
              修改价格

2.3 代码截图

2.4 PTA提交列表说明

一开始价格问题没处理好，输出的价格有误，判断的时候不一定是在相等路径长度下比较价格

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的总分：140

4. 阅读代码

代码中的粗部分与原拓扑序列的算法区别。

第11-15行 初始化全局变量etv数组。

第21行 就是讲要输出的拓扑序列压入全局栈。

第 27-28 行很关键，它是求etv数组的每一个元素的值。

ete表示活动<Vk,Vj>的最早开工时间，是针对弧来说的。

但是只有此弧的弧尾顶点Vk的事件发生了，它才可以开始，ete=etv[k]。

lte表示的是活动<Vk,Vj>最晚开工时间，但此活动再晚也不能等V1事件发生才开始。

而必须要在V1事件之前发生，所以lte=ltv[j]-len<Vk,Vj>。