BP神经网络
秋招刚结束,这俩月没事就学习下斯坦福大学公开课,想学习一下深度学习(这年头不会DL,都不敢说自己懂机器学习),目前学到了神经网络部分,学习起来有点吃力,把之前学的BP(back-progagation)神经网络复习一遍加深记忆。看了许多文章发现一PPT上面写的很清晰,就搬运过来,废话不多说,直入正题:
单个神经元
神经网络是由多个“神经元”组成,单个神经元如下图所示:
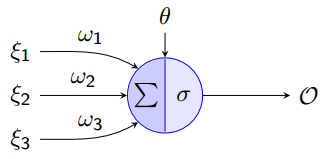
这其实就是一个单层感知机,输入是由ξ1 ,ξ2 ,ξ3和Θ组成的向量。其中Θ为偏置(bias),σ为激活函数(transfer function),本文采用的是sigmoid函数![]() ,功能与阶梯函数(step function)相似控制设神经元的输出,它的优点是连续可导。
,功能与阶梯函数(step function)相似控制设神经元的输出,它的优点是连续可导。
![]() 是神经元的输出,结果为
是神经元的输出,结果为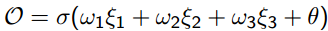
可以看得出这个“神经元”的输入-输出映射其实就是一个逻辑回归,常用的激活函数还有双曲正切函数 。
激活函数
sigmoid:函数

取值范围为[0,1],它的图像如下:
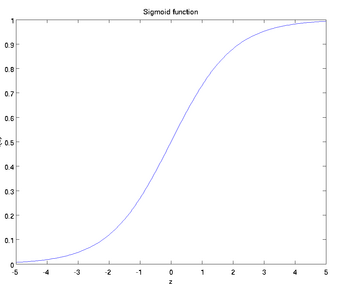
求导结果为:

tanh函数:
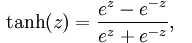
取值范围为[-1,1],图像如下:
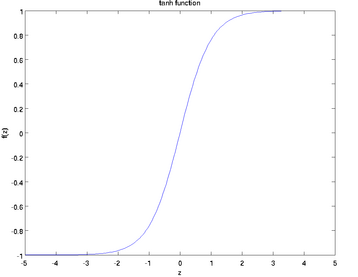
求导数结果为![]() 。本文采用的是sigmoid函数作为激活函数。
。本文采用的是sigmoid函数作为激活函数。
神经网络模型
神经网络将许多“神经元”联结在一起,一个神经元的输出可以是另一个“神经元”的输入,神经元之间的传递需要乘法上两个神经元对应的权重,下图就是一个简单的神经网络:
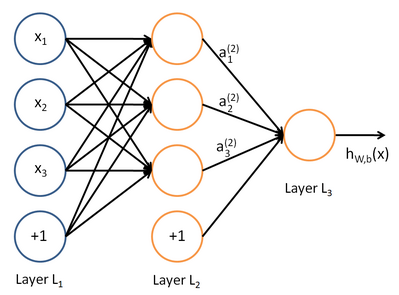
这是一个三层的神经网络,使用圆圈来表示神经元的输入,“+1”被称为偏置节点,从左到右依次为输入层、隐藏层和输出层,从图中可以看出,有3个输入节点、3个隐藏节点和一个输出单元(偏置不接受输入)。
本例神经网络的参数有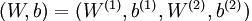 ,其中
,其中 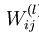 是第l层第 j 单元与 l+1层第
是第l层第 j 单元与 l+1层第  单元之间的联接参数,即:节点连线的权重,本图中
单元之间的联接参数,即:节点连线的权重,本图中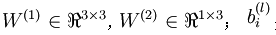 是第l+1 层第i单元的偏置项。
是第l+1 层第i单元的偏置项。
向前传播
机器学习(有监督)的任务无非是损失函数最小化,BP神经网络的原理是前向传播得到目标值(分类),再通过后向传播对data loss进行优化求出参数。可见最优化部分
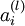 表示
表示 层第
层第  单元激活值(输出值)。当
单元激活值(输出值)。当 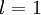 时,
时, 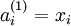 ,也就是第
,也就是第  个输入值。对于给定参数集
个输入值。对于给定参数集 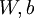 ,
,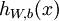 来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下:
来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下:
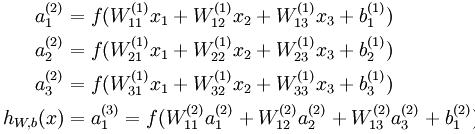
可以看出,神经网络的核心思想是这一层的输出乘上相应的权重加上偏置,带入激活函数后的输出又是下一层的输入。用 ![]() 表示第
表示第 层第
层第 单元输入加权和
单元输入加权和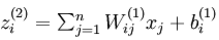 ,则
,则 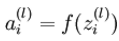 。使用向量化表示方法表示,上面的公式可以简写为:
。使用向量化表示方法表示,上面的公式可以简写为:

这些计算步骤就是前向传播,将计算过程进行推广,给定第  层的激活值
层的激活值 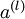 ,第
,第  层的激活值
层的激活值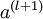 的计算过程为:
的计算过程为:
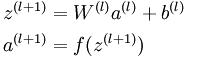
反向传播
在前向传播中,我们得到了神经网络的预测值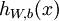 ,这时候可以通过反向传播的方法计算出参数
,这时候可以通过反向传播的方法计算出参数
符号定义
 :第l层第j个节点的输入。
:第l层第j个节点的输入。
 :从第l-1层第i个节点到第l层第j个节点的权值。
:从第l-1层第i个节点到第l层第j个节点的权值。
 :Sigmoid激活函数。
:Sigmoid激活函数。
 ::第l层第j个节点的偏置。
::第l层第j个节点的偏置。
 ::第l层第j个节点的输出。
::第l层第j个节点的输出。
 ::输出层第j个节点的目标值(label)。
::输出层第j个节点的目标值(label)。
使用梯度下降的方法求解参数,在求解的过程中需要对输出层和隐藏层分开计算
输出层权重计算
给定样本标签 和模型输出结果
和模型输出结果 ,输出层的损失函数为:
,输出层的损失函数为:

这其实就是均方差项,训练的目标是最小化该误差,使用梯度下降方法进行优化,对上式子对权重W进行求导:

,整理 ,
,
其中 =
= 带入
带入 ,对sigmoid求导得:
,对sigmoid求导得:

输出层第k个节点的输入 等于上一层第j个节点的输出
等于上一层第j个节点的输出 乘上
乘上 ,即
,即 =
=
 ,而上一层的输出
,而上一层的输出 与输出层的权重变量
与输出层的权重变量 无关,可以看做一个常数,所以直接求导可以得到:
无关,可以看做一个常数,所以直接求导可以得到:
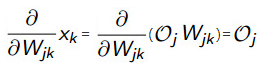
所以将 =
= 带入式子中就得到:
带入式子中就得到:
![]()
为了方便表示将上式子记作:

其中:

隐藏层权重计算
采用同样方法对隐藏层的权重进行计算,与前面不同的是关于隐藏层和前一层权重的调整

整理

替换sigmoid函数

对sigmoid求导

把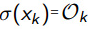 带入进去,使用求导的链式法则:
带入进去,使用求导的链式法则:

输出层的输入等于上一层的输入乘以相应的权重,即: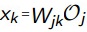 于是得到
于是得到

对![]() 进行求导(
进行求导( =
= ,同样适用于j),
,同样适用于j),

同输出层计算的方法一样,再次利用![]() ,j换成i,k换成j同样成立,带入进去:
,j换成i,k换成j同样成立,带入进去:

整理,得到:

其中:
我们还可以仿照 的定义来定义一个
的定义来定义一个 ,得到:
,得到:

其中:
偏置调整
从上面的计算步骤中可以看出:例如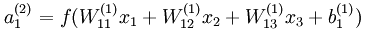 ,偏置节点是不存在对应的权值参数,也就是不存在关于权值变量的偏导数。
,偏置节点是不存在对应的权值参数,也就是不存在关于权值变量的偏导数。
对偏置直接求导:

又有

得到:
 ,其中:
,其中:
BP算法步骤
1. 随机初始化W和b,需要注意的是,随机初始化并是不是全部置为0,如果所有参数都是用相同的值初始化,那么所有隐藏单元最终会得到与输入值相关、相同的函数(也就是说,对于所有  ,
,![]() 都会取相同的值,那么对于任何输入
都会取相同的值,那么对于任何输入  都会有:
都会有: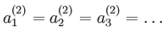 ),随机初始化的目的是使对称失效。
),随机初始化的目的是使对称失效。
2.对每个输出节点按照这个公式计算delta:
![]()
3.对每个隐藏节点按照这个公式计算delta:

4.更新W和b的公式为:

并更新参数 ,这里的η是学习率。
,这里的η是学习率。
Reference
2.反向传导算法



 浙公网安备 33010602011771号
浙公网安备 33010602011771号