cs231n笔记：线性分类器

cs231n线性分类器学习笔记，非完全翻译，根据自己的学习情况总结出的内容：

线性分类

　　本节介绍线性分类器，该方法可以自然延伸到神经网络和卷积神经网络中，这类方法主要有两部分组成，一个是评分函数(score function)：是原始数据和类别分值的映射，另一个是损失函数：它是用来衡量预测标签和真是标签的一致性程度。我们将这类问题转化为优化问题，通过修改参数来最小化损失函数。

　　首先定义一个评分函数，这个函数将输入样本映射为各个分类类别的得分，得分的高低代表该样本属于该类别可能性的高低。现在假设有一个训练集，每个样本都有一个对应的分类标签y_i，这里i=1,2....N，并且y_i ∈ 1…K，这里，N代表样本个数，样本的维度为D，共有K个类别。定义评分函数：，该函数是原始样本到分类分值的一个映射。

　　线性分类器：先介绍最简单的线性映射：，在公式中，每一个输入样本都被拉成一个长度为D的列向量，其中W和b都是参数，参数W被称为权重(weights)大小为K x D 和，参数b为偏置向量(bias vector)大小K x 1，它影响输出结果，但是并不和原始样本产生关联。卷积神经网络样本到分类分值的方法和上面一样，但是映射函数f（x）将更加的复杂，参数也更多。

解释线性分类器

　　线性分类器各维度的值与权重相乘，从而得到分类分值。如下图：首先将这张猫咪的图片拉伸成一个列向量，与矩阵W相乘，然后得到各个分类的值，可以看出得

到的评分中，猫的评分很低，则这个矩阵W并不好。我们还可以将样本看做高维空间中的一个样本点，整个数据集就是一个空间点的集合，每个点都有一个标签，则每个分类类别的分值就是这个空间中一条线性函数的函数值。

偏置和权重的合并技巧：分类的评分函数为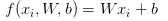，分开处理参数W、b有点麻烦，一般常用方法是将W和b合并到同一个矩阵中，同时x_i这个向量要增加一个维度，数值为1。具体见下图：

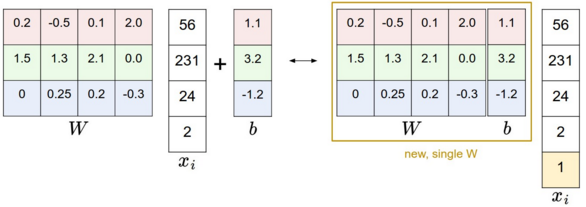
左边是先做矩阵乘法然后做加法，右边是权重矩阵增加一个偏置列，输入向量维度增加1，然后做矩阵乘法。这样的好处是只用学习到一个权重矩阵。

损失函数 loss function

 　　评分函数的参数是矩阵W，数据（x_i，y_i）是给定的不能修改，我们可以通过修改参数矩阵W来调整，来使评分函数与真实的类别一致，即：真实类别的评分应该是最高的。我们使用损失函数（loss function）来衡量对结果的不满意程度。当评分函数与真实结果相差越大时，损失函数的值也就越大。

 多类别支持向量机损失(Muliticlass SVM Loss)

　　损失函数的类别有很多种，首先介绍多类别SVM损失函数，SVM的损失函数要SVM在正确类别上的得分要比不正确类别上的得分高出一个Δ，针对第i个样本的损失函数为：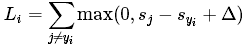

称为合页损失函数（hinge loss），其中:为第j个类别的得分，y_i是正确类别的标签。举例：假设有3个类别，s=[13,-7,11]。其中第一个类别是正确类别，假设Δ的值为10，损失函数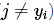（为两部分的和：

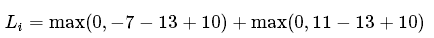
第一部分的值为0，第二部分的值为8。SVM的损失函数想要正确分类类别yi的分数要比不正确分类的分数高，而且至少要高一个Δ（可以这样写s_j+Δ <=s_yi），如果不满足这一点，就需要计算损失值。更加形象化的如图所示

“SVM的损失函数想要正确分类类别yi的分数要比不正确分类的分数高，而且至少要高一个Δ”，如果其他类别分数进入红色区域，甚至更高，那么就需要计算损失，否则损失为0。我们的目标是找到一些权重，它们既能够这样的要求，又能让损失值尽可能的小。

 正则化（Regularization）：上面损失函数有一个问题，假设一组数据和权重W能够对每个样本正确分类，即：对所有i都有Li=0;问题在于这个W并不唯一，例如W能使损失值都为0，当λ>1时，任何λW都能使损失值为0。所以我们希望向特定的权重W添加某些偏好，来消除不确定性，可以通过添加正则化惩罚（regularization penalty）来完成，常用的正则化项是L2范式，它通过对所有参数进行逐元素平方惩罚来抑制较大的权重：

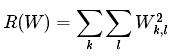
上面式子仅包含权重W，不包含样本，将W所有元素平方求和。给出完整的多分类SVM的损失函数，包含两部分：数据损失，即所有样本的平均损失和正则化损失：

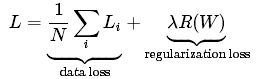展开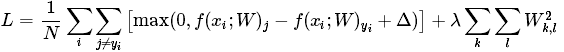

其中N代表训练样本的个数，λ表示正则化项的权重，它的确定需要动过cross-validation。

　　L2的一个最大的性质是对大数值权重的惩罚，提升泛化能力，这就消除了某一个维度对整体分值影响过大的影响。eg：输入向量x=[1,1,1,1],有两个权重向量w1=[1,0,0,0],w2=[0.25,0.25,0.25,0.25],那么w1^Tx = w2^Tx = 1，两个权重向量得到相同的分值1，根据L2惩罚来看W2更好，因为它的正则化损失值更小。W2惩罚倾向于更小更分散的的权重向量，这样就能鼓励分类器将所有维度上的特征都使用起来。通常只对权重w 进行正则化，而不正则化偏置b。

代码：无正则化部分的损失函数，非向量化和半向量化损失的代码实现

def hinge_unvectorized(x,y,W):
    """
    实现hinge loss function，非向量化
    -x 样本，是一个列向量
    -y 样本的类别的标签
    -W 权重矩阵
    返回第i条样本的损失值
    """
    delta = 1.0
    scores = W.dot(x)#每一个类别的得分，N x 1
    correct_class_score = scores[y]#正确类别的得分
    N = W.shape[0] #类别的个数
    loss_i = 0.0 #第i个样本的loss值
    for j in range(N):
        if j == y:
            continue#跳过正确的类别，循环其他incorrect classes
        loss_i += max(0,scores[j] - correct_class_score + delta)
    return loss_i

 

半向量化实现方式

def hinge_halfVectorized(x,y,W):
    """
    半向量化的实现方式
    """
    delta = 1.0
    scores = W.dot(x)
    #使用向量方法计算出各个类别的margins
    margins = np.maximum(0,scores - scores[y] + delta)#maximum
    margins[y] = 0 #减去yi的score
    loss_i = np.sum(margins)#求和
    return loss_i

 

超参数delat和λ对损失函数中的数据损失和正则化损失之间权衡，权重W的大小对于分类分值有着直接的影响，对w进行缩小，那么分类之间的差值也会变小，反之亦然。权重的大小就能控制差异的变大或缩小，因此delta 为1或100是没有意义的。因此真正的权衡是我们允许权重变大到何种程度（λ来进行控制）。

 softmax分类器

　　softmax可以理解为逻辑回归泛化到多分类问题中，SVM分类器输出f（x_i,w）作为每个分类的评分（未标准化的，可能难以理解）。与SVM不同的是softmax输出的是归一化后的概率，更加的直观，可以从概率上给出解释。在softmax分类器中映射函数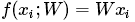保持不变，但将这些评分值看做每一类别未归一化的对数概率，损失函数为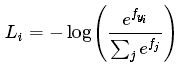，fj代表评分向量f中第j个元素的值。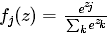为softmax函数，它的作用是对评分值进行压缩到[0,1]范围。

注意事项：数值稳定。编程实现softmax的时候，计算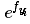时候数值可能非常的大，归一化的时候除以大数值会存在数值不稳定。做法是分子分母同时乘以常熟C，并变换到求和之中，得到下面公式

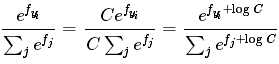
C的值可以自由选择，通常设置logC=-max(f_i)。这样将向量f中的数值进行平移，能提高计算的数值稳定性，例子如下：

f = np.array([123,456,789])#3个类别对应的分值，都比较大   
p = np.exp(f) / np.sum(np.exp(f))#溢出：结果array([  0.,   0.,  nan])
#将f中的值平移，令最大值为0
f -= np.max(f) #向量f减去max(f) f:array([-666, -333,    0])
p = np.exp(f) / np.sum(np.exp(f))#OK，结果正确

 

 关于命名规则：SVM分类器使用的是合页损失函数(hinge loss),有时又被称为最大边界损失(max-margin loss)。softmax分类器使用的是交叉熵损失（cross-entropy loss），softmax分类器的命名是从softmax函数那里得来，softmax函数将原始分类评分归一化到[0,1]，这样处理后才能应用到交叉熵。从技术熵说“softmax损失”是没有意义的。

SVM和softmax的对比

下图有助于理解SVM和softmax处理步骤的不同

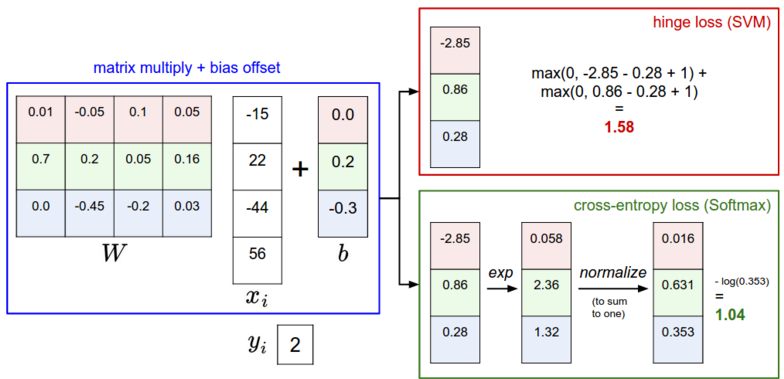
这个图举例说明了SVM和softmax在处理一个样本点的方式不同。两个分类器都是通过矩阵相乘的方式计算得到相同的分值向量f，不同之处在于对分值的解释：SVM将它看做是分类的评分，它的损失函数鼓励正确分类的分值比其他分类至少高出一个边界值(delta)。softmax分类器将这些分值看做是每个分类没有归一化的对数概率值，希望正确分类的归一化对数概率值最高，其他的低。

　　softmax分类器计算出的结果为eg:[0.9,0.09,0.01],这样就能得出所有分类标签的“可能性”，代表不同类别的自信程度。为什么要在“可能性”上面打上引号，这是因为可能性的集中(eg:[1,0,0])或离散程度([0.33,0.33,0.33])是由正则化参数λ决定，λ是我们能够直接控制的输入参数。举个栗子：

假设三个分类的原始分数是[1,-2,0],softmax计算结果如下：

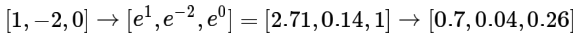
如果正则化参数λ变大，那么权重W就会被惩罚的更多，各个维度的权重数值会变小，softmax计算结果如下：

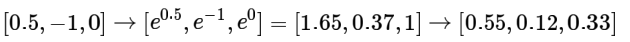
从例子可以看出，概率的分布变得更加分散了，如果随着λ的变大，权重W值会越来越小，最后输出的概率分布就接近均匀分布。这也就是说，softmax分类器得到的概率值的相对大小是对某种类别的自信程度。

举例对比SVM和softmax：与softmax相比，SVM更加的“local objective”，假设评分值为[10,-2,3]类别1为正确类别，SVM得到的损失函数为0，如果分数是[10, 9, 9] 甚至是 [10, -100, -100]，对于SVM来说只要满足边界值（margin or delta）大于等于1，损失值都为0.对于softmax，[10,9,9]计算出的损失值远远大于[10, -100, -100]，它希望正确分类值尽可能的大，错误分类值尽可能小，损失值尽可能的小。SVM只要求边界值被满足就可以了，不会去限制具体的分数。打比方来说：汽车分类器应该把精力花在如何分辨小轿车和大卡车上，而不应被青蛙样本所影响。因为青蛙的评分已经够低的了。