最长上升子序列O(nlogn)算法详解

最长上升子序列

时间限制: 10 Sec   内存限制:128 MB

题目描述

给定一个序列，初始为空。现在我们将1到N的数字插入到序列中，每次将一个数字插入到一个特定的位置。我们想知道此时最长上升子序列长度是多少？

输入

第一行一个整数N，表示我们要将1到N插入序列中，接下是N个数字，第k个数字Xk，表示我们将k插入到位置Xk（0<=Xk<=k-1,1<=k<=N）

输出

1行，表示最长上升子序列的长度是多少。

样例输入

3

0 0 2

样例输出

2

提示

100%的数据 n<=100000

O(nlogn)算法代码：

#include <iostream>
using namespace std; 
int i,j,n,s,t,a[100001];
int main()
{ 
    cin>>n;
    a[0]=-1000000;
    for(i=0;i<n;i++)
    {
        cin>>t;/* 比栈顶元素大数就入栈 */
        if(t>a[s]) a[++s]=t;
        else
        {
            int l=1,h=s,m;
/* 二分检索栈中比t大的第一个数 */
            while(l<=h)
            {
                m=(l+h)/2;
                if(t>a[m]) l=m+1;
                else h=m-1;
            }/* 用t替换 */
            a[l]=t;
        }
    }/* 最长序列数就是栈的大小 */
    cout<<s<<endl;
}

代码分析：

第一个念头就是用动态规划，很显然，这道题的转移方程非常非常简单，一目了然，先准备一个数组b

b[i]=1;
，从a[1]开始搜到i的最长上升子序列。

这句赋值语句固然很好理解，每一个元素，也可以视为一个符合题意的子序列。

b[2]呢？

如图，它显然比a[1]高，在执行如下语句时

for(j=1;j<i;j++)   if(a[i]>a[j])

j小于i，也就是2，目前符合条件的只有a[1]，a[1]又通过了判断语句，它确实小于a[i]，执行下一条语句：

b[i]=max(b[i],b[j]+1);

很显然:b[2]显然原来是1，当它和b[1]+1比时，1当然比2小，所以，b[2]自然就是2了。

再来看看时间复杂度：

很明显，时间复杂度为O(n^2)。

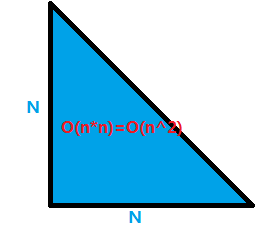
那，这个方法够快吗？还可以，但仍然有些不尽人意。

代码如下O(n^2)：

#include<iostream>  
using namespace std;
int i,j,n,a[100],b[100],max;    
int main()  
{
    cin>>n;
    for(i=0;i<n;i++) cin>>a[i];  
    b[0]=1; //初始化，以a[0]结尾的最长递增子序列长度为1  
    for(i=1;i<n;i++)  
    {  
        b[i]=1;//b[i]最小值为1
        for(j=0;j<i;j++)  
            if(a[i]>a[j]) b[i]=max(b[i],b[j]+1);
    }  
    for(max=i=0;i<n;i++) if(b[i]>max) max=b[i];  
    cout<<max<<endl;
}

那么，还有没有更快的方法呢？

当然有，有没有想到过，为什么要记录数据呢？

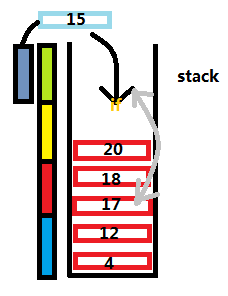
我们可以模拟一个stack

在有大量数据的情况下，这算法效率极高

但是，怎么来优化程序呢？

我们可以这样来模拟：

每输入一个数，如果这个数大于栈顶的那个数，于是把它推入栈中。

 

但是，如果这个数大于栈顶呢，这不证明它不可以更新栈中的

某个元素，这时，就可以运用二分查找了。

     有人可能会问：这个序列是无序的啊。没错，但查找的是stack里面的元素，而这个栈里的所有元素，都是严格递增的，所以，用二分查找可以把问题缩减为O(nlogn)。

     有些不符合逻辑，不是吗？15的下标比17、18、20都大，为什么能插入呢？但是如果仔细想一想，这好像并不影响正常答案，但如果要输出最长上升子序列，那就要改一改这个算法了。

整个二分查找代码如下：

else

{

    int l=1,h=s,m;

    while(l<=h)

    {

         m=(l+h)/2;

         if(t>a[m]) l=m+1;

         else h=m-1;

    }

    a[l]=t;

}

由此，这个查找算法才得以下降到logn，于是，整体也就是O(nlogn)。

具体操作如下:

每次取栈顶元素和读到的元素做比较,如果大于，则将它入栈；如果小于，则二分查找栈中的比它大的第1个数，并替换它。最长序列长度即为最后模拟的大小。

这也是很好理解的，对于i和j，如果i <j且a[i] < a[j],用a[i]替换a[j]，长度虽然没有改变但a的'潜力'增大了。

代码（同上）：

#include <iostream>
using namespace std; 
int i,j,n,s,t,a[100001];
int main()
{ 
    cin>>n;
    a[0]=-1000000;
    for(i=0;i<n;i++)
    {
        cin>>t;
        if(t>a[s]) a[++s]=t;
        else
        {
            int l=1,h=s,m;
            while(l<=h)
            {
                m=(l+h)/2;
                if(t>a[m]) l=m+1;
                else h=m-1;
            }
            a[l]=t;
        }
    }
    cout<<s<<endl;
}