查找

1.学习总结(2分)

1.1查找的思维导图

 

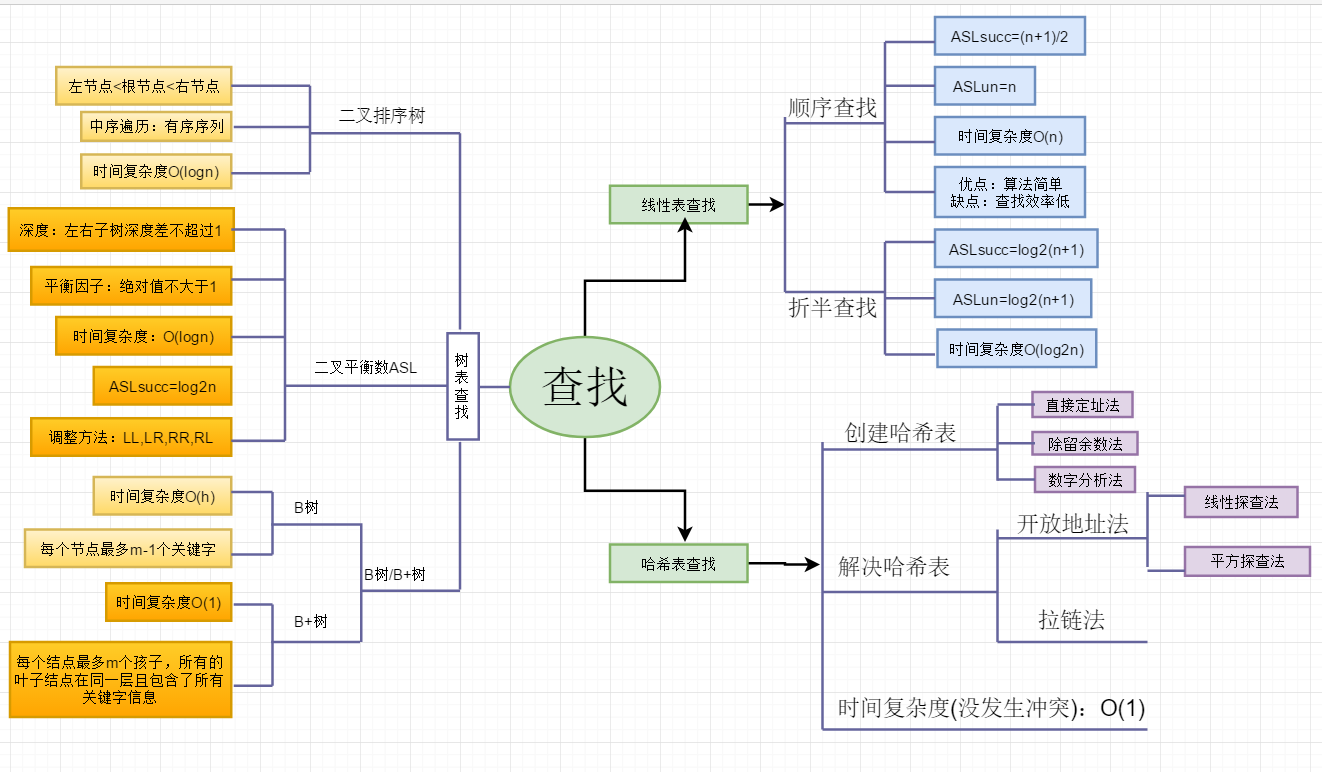
1.2 查找学习体会

查找的内容很多，线性表的查找，树表的查找，哈希表的查找等，又各有细分，每个查找方法的平均查找长度都不同，并有成功和不成功之分，效率也不尽相同，各有优缺点。

线性表查找中有3种查找法，其中以折半查找效率最高，但只适用于静态查找表，树表的查找则侧重于动态查找表，如二叉排序树，平衡二叉树等。BST和AVL树都是用作内部

查找的数据结构，即查找的数据集不大，可以放在内存中，而B-树和B树是用作外部查找的数据结构，其中的数据存放在外存中。

2.PTA实验作业（4分）

---

1 题目1：6-2 是否二叉搜索树

2 设计思路

bool IsBST ( BinTree T )

{

　　BinTree p;

　　如果T是二叉搜索树，则函数返回true，否则返回false；

　　非空左子树的所有键值小于其根结点的键值；

　　非空右子树的所有键值大于其根结点的键值；

}

3 代码截图

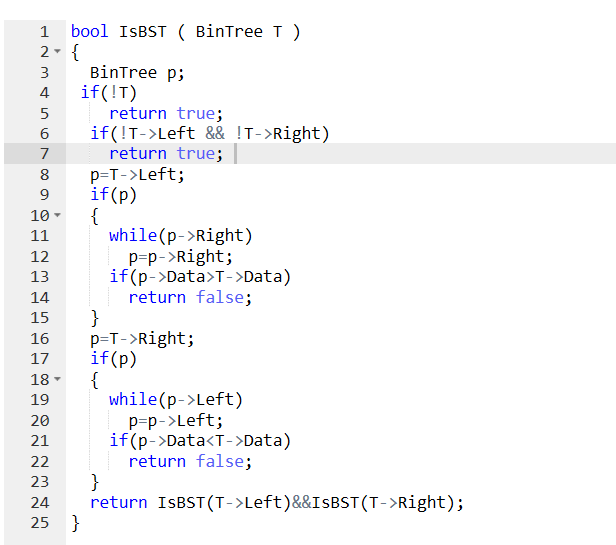
4 PTA提交列表说明

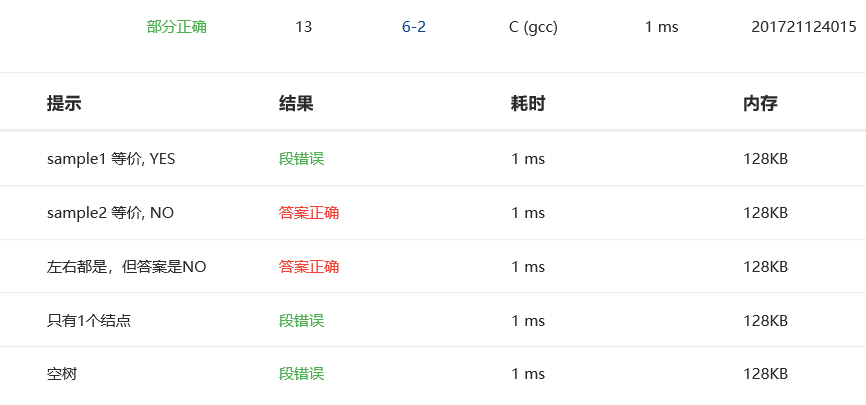
不是很明白段错误的意思，去查了一下“段错误就是指访问的内存超出了系统所给这个程序的内存空间”，只有一个结点和空树时通不过，段错误，

在考虑非空左子树的所有键值小于其根结点的键值，非空右子树的所有键值大于其根结点的键值时考虑不够周全，写错了，再改了调试一下。

 

1 题目2：6-3 二叉搜索树中的最近公共祖先

2 设计思路

int LCA( Tree T, int u, int v )
{

　　分多次讨论p!=NULL时；

　　树T中两个结点u和v的最近公共祖先结点的键值；

　　找到即find=0；

　　若u或v不在树中，则应返回error；

}

3 代码截图

 

 

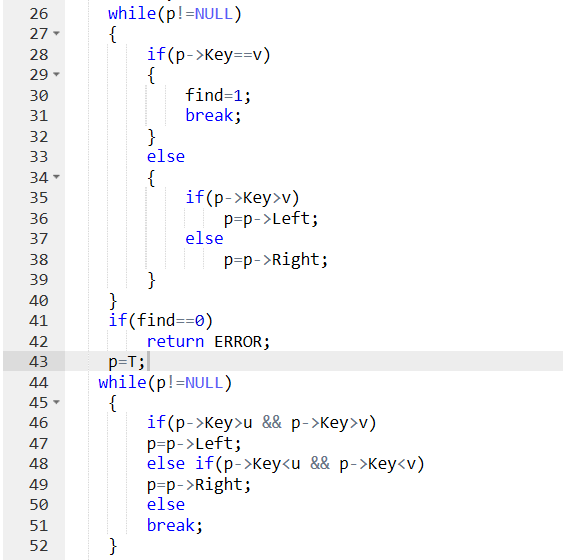
4 PTA提交列表说明

 

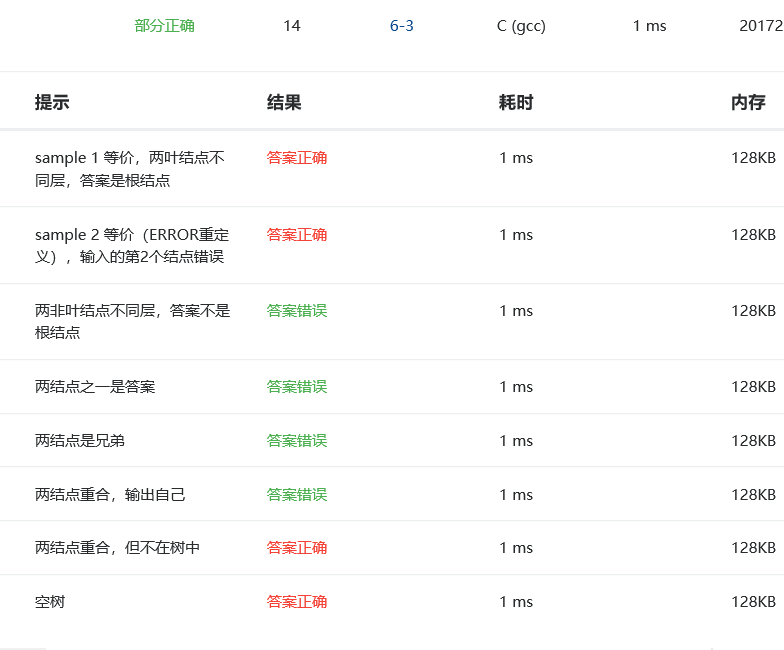
 在两结点重合的情况下，不在树中通过了，但是输出自己没有通过，还有其他两结点的情况也没能通过，再仔细看一下，是自己考虑的不够周全，

确实在两节点时，一开始的想法是不够完整的，在一棵树T中两个结点u和v的最近公共祖先(LCA)，是树中以u和v为其后代的深度最大的那个结点。

函数LCA须返回树T中两个结点u和v的最近公共祖先结点的键值。若u或v不在树中，则应返回ERROR。

 

1 题目2：

1 题目2：7-1 QQ帐户的申请与登陆

2 设计思路

int main()

{

　　申请空间

　　一个大for循环

　　{

　　　　命令符为“L”（代表Login）时表示是老帐户登陆，后面是登陆信息;

　　　　命令符为“N”（代表New）时表示要新申请一个QQ号，后面是新帐户的号码和密码;

　　}

}

3 代码截图

 

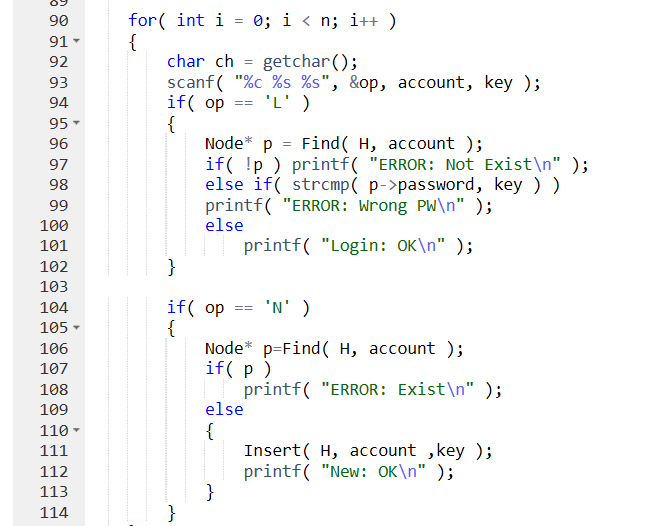
4 PTA提交列表说明

 

运行时错误，觉得应该是运行超时了， 一开始老师提示说用C++的map时不是很懂，听不明白，想到的思路是文件，百度一下好好了解，觉得还是很实用的。

超时是我数组溢界了，修改一下就好。

 

---

3.截图本周题目集的PTA最后排名（3分）

3.1 PTA排名（截图带自己名字的排名）

 

4. 阅读代码（必做，1分）

红黑树的节点声明，其中Parent指针是指向某一节点的父节点的指针：

typedef struct TreeNode *PtrRBTNode;
typedef struct TreeNode RBTNode;
struct TreeNode{
    ElementType Key;
    ColorType Color;
    PtrRBTNode Left;
    PtrRBTNode Right;
    PtrRBTNode Parent;
};

红黑树的总体声明，该声明中包含了指向红黑树根节点的指针和指向用作sentinel的dummy node的指针：

typedef struct Tree *PtrRBT;
struct Tree{
    PtrRBTNode Root;
    PtrRBTNode NullNode;
};

一些其他的相关函数：

PtrRBT RBInit(PtrRBT T){
    T = (PtrRBT)malloc(sizeof(struct Tree));
    T->Root = NULL;
    T->NullNode = (PtrRBTNode)malloc(sizeof(RBTNode));
    T->NullNode->Key = -1;
    T->NullNode->Color = Black;
    T->NullNode->Left = T->NullNode->Right = T->NullNode->Parent = NULL;
    
    return T;
}

PtrRBTNode RBCreateNode(PtrRBT T, ElementType Val){
    PtrRBTNode NewNode = (PtrRBTNode)malloc(sizeof(RBTNode));
    
    NewNode->Key = Val;
    NewNode->Color = Red;
    NewNode->Left = NewNode->Right = T->NullNode;
    
    return NewNode;
}

PtrRBTNode RBSearch(PtrRBT T, ElementType Val){
    PtrRBTNode TempNode = T->Root;
    
    if(NULL == TempNode){
        return NULL;
    }
    while(T->NullNode != TempNode){
        if(TempNode->Key > Val){
            TempNode = TempNode->Left;
        }
        else if(TempNode->Key < Val){
            TempNode = TempNode->Right;
        }
        else{
            return TempNode;
        }
    }
    
    return NULL;
}

PtrRBTNode RBFindSuccessor(PtrRBT T, PtrRBTNode Root){
    while(T->NullNode != Root->Left){
        Root = Root->Left;
    }
    
    return Root;
}

Rotate

---

红黑树的旋转操作和AVL树的旋转操作差不多，但是还是有几个需要特别注意的地方。

首先，应当注意红黑树的每个节点都有Parent指针，在旋转操作时不能遗漏对于Parent指针的操作。

第二，对于某一节点中Parent指针的操作需要访问该节点，这时就应当注意该节点是否为NULL节点。例如下图中的C节点就可能为NULL节点，如果不是NULL节点，在旋转时要将C的Parent指针指向B。当然在处理NULL节点时，我们可以利用一个dummy node来作为一个sentinel，所有的叶节点的Left和Right指针都指向这个sentinel，而根节点的Parent指针也指向sentinel，sentinel的Color为Black，其余成员值为任意。

第三，在旋转时应该注意根节点。当旋转的Pivot节点就是根节点时，应当注意更改struct Tree结构中的Root指针，将其指向新的根节点。当旋转的Pivot节点不是根节点时，应当注意更改Pivot的父节点的Left或Right指针，这里就需要加以分类讨论（到底新的根节点，如上图中的D节点，是其父节点的左子树还是右子树），可以利用Pivot->Parent来访问Pivot的父节点。

Source Code

PtrRBT RBLeftRotate(PtrRBT T, PtrRBTNode Pivot){
    PtrRBTNode TempNode = Pivot->Right;
    
    Pivot->Right = TempNode->Left;
    if(T->NullNode != TempNode->Left){
        TempNode->Left->Parent = Pivot;
    }
    TempNode->Left = Pivot;
    TempNode->Parent = Pivot->Parent;
    if(T->Root == Pivot){
        T->Root = TempNode;
    }
    else{
        if(Pivot == Pivot->Parent->Left){
            Pivot->Parent->Left = TempNode;
        }
        else{
            Pivot->Parent->Right = TempNode;
        }
    }
    Pivot->Parent = TempNode;
    
    return T;
}

PtrRBT RBRightRotate(PtrRBT T, PtrRBTNode Pivot){
    PtrRBTNode TempNode = Pivot->Left;
    
    Pivot->Left = TempNode->Right;
    if(T->NullNode != TempNode->Right){
        TempNode->Right->Parent = Pivot;
    }
    TempNode->Right = Pivot;
    TempNode->Parent = Pivot->Parent;
    if(T->Root == Pivot){
        T->Root = TempNode;
    }
    else{
        if(Pivot == Pivot->Parent->Left){
            Pivot->Parent->Left = TempNode;
        }
        else{
            Pivot->Parent->Right = TempNode;
        }
    }
    Pivot->Parent = TempNode;
    
    return T;
}

Insert

---

红黑树的插入操作和BST也差不多，同样在插入以后需要像AVL树那样向上调整，但是红黑树因为每个节点都存在parent指针，所以向上调整可以通过迭代来实现，而不需要像AVL树那样要用递归回溯。红黑树向上调整的过程实际上就是不断将新插入的红节点向上移动，直至它的父节点为黑为止，这样就存在三种情况（之所以不存在其他情况，完全是由于红黑树的性质决定的）。并且红黑树的根节点和根节点的父节点的Color一定是Black，所以这个向上调整的过程就一定会停止，也就是最终一定能跳出循环，在跳出循环之后需要将根节点的Color赋值为Black。

以下三种情况均针对待调整节点在其祖父节点的左子树中时进行分析，若在右子树中时，做对称操作即可。

Case One

这种情况中,待调整节点是C节点，C节点的父节点B和父节点B的Sibling节点E的Color均为Red（需要注意的是这里C、D、E的左右子树可能为空，可能不为空，且A节点也可能不是根节点）。遇到这种情况时，将C节点的父节点B和父节点B的Sibling节点E的Color赋值为Black，并将C节点的祖父节点A赋值为Red，同时将待调整节点变为节点A。因为起初父节点的Color为Red，所以根据性质，C的祖父节点A的Color一定为Black，这样同时调整B和E为Black，可以使沿B和E至叶节点的路径上的Black节点数相同，且消除了B、C均为Red的情况，但是这样一来沿A至叶节点的路径上的Black节点数就增加了一个，因此将A赋值为Red，使得沿A至叶节点的路径上的Black节点数保持和调整前的数量一致，然而我们无法排除A的父节点的Color也是Red的情况，所以将待调整节点变为节点A，在下一次循环中继续调整。

Case Two

这种情况中，待调整节点是D节点，D节点的父节点B的Color是Red，但是父节点B的Sibling节点E的Color是Black，且D节点是其父节点B的右子节点。此时仅需要以B节点为Pivot做左旋即可，并将待调整节点变为B。在具体实现时还需要注意将记录父节点的变量FNode变为D节点，并进入Case Three。之所以要这样操作，是因为这里的操作仅仅针对两个Red节点，而对于Black节点的操作（例如C节点），起初沿B的左子节点、D的左（C节点）右子节点至叶节点的路径的Black节点数都是相同的，所以旋转操作中移动以C为根节点的子树后，沿B的子节点和D的子节点至叶节点的路径的Black节点数依然是相同的且保持不变。

Case Three

这种情况中，待调整节点是C节点，C节点的父节点B的Color是Red，但是父节点B的Sibling节点E的Color是Black，且C节点是其父节点B的左子节点。此时仅需要以C节点的祖父节点A作为Pivot做右旋即可，并将原先的父节点B的Color调整为Black，将原先的祖父节点A的Color调整为Red。之所以要这样操作，是因为起初沿C节点的左右子节点、沿D节点和E节点至叶节点的路径的Black节点数是相同的，所以在调整过后沿它们至叶节点的路径上的Black节点数依然是相同的且保持不变，而这样操作却可以通过交换颜色将一个Red节点移动到祖先节点的右子树中，消除了两个Red节点相连的情况，当然旋转后新的子树的根节点B要赋值为Black，以保持从子树的根节点（原先是A，现在是B）的路径的Black节点数保持和原来一样。这里要是Pivot是整棵红黑树的根节点，则需更新Root节点的值

Source Code

PtrRBT RBInsert(PtrRBT T, ElementType Val){
    PtrRBTNode TempNode = T->Root;
    PtrRBTNode NewNode = RBCreateNode(T, Val);
    
    if(NULL == TempNode){
        T->Root = NewNode;
        NewNode->Parent = T->NullNode;
    }
    else{
        while(T->NullNode != TempNode){
            if(Val < TempNode->Key){
                if(T->NullNode == TempNode->Left){
                    TempNode->Left = NewNode;
                    NewNode->Parent = TempNode;
                    break;
                }
                else{
                    TempNode = TempNode->Left;
                }
            }
            else{
                if(T->NullNode == TempNode->Right){
                    TempNode->Right = NewNode;
                    NewNode->Parent = TempNode;
                    break;
                }
                else{
                    TempNode = TempNode->Right;
                }
            }
        }
    }
    
    T = RBInsertFixUp(T, NewNode);
    
    return T;
}

PtrRBT RBInsertFixUp(PtrRBT T, PtrRBTNode CurrentNode){
    PtrRBTNode FNode, GNode, UNode;
    
    while(Red == CurrentNode->Parent->Color){
        FNode = CurrentNode->Parent;
        GNode = FNode->Parent;
        if(GNode->Left == FNode){
            UNode = GNode->Right;
            if(Red == FNode->Color&&Red == UNode->Color){
                FNode->Color = UNode->Color = Black;
                GNode->Color = Red;
                CurrentNode = GNode;
            }
            else{
                if(CurrentNode == FNode->Right){
                    T = RBLeftRotate(T, FNode);
                    CurrentNode = FNode;
                    FNode = CurrentNode->Parent;
                }
                FNode->Color = Black;
                GNode->Color = Red;
                T = RBRightRotate(T, GNode);
            }
        }
        else{
            UNode = GNode->Left;
            if(Red == FNode->Color&&Red == UNode->Color){
                FNode->Color = UNode->Color = Black;
                GNode->Color = Red;
                CurrentNode = GNode;
            }
            else{
                if(CurrentNode == FNode->Left){
                    T = RBRightRotate(T, FNode);
                    CurrentNode = FNode;
                    FNode = CurrentNode->Parent;
                }
                FNode->Color = Black;
                GNode->Color = Red;
                T = RBLeftRotate(T, GNode);
            }
        }
    }
    T->Root->Color = Black;
    
    return T;
}

5. 代码Git提交记录截图

在码云的项目中，依次选择统计-Commits历史-设置时间段，进行搜索并截图，如下图所示，需要出现学号、项目提交说明。请在码云中将你的昵称改为“学号-姓名”。