博客园作业-图

1.学习总结

1.1图的思维导图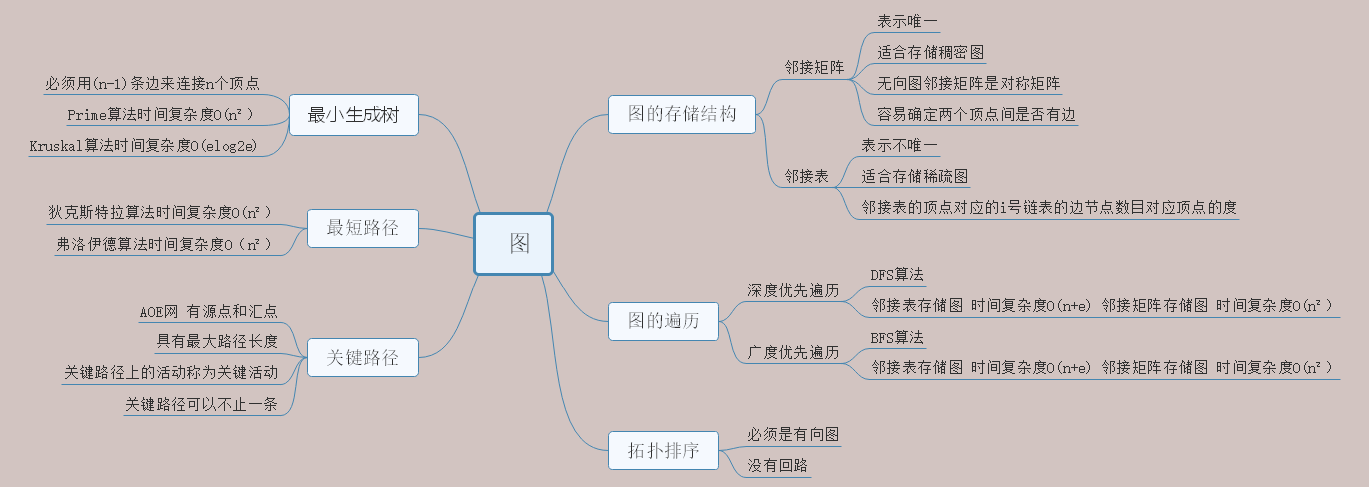

1.2图结构学习体会

图的存储结构：邻接表和邻接矩阵很容易理解，主要是代码实现这一方面有待加强；图的遍历：深度优先从初始定点开始访问其邻接顶点，然后再访问该顶点的未被访问过的邻接顶点，依此类推，代码上用邻接表来存储图；广度优先是从初始顶点开始访问，接着访问初始顶点的所有未被访问过的邻接点，然后按照邻接点的次序依次访问每一个顶点的未被访问过的点，依此类推，直到所有顶点被访问；对于最短路径和最小生成树概念以及算法过程都理解，但是代码上的掌握以及实际问题上的应用还是不熟悉，关键路径也是如此，拓扑排序相对简单点。总的来说，就是代码以及如何运用代码解决实际问题，这方面掌握得很薄弱

2.PTA实验作业

2.1.1实验题目一：7.2排座位

2.1.2代码设计思路

用一个邻接表来记录朋友关系，-1表示敌对，1表示朋友，0表示什么关系都没有，然后只要是朋友关系的就加入邻接表，遍历的时候采用DFS算法

2.1.3关键代码截图

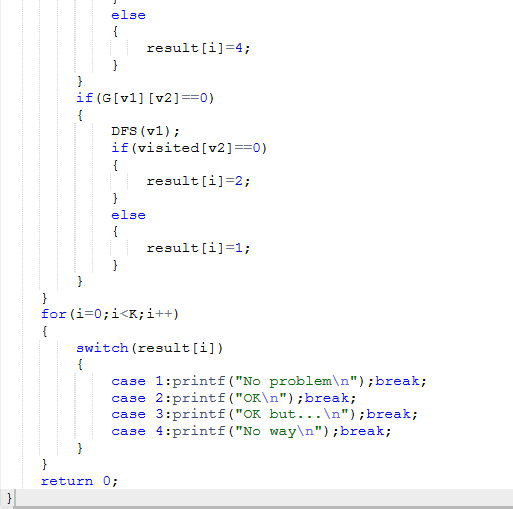
2.1.4PTA提交列表

 

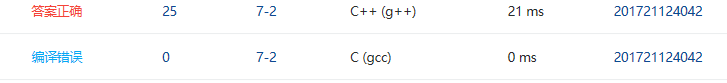
 刚开始自己的代码只能过一个测试点，后来换了一种方式，可以部分正确，然后自己的输出格式上也没有注意到换行，改正过之后就解决了

2.2.1实验题目二名称:7.4公路村村通

 2.2.2代码设计思路

每个村庄相当于树中的顶点，公路相当于树的边，每条公路的费用相当于边上的权值，因此求最小成本相当于求最小生成树

2.2.3关键代码截图

 

 

2.2.4PTA提交列表及其情况说明

 一开始自己只是写出来了Prime算法求出了最小生成树，但忘记了算权值，也就是修建公路的成本

2.3.1实验题目三 题目名称：7.7旅游规划

2.3.2代码设计思路

    这个题目的本质是dijstra 算法，不过要建立两个图，一个是路程图（不连通节点之间距离为INF），一个是费用图。运行dijstra 的时候分别更新最短距离和最少费用的数组。在更新最短距离的时候，条件为 lowcost[i]>=lowcost[k]+G[k][i]，也就是说如果新发现的路和原来的已发现的最短距离相同，要考虑相同的情况，单独距离相同的时候，判断费用是不是比原来的少，如果费用更少，则更新费用。此外，在更新最短距离的时候也要更新最短费用

2.3.3关键代码截图

2.3.4PTA提交列表及其情况说明

格式错误是因为自己没有注意到题目要求行尾不得有多余空格，然后答案错误是因为自己搞错了输出顺序

3.截图本周题目集PTA的最后排名

3.1PTA排名

3.2我的总分

4.阅读代码

struct data
{
    int b,lenth;
};
typedef struct node *Node;
struct node
{
    struct data Next[101];
    int Output,O;
    struct data From[101];
    int Input,I;
};

int TopSort(Node V,int n);
int* ImportantRode(Node,int,int );

int main()
{
    struct node V[101];
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++)
    {
        V[i].Input =0;
        V[i].Output =0;
    }
    while(m--)
    {
        int disk1,disk2,lenth;
        scanf("%d%d%d",&disk1,&disk2,&lenth);
        V[disk1].Next[++V[disk1].Output].b =disk2;
        V[disk1].Next[V[disk1].Output ].lenth=lenth;
        V[disk2].From[++V[disk2].Input].b=disk1;
        V[disk2].From[V[disk2].Input].lenth=lenth;
    }
    for(int i=1;i<=n;i++){
        V[i].I =V[i].Input ;
        V[i].O=V[i].Output ;
    }
    int Coast =TopSort(V,n);
    return 0;
}

int TopSort(Node V,int n)
{
    int Earliest[101]= {0};
    while(1)
    {
        int flag=0;
        for(int i=1; i<=n; i++)
        {
            if(0==V[i].Input)
            {
//              printf("{%d}",i);
                flag=1;
                for(int j=1; j<=V[i].Output ; j++)
                {
                    if(Earliest[V[i].Next[j].b]<Earliest[i]+V[i].Next[j].lenth)
                    {
                        Earliest[V[i].Next[j].b]=Earliest[i]+V[i].Next[j].lenth;
                    }
                    V[V[i].Next[j].b].Input-=1;
                }
                V[i].Input =-1;
            }
        }
        if(!flag)break;
    }
//  for(int i=0;i<n;i++){
//      printf("[%d|%d->%d]",V[i].Input,V[i].Output,Earliest[i] );
//  }
    int max=0,index;
    for(int i=1; i<=n; i++)
    {
        if(V[i].Input >0)
        {
            max=0;
            break;
        }
        if(Earliest[i]>max)
        {
            max=Earliest[i];
            index=i;
        }
    }
    printf("%d",max);
    if(max==0)return 0;
    int *Latest=ImportantRode(V,max,n);
    for(int i=1; i<=n; i++)
    {
//      printf("{%d,%d}",Earliest[i],Latest[i]);
        if(Latest[i]==Earliest[i])
        {
            for(int j=V[i].O; j>0; j--)
            {
                if(Latest[V[i].Next[j].b]==Latest[i]+V[i].Next[j].lenth )
                {
                    printf("\n%d->%d",i,V[i].Next[j].b);
                }
            }
        }
    }
    return max;
}
int* ImportantRode(Node V,int max,int n)
{
    int*Latest=(int*)malloc(sizeof(int)*101);
    for(int i=1; i<=n; i++)
    {
        Latest[i]=max;
    }
    while(1)
    {
        int flag=0;
        for(int i=1; i<=n; i++)
        {
            if(0==V[i].Output)
            {
                flag=1;
                for(int j=1; j<=V[i].I; j++)
                {
                    if(Latest[V[i].From[j].b]>Latest[i]-V[i].From[j].lenth)
                    {
                        Latest[V[i].From[j].b]=Latest[i]-V[i].From[j].lenth;
                    }
                    V[V[i].From[j].b].Output  -=1;
                }
                V[i].Output   =-1;
            }
        }
        if(!flag)break;
    }


return Latest;
}