排序算法小结
概述
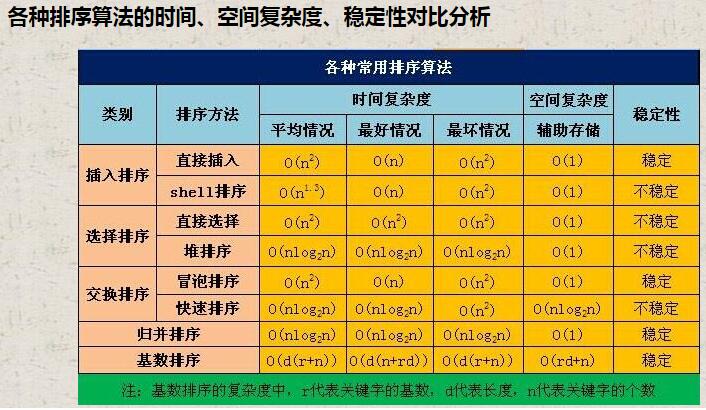
常见的排序算法都是比较排序,非比较排序包括计数排序、桶排序和基数排序,非比较排序对数据有要求,因为数据本身包含了定位特征,所有才能不通过比较来确定元素的位置。
比较排序的时间复杂度通常为O(n2)或者O(nlogn),比较排序的时间复杂度下界就是O(nlogn),而非比较排序的时间复杂度可以达到O(n),但是都需要额外的空间开销。
快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序。
当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O(n);而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O(n2);
原表是否有序,对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
排序的稳定性和复杂度
稳定性:若待排序的序列中,存在多个具有相同关键字的记录,经过排序, 这些记录的相对次序保持不变,则称该算法是稳定的;若经排序后,记录的相对 次序发生了改变,则称该算法是不稳定的。
稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。另外,如果排序算法稳定,可以避免多余的比较;
不稳定:
- 选择排序(selection sort)— O(n2)
- 快速排序(quicksort)— O(nlogn) 平均时间, O(n2) 最坏情况; 对于大的、乱序串列一般认为是最快的已知排序
- 堆排序 (heapsort)— O(nlogn)
- 选择排序(selection sort)— O(n2)
- 希尔排序 (shell sort)— O(nlogn)
- 基数排序(radix sort)— O(n·k); 需要 O(n) 额外存储空间 (K为特征个数)
稳定:
- 插入排序(insertion sort)— O(n2)
- 冒泡排序(bubble sort) — O(n2)
- 归并排序 (merge sort)— O(n log n); 需要 O(n) 额外存储空间
- 二叉树排序(Binary tree sort) — O(nlogn); 需要 O(n) 额外存储空间
- 计数排序 (counting sort) — O(n+k); 需要 O(n+k) 额外存储空间,k为序列中Max-Min+1
- 桶排序 (bucket sort)— O(n); 需要 O(k) 额外存储空间
选择排序算法准则
每种排序算法都各有优缺点。因此,在实用时需根据不同情况适当选用,甚至可以将多种方法结合起来使用。影响排序的因素有很多,平均时间复杂度低的算法并不一定就是最优的。相反,有时平均时间复杂度高的算法可能更适合某些特殊情况。同时,选择算法时还得考虑它的可读性,以利于软件的维护,一般而言,需要考虑的因素有以下四点:
- 待排序的记录数目n的大小;
- 记录本身数据量的大小,也就是记录中除关键字外的其他信息量的大小
- 关键字的结构及其分布情况
- 对排序稳定性的要求
- 当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序序。
快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
堆排序:如果内存空间允许且要求稳定性的
归并排序:它有一定数量的数据移动,所以我们可能过与插入排序组合,先获得一定长度的序列,然后再合并,在效率上将有所提高。
- 当n较大,内存空间允许,且要求稳定性 推荐 归并排序
- 当n较小,可采用直接插入或直接选择排序。
直接插入排序:当元素分布有序,直接插入排序将大大减少比较次数和移动记录的次数。
直接选择排序 :元素分布有序,如果不要求稳定性,选择直接选择排序
- 一般不使用或不直接使用传统的冒泡排序。
- 基数排序它是一种稳定的排序算法,但有一定的局限性
关键字可分解
记录的关键字位数较少,如果密集更好
如果是数字时,最好是无符号的,否则将增加相应的映射复杂度,可先将其正负分开排序。
各种排序
插入排序法
对于前面i个已经升序排好的部分,取挨着的第i+1个,和第i个比较,如果大于的话,第i+1个排序完成;如果是小于,则继续与第i-1个进行比较,直到遇到比其大的,在其后面插入,完成第i+1排序。继续进行第i+2个排序
插入排序基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。插入排序的基本思想是:每步将一个待排序的纪录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。
当待排序的数据基本有序时,插入排序的效率比较高,只需要进行很少的数据移动。所以插入排序是稳定的。
void insert_Sort(int[] array)
{
for (int i = 1; i < array.Length; i++)
{
int data = array[i];
for (int j = i - 1; j >= 0; j--)
{
if (data < array[j])
{
array[j + 1] = array[j];
array[j] = data;
}
else
{
array[j + 1] = data;
break;
}
}
}
}
void insert_Sort2(int[] array)
{
for (int i = 1; i < array.Length; i++)
{
int data = array[i];
int j = i - 1;
for (;j >= 0 && (data < array[j]); j--)
{
array[j + 1] = array[j];
}
array[j + 1] = data;
}
}
冒泡排序法
冒泡排序法是相邻的两个进行比较,大的排在后面,滚动式向后移动比较,经过第一轮比较和移动,最大元素会排在最后面,第二轮后,次大的位于倒数第二个,依次进行。
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端。
void bubble_Sort(int[] array)
{
for (int i = 0; i < array.Length-1; i++)
{
for (int j = 1; j < array.Length-i; j++)
{
if (array[j] < array[j-1])
{
int tmp = array[j];
array[j] = array[j-1];
array[j-1] = tmp;
}
}
}
}
优化一
如果某一轮两两比较中没有任何元素交换,这说明已经都排好序了,算法结束,可以使用一个Flag做标记,默认为false,如果发生交互则置为true,每轮结束时检测Flag,如果为true则继续,如果为false则返回。
void bubble_Sort_Optimize1(int[] array)
{
bool flag = false;
for (int i = 0; i < array.Length - 1;flag = false, i++)
{
for (int j = 1; j < array.Length - i; j++)
{
if (array[j] < array[j - 1])
{
int tmp = array[j];
array[j] = array[j - 1];
array[j - 1] = tmp;
flag = true;
}
}
if (!flag)
{
break;
}
}
}
优化二
某一轮结束位置为j,但是这一轮的最后一次交换发生在lastSwap的位置,则lastSwap到j之间是排好序的,下一轮的结束点就不必是j--了,而直接到lastSwap即可,代码如下:
void bubble_Sort_Optimize2(int[] array)
{
int lastSwap = array.Length;
for (int i = 0; i < array.Length - 1; i++)
{
int j = 1;
for (; j < lastSwap; j++)
{
if (array[j] < array[j - 1])
{
int tmp = array[j];
array[j] = array[j - 1];
array[j - 1] = tmp;
}
}
lastSwap = j-1;
}
}
选择排序法
遍历数组,遍历到i时,a0,a1...ai-1是已经排好序的,然后从i到n选择出最小的,记录下位置,如果不是第i个,则和第i个元素交换。此时第i个元素可能会排到相等元素之后,造成排序的不稳定。
void selection_Sort(int[] array)
{
for (int i = 0; i < array.Length - 1; i++)
{
int pos = i;
for (int j = i + 1; j < array.Length; j++)
if (array[pos] > array[j])
{
pos = j;
}
if (pos != i)
{
int tmp = array[i];
array[i] = array[pos];
array[pos] = tmp;
}
}
}
快速排序法
快速排序(Quicksort)是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。其实现时通过递归实现的(也可以不用递归)
该方法的基本思想是:
- 先从数列中取出一个数作为基准数。
- 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边
- 再对左右区间重复第二步,直到各区间只有一个数。

void QuickSort(int[] R, int low, int high)
{
int pivotLoc = 0;
if (low < high)
{
pivotLoc = Partition(R, low, high);
QuickSort(R, low, pivotLoc - 1);
QuickSort(R, pivotLoc + 1, high);
}
}
int Partition(int[] R, int low, int high)
{
int temp = R[low];
while (low < high)
{
while (low < high && temp <= R[high])
{
high--;
}
R[low] = R[high];
while (low < high && temp >= R[low])
{
low++;
}
R[high] = R[low];
}
R[low] = temp;
return low;
}
堆排序法
堆排序是一种树形选择排序,是对直接选择排序的改进。
我们来看看什么是堆(heap):
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树(Complete Binary Tree)。
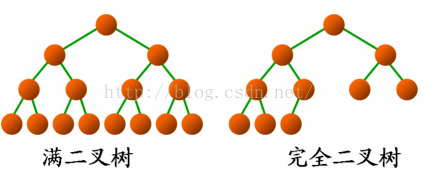
完全二叉树是由满二叉树(Full Binary Tree)而引出来的。除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树称为满二叉树。
如果除最后一层外,每一层上的节点数均达到最大值;在最后一层上只缺少右边的若干结点,这样的二叉树被称为完全二叉树。
堆排序是把数组看作堆,堆排序的第一步是建堆,然后是取堆顶元素然后调整堆。建堆的过程是自底向上不断调整达成的,这样当调整某个结点时,其左节点和右结点已经是满足条件的,此时如果两个子结点不需要动,则整个子树不需要动,如果调整,则父结点交换到子结点位置,再以此结点继续调整。
初始化堆
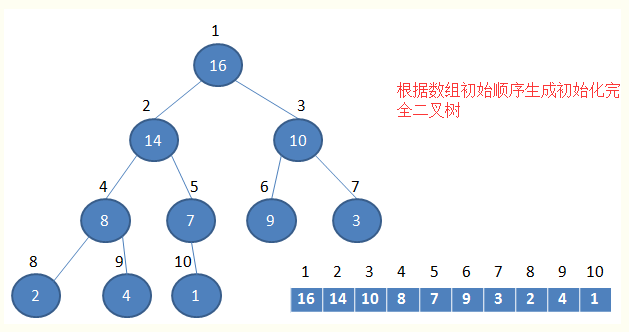
当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆
调整堆成最大堆
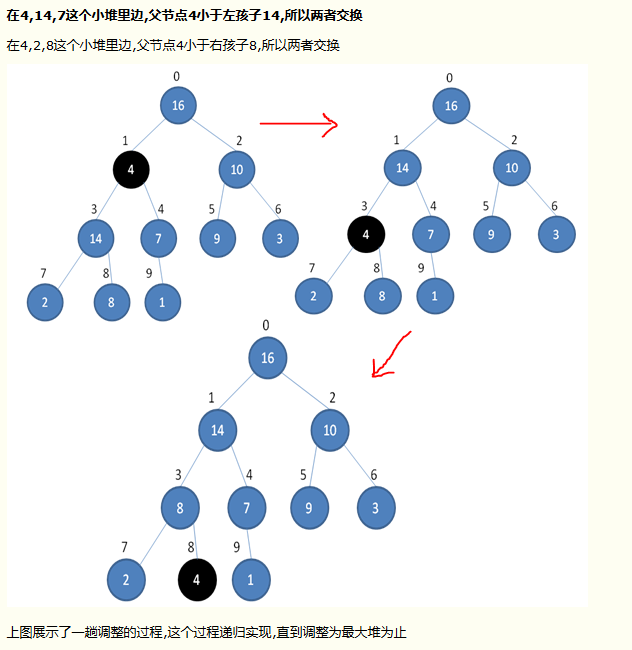
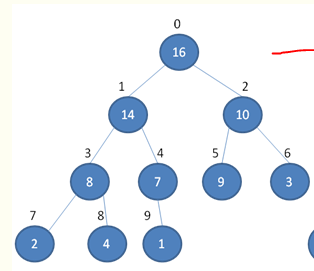
堆排序
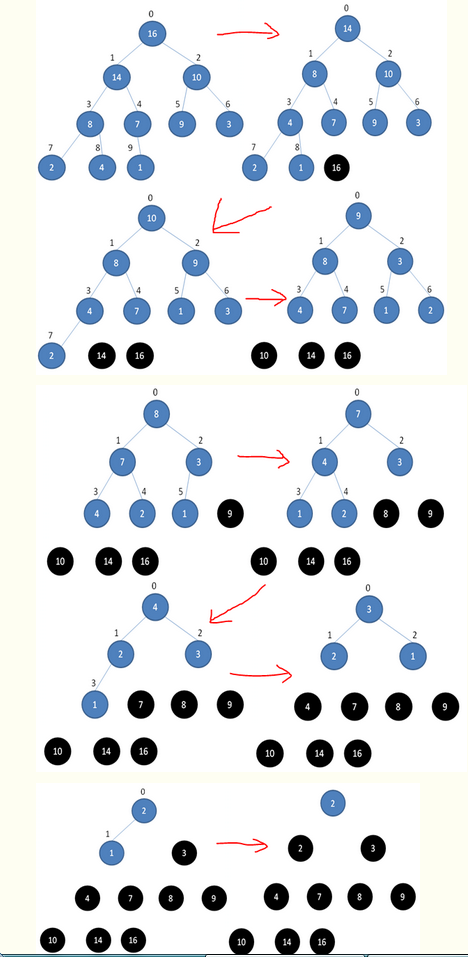
- 堆排序就是把堆顶的最大数取出,如上16删掉
- 将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现
- 剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束
//堆排序算法(传递待排数组名,即:数组的地址。故形参数组的各种操作反应到实参数组上)
private static void HeapSortFunction(int[] array)
{
try
{
BuildMaxHeap(array); //创建大顶推(初始状态看做:整体无序)
for (int i = array.Length - 1; i > 0; i--)
{
Swap(ref array[0], ref array[i]); //将堆顶元素依次与无序区的最后一位交换(使堆顶元素进入有序区)
MaxHeapify(array, 0, i); //重新将无序区调整为大顶堆
}
}
catch (Exception ex)
{ }
}
// 创建大顶推(根节点大于左右子节点)
//array待排数组
private static void BuildMaxHeap(int[] array)
{
try
{
//根据大顶堆的性质可知:数组的前半段的元素为根节点,其余元素都为叶节点
for (int i = array.Length / 2 - 1; i >= 0; i--) //从最底层的最后一个根节点开始进行大顶推的调整
{
MaxHeapify(array, i, array.Length); //调整大顶堆
}
}
catch (Exception ex)
{ }
}
// 大顶推的调整过程
//array待调整的数组
//currentIndex待调整元素在数组中的位置(即:根节点)
//heapSize堆中所有元素的个数
private static void MaxHeapify(int[] array, int currentIndex, int heapSize)
{
try
{
int left = 2 * currentIndex + 1; //左子节点在数组中的位置
int right = 2 * currentIndex + 2; //右子节点在数组中的位置
int large = currentIndex; //记录此根节点、左子节点、右子节点 三者中最大值的位置
if (left < heapSize && array[left] > array[large]) //与左子节点进行比较
{
large = left;
}
if (right < heapSize && array[right] > array[large]) //与右子节点进行比较
{
large = right;
}
if (currentIndex != large) //如果 currentIndex != large 则表明 large 发生变化(即:左右子节点中有大于根节点的情况)
{
Swap(ref array[currentIndex], ref array[large]); //将左右节点中的大者与根节点进行交换(即:实现局部大顶堆)
MaxHeapify(array, large, heapSize); //以上次调整动作的large位置(为此次调整的根节点位置),进行递归调整
}
}
catch (Exception ex)
{ }
}
// 交换函数
//a:元素a
//b:元素b
private static void Swap(ref int a, ref int b)
{
int temp = 0;
temp = a;
a = b;
b = temp;
}
堆排序的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n2)的时间复杂度了。空间复杂度上,它只有一个用来交换的暂存单元,也非常的不错。不过由于记录的比较与交换是跳跃式进行,因此堆排序是一种不稳定的排序方法。
归并排序
归并排序(Merge Sort)是利用"归并"技术来进行排序。归并是指将若干个已排序的子文件合并成一个有序的文件。
分治法的三个步骤
- 分解:将当前区间一分为二,即求分裂点
- 求解:递归地对两个子区间R[low..mid]和R[mid+1..high]进行归并排序
- 组合:将已排序的两个子区间R[low..mid]和R[mid+1..high]归并为一个有序的区间R[low..high]
- 递归的终结条件:子区间长度为1(一个记录自然有序)。

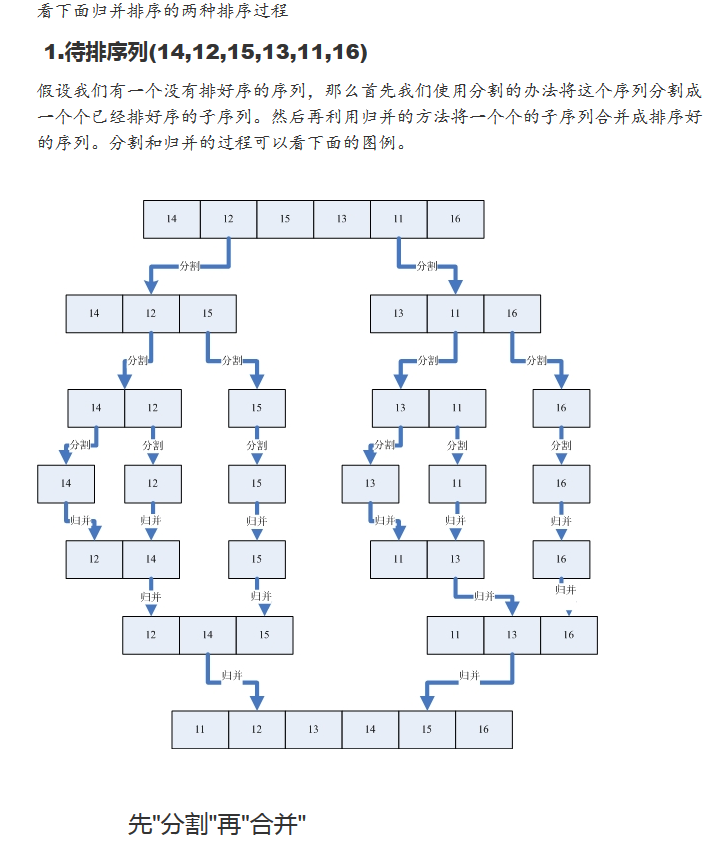
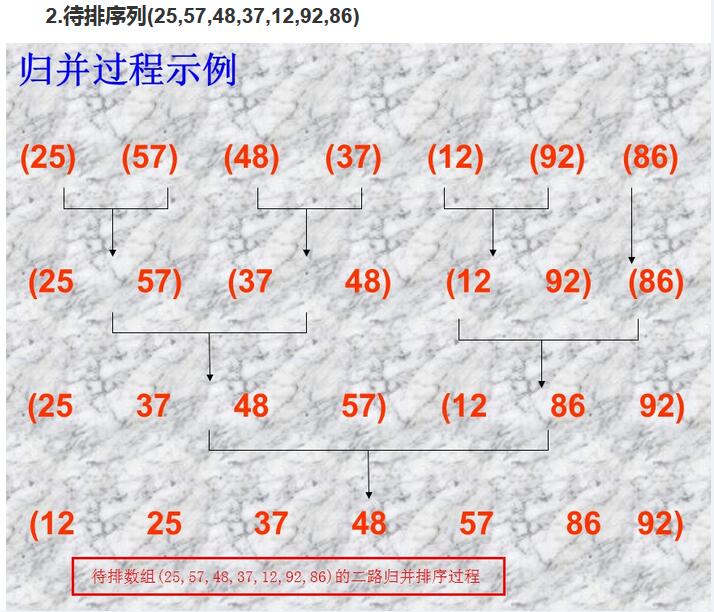
归并排序是采用分治法(Divide and Conquer)的一个非常典型的应用。首先考虑下如何将将二个有序数列合并。这个非常简单,只要从比较二个数列的第一个数,谁小就先取谁,取了后就在对应数列中删除这个数。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。这需要将待排序序列中的所有记录扫描一遍,因此耗费O(n)时间,而由完全二叉树的深度可知,整个归并排序需要进行.logn.次,因此,总的时间复杂度为O(nlogn)。
归并算法需要两两比较,不存在跳跃,因此归并排序是一种稳定的排序算法。
//归并排序(目标数组,子表的起始位置,子表的终止位置)
private static void MergeSortFunction(int[] array, int first, int last)
{
try
{
if (first < last) //子表的长度大于1,则进入下面的递归处理
{
int mid = (first + last) / 2; //子表划分的位置
MergeSortFunction(array, first, mid); //对划分出来的左侧子表进行递归划分
MergeSortFunction(array, mid + 1, last); //对划分出来的右侧子表进行递归划分
MergeSortCore(array, first, mid, last); //对左右子表进行有序的整合(归并排序的核心部分)
}
}
catch (Exception ex)
{ }
}
//归并排序的核心部分:将两个有序的左右子表(以mid区分),合并成一个有序的表
private static void MergeSortCore(int[] array, int first, int mid, int last)
{
try
{
int indexA = first; //左侧子表的起始位置
int indexB = mid + 1; //右侧子表的起始位置
int[] temp = new int[last + 1]; //声明数组(暂存左右子表的所有有序数列):长度等于左右子表的长度之和。
int tempIndex = 0;
while (indexA <= mid && indexB <= last) //进行左右子表的遍历,如果其中有一个子表遍历完,则跳出循环
{
if (array[indexA] <= array[indexB]) //此时左子表的数 <= 右子表的数
{
temp[tempIndex++] = array[indexA++]; //将左子表的数放入暂存数组中,遍历左子表下标++
}
else//此时左子表的数 > 右子表的数
{
temp[tempIndex++] = array[indexB++]; //将右子表的数放入暂存数组中,遍历右子表下标++
}
}
//有一侧子表遍历完后,跳出循环,将另外一侧子表剩下的数一次放入暂存数组中(有序)
while (indexA <= mid)
{
temp[tempIndex++] = array[indexA++];
}
while (indexB <= last)
{
temp[tempIndex++] = array[indexB++];
}
//将暂存数组中有序的数列写入目标数组的制定位置,使进行归并的数组段有序
tempIndex = 0;
for (int i = first; i <= last; i++)
{
array[i] = temp[tempIndex++];
}
}
catch (Exception ex)
{ }
}
希尔排序
希尔排序的实质就是分组插入排序,该方法又称缩小增量排序
希尔排序的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
希尔排序是对插入排序的优化,基于以下两个认识:1. 数据量较小时插入排序速度较快,因为n和n2差距很小;2. 数据基本有序时插入排序效率很高,因为比较和移动的数据量少。

void shell_Sort(int[] array)
{
int d, i, j, temp; //d为增量
for (d = array.Length / 2; d >= 1; d = d / 2) //增量递减到1使完成排序
{
for (i = d; i < array.Length; i++) //插入排序的一轮
{
temp = array[i];
for (j = i - d; (j >= 0) && (array[j] > temp); j = j - d)
{
array[j + d] = array[j];
}
array[j + d] = temp;
}
}
}
//下为插入法 可以看出是把里面的1变成了增量d
for (int i = 1; i < array.Length; i++)
{
int data = array[i];
int j = i - 1;
for (;j >= 0 && (data < array[j]); j--)
{
array[j + 1] = array[j];
}
array[j + 1] = data;
}
计数排序法
计数排序的思想是,考虑待排序数组中的某一个元素a,如果数组中比a小的元素有s个,那么a在最终排好序的数组中的位置将会是s+1,如何知道比a小的元素有多少个,肯定不是通过比较去觉得,而是通过数字本身的属性,即累加数组中最小值到a之间的每个数字出现的次数(未出现则为0),而每个数字出现的次数可以通过扫描一遍数组获得。
计数排序要求待排序的数组元素都是 整数,有很多地方都要去是0-K的正整数,其实负整数也可以通过都加一个偏移量解决的。
计数排序适合数据分布集中的排序,如果数据太分散,会造成空间的大量浪费
计数排序的步骤:
- 找出待排序的数组中最大和最小的元素(计数数组C的长度为max-min+1,其中位置0存放min,依次填充到最后一个位置存放max)
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1(反向填充是为了保证稳定性)
桶排序法
假设有一组长度为N的待排关键字序列K[1....n]。首先将这个序列划分成M个的子区间(桶) 。然后基于某种映射函数 ,将待排序列的关键字k映射到第i个桶中(即桶数组B的下标 i) ,那么该关键字k就作为B[i]中的元素(每个桶B[i]都是一组大小为N/M的序列)。接着对每个桶B[i]中的所有元素进行比较排序(可以使用快排)。然后依次枚举输出B[0]....B[M]中的全部内容即是一个有序序列。
桶排序利用函数的映射关系,减少了计划所有的比较操作,是一种Hash的思想,可以用在海量数据处理中。
计数排序也可以看作是桶排序的特例,数组关键字范围为N,划分为N个桶。
基数排序法
是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数
它是这样实现的:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
基数排序也可以看作一种桶排序,不断的使用不同的标准对数据划分到桶中,最终实现有序。基数排序的思想是对数据选择多种基数,对每一种基数依次使用桶排序。
基数排序的步骤:以整数为例,将整数按十进制位划分,从低位到高位执行以下过程。
- 从个位开始,根据0~9的值将数据分到10个桶桶,例如12会划分到2号桶中。
- 将0~9的10个桶中的数据顺序放回到数组中。
- 重复上述过程,一直到最高位。
- 上述方法称为LSD(Least significant digital),还可以从高位到低位,称为MSD。LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好。MSD的方式与LSD相反,是由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。

public int[] RadixSort(int[] ArrayToSort, int digit)
{
//low to high digit
for (int k = 1; k <= digit; k++)
{
//temp array to store the sort result inside digit
int[] tmpArray = new int[ArrayToSort.Length];
//temp array for countingsort
int[] tmpCountingSortArray = new int[10] { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
//CountingSort
for (int i = 0; i < ArrayToSort.Length; i++)
{
//split the specified digit from the element
int tmpSplitDigit = ArrayToSort[i] / (int)Math.Pow(10, k - 1) - (ArrayToSort[i] / (int)Math.Pow(10, k)) * 10;
tmpCountingSortArray[tmpSplitDigit] += 1;
}
for (int m = 1; m < 10; m++)
{
tmpCountingSortArray[m] += tmpCountingSortArray[m - 1];
}
//output the value to result
for (int n = ArrayToSort.Length - 1; n >= 0; n--)
{
int tmpSplitDigit = ArrayToSort[n] / (int)Math.Pow(10, k - 1) - (ArrayToSort[n] / (int)Math.Pow(10, k)) * 10;
tmpArray[tmpCountingSortArray[tmpSplitDigit] - 1] = ArrayToSort[n];
tmpCountingSortArray[tmpSplitDigit] -= 1;
}
//copy the digit-inside sort result to source array
for (int p = 0; p < ArrayToSort.Length; p++)
{
ArrayToSort[p] = tmpArray[p];
}
}
return ArrayToSort;
}

